bzoj 1010 玩具装箱toy -斜率优化

Posted 2020-08-29 阿波罗2003

　　P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压
缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为1...N的N件玩具，第i件玩具经过
压缩后变成一维长度为Ci.为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容
器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一
个容器中，那么容器的长度将为 x=j-i+Sigma(Ck) i<=K<=j 制作容器的费用与容器的长度有关，根据教授研究，
如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容
器，甚至超过L。但他希望费用最小.

Input

　　第一行输入两个整数N，L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7

Output

　　输出最小费用

Sample Input

5 4
3
4
2
1
4

Sample Output

1

---

　　先推出普通dp的方程　　　　f[i] = min{f[j] + (sum[i] - sum[j] + i - j - 1 - L)²}

　　这方程明显是O(n²)级别的，再看看这卖萌的数据范围，不用质疑，铁定超时。还是来考虑一下优化(例如斜率优化)吧。由于这方程长得太丑了，于是决定简化一下

　　设S(i) = sum[i] + i，C = L + 1

　　于是方程变成了这样　　　　f[i] = min{f[j] + (S(i) - S（j） - C)²}

　　现在假设在状态i之前有两个可以转移到i的两个状态j, k(j < k),现在使j比k更优，那么它要满足

f[j] + (S(i) - S（j） - C)² < f[k] + (S(i) - S（k） - C)² 

　　看平方不爽，而且无法化简，果断完全平方公式拆掉

f[j] + [S(i) - (S（j） + C)]² < f[k] + [S(i) - (S（k） + C)]²

f[j] + (S(j) + C)² - 2S(i)[S(j) + C] < f[j] + (S(k) + C)² - 2S(i)[S(k) + C]

　　（其实可以一起拆掉，只不过中途有些地方可以直接"抵消"）继续"拆"括号，移项

f[j] + S(j)² + 2S(j)C - 2S(i)[S(j) - S(k)] < f[k] + S(k)² + 2S(k)C

　　继续，右边只留一个和i有关的单项式

(f[j] + S(j)² + 2S(j)C) - (f[k] + S(k)² + 2S(k)C) < 2S(i)[S(j) - S(k)]

　　继续移项，右边只留和i有关的式子

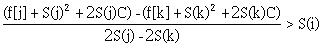
 　 注意，S(i)是单调递增，所以S(j) - S(k) < 0，移项的时候不等号方向相反，于是我们愉快地得到了斜率方程（干什么？斜率优化去掉一个n）。

　　对于状态i，用(f[i] + S(i)² + 2S(i)C)作纵坐标，2S(i)作横坐标，删掉上凸点，维护一条斜率递增的折线即可。

Code

 

  1 /**
  2  * bzoj
  3  * Problem#1010
  4  * Accepted
  5  * Time:172ms
  6  * Memory:2468k
  7  */
  8 #include<iostream>
  9 #include<sstream>
 10 #include<cstdio>
 11 #include<cmath>
 12 #include<cstdlib>
 13 #include<cstring>
 14 #include<cctype>
 15 #include<queue>
 16 #include<set>
 17 #include<map>
 18 #include<stack>
 19 #include<vector>
 20 #include<algorithm>
 21 #ifdef    WIN32
 22 #define    AUTO "%I64d"
 23 #else
 24 #define AUTO "%lld"
 25 #endif
 26 using namespace std;
 27 typedef bool boolean;
 28 #define smin(a, b) (a) = min((a), (b))
 29 #define smax(a, b) (a) = max((a), (b))
 30 template<typename T>
 31 inline void readInteger(T& u){
 32     char x;
 33     int aFlag = 1;
 34     while(!isdigit((x = getchar())) && x != \'-\');
 35     if(x == \'-\'){
 36         aFlag = -1;
 37         x = getchar();
 38     }
 39     for(u = x - \'0\'; isdigit((x = getchar())); u = u * 10 + x - \'0\');
 40     ungetc(x, stdin);
 41     u *= aFlag;
 42 }
 43 
 44 template<typename T>
 45 class IndexedDeque{
 46     public:
 47         T* list;
 48         int pfront;
 49         int prear;
 50         IndexedDeque():list(NULL), pfront(0), prear(0){        }
 51         IndexedDeque(int size):pfront(0), prear(0){
 52             list = new T[size];
 53         }
 54         void push_front(T x){    list[--pfront] = x;        }
 55         void push_back(T x)    {    list[prear++] = x;        }
 56         void pop_front()    {    ++pfront;                }
 57         void pop_back()        {    --prear;                }
 58         T     front()        {    return list[pfront];    }
 59         T     rear()            {    return list[prear - 1];        }
 60         T& operator [](int pos){            return list[pfront + pos];        }
 61         int size()            {    return prear - pfront;    }
 62 };
 63 
 64 int n, L;
 65 long long* f;
 66 long long* sum;
 67 int C;
 68 
 69 #define        s(i)    (sum[(i)] + (i))
 70 #define        y_pos(i)    (f[(i)] + pow2(s(i)) + 2 * C * s(i))
 71 #define        x_pos(i)    (2 * s(i))
 72 
 73 template<typename T>
 74 inline long long pow2(T x){    return x * x;    }
 75 inline long long segsum(int from, int end){    return sum[end] - sum[from - 1];    }
 76 inline double slope(long long x1, long long y1, long long x2, long long y2){    return (y2 - y1) * 1.0 / (x2 - x1); }
 77 inline double slope(int j, int k){    return slope(x_pos(j), y_pos(j), x_pos(k), y_pos(k));    }
 78 inline double cmpSlope(int j, int k, int i){    return slope(x_pos(j), y_pos(j), x_pos(k), y_pos(k)) - s(i);    }
 79 
 80 inline void init(){
 81     readInteger(n);
 82     readInteger(L);
 83     sum = new long long[(const int)(n + 1)];
 84     f = new long long[(const int)(n + 1)];
 85     sum[0] = 0;
 86     for(int i = 1, a; i <= n; i++){
 87         readInteger(a);
 88         sum[i] = sum[i - 1] + a;
 89     }
 90 }
 91 
 92 IndexedDeque<int> que;
 93 inline void solve(){
 94     C = L + 1;
 95     que = IndexedDeque<int>(2 * n);
 96     que.push_back(0);
 97     f[0] = 0;
 98     for(int i = 1; i <= n; i++){
 99         while(que.size() > 1 && cmpSlope(que[0], que[1], i) <= 0) que.pop_front();
100         int p = que.front();
101         f[i] = f[p] + pow2(segsum(p + 1, i) + i - p - C);
102         while(que.size() > 1 && slope(que[que.size() - 2], que[que.size() - 1]) >= slope(que[que.size() - 1], i))    que.pop_back();
103         que.push_back(i);
104     }
105     printf("%lld\\n", f[n]);
106 }
107 
108 int main(){
109     init();
110     solve();
111     return 0;
112 }

---

(2017-2-2,更正之前贴错的代码

 2017-5-6,更正打错的内容)