有重复元素的全排列

Posted 2023-04-03

这是我的代码： #include <stdio.h> #include "stdlib.h" inline void Swap(char& a, char& b) // 交换a和b char temp = a; a = b; b = temp; void Perm(char list[], int k, int m) //生成list [k：m ]的所有排列方式 int i; if (k == m) //输出一个排列方式 for (i = 0; i <= m; i++) putchar(list[i]); putchar('\n'); 为什么输出结果不是Sample Input 输入 4 aacc 输出 aacc acac acca caac caca ccaa 6
#include <stdio.h>
#include "stdlib.h"
inline void Swap(char& a, char& b)
// 交换a和b
char temp = a;
a = b;
b = temp;


void Perm(char list[], int k, int m)
//生成list [k：m ]的所有排列方式
int i;
if (k == m) //输出一个排列方式
for (i = 0; i <= m; i++)
putchar(list[i]);
putchar('\n');

else // list[k：m ]有多个排列方式
// 递归地产生这些排列方式
for (i=k; i <= m; i++)
if(list[k]!=list[i])
Swap (list[k], list[i]);
Perm (list, k+1, m);
Swap (list [k], list [i]);


int main()
int i,k,j;

scanf("%d",&i);

char s[i];
for(k=0;k<i;k++)
scanf("%c",&s[k]);
// char s[]="abc";

Perm(s, 0,j);

system("pause");

return 0;

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
// 字符串最大长度
#define MAX_STRING_LENGTH 50
// 全排列顺序。TRUE:按字母序升序；FALSE:按字母序降序。
#define PERMUTATION_ASSCENDING_ORDER TRUE
// qsort 函数使用的比较函数
int compare(const void *a, const void *b)

return PERMUTATION_ASSCENDING_ORDER
? *((char*)a) - *((char*)b)
: *((char*)b) - *((char*)a);

/*
无重复全排序。
参数：
str 要进行无重复全排序的字符串。
字符串内字符必须已经排序过（升序或降序都可以）

isUsed 如果 isUsed[i] = TRUE 表示 str[i] 已经加入当前排列中

p 当前排列中已经存在的字符数

buffer 当前的排列。
buffer[0]~buffer[p-1] 是 str 中已经加入排列的字符。

返回：
无重复全排序的总数。
*/
int Perm(char str[],int isUsed[],int p ,char buffer[])

int len=strlen(str),i,j,total=0;

if(p == len)
// 输出一个全排列
printf("%s\n",buffer);
return 1;


for(i=0;i<len;i++)

if(!isUsed[i])

// 查询当前字符的后面，是否已经有和当前字符相同的字母加入了全排序中。
for(j=i+1;j<len;j++)
if(str[i]==str[j] && isUsed[j])
break;

if(j == len)
// 当前字符的后面，没有和当前字符相同的字母加入了全排序中。
// 当前字符可以加入全排序

isUsed[i] = TRUE;
buffer[p] = str[i];
total += Perm(str,isUsed,p+1,buffer);
isUsed[i] = FALSE;



return total;


int main(int argc, char *argv[])

char str[MAX_STRING_LENGTH]="aacc";
char buffer[MAX_STRING_LENGTH]=0;
int isUsed[MAX_STRING_LENGTH]=0;

while(scanf("%s",str)!=EOF)

// 先按字母序排序
qsort(str,strlen(str),sizeof(str[0]),compare);
// 全排列
printf("Total %d\n\n",Perm(str,isUsed,0,buffer));

return 0;
参考技术A 代码不全！~ 没有主函数。
把函数改成:
void Perm(char list[], int k, int m)
//生成list [k：m ]的所有排列方式
int i;
if (k == m) //输出一个排列方式
for (i = 0; i <=m; i++)
putchar(list[i]);
putchar('\n');

else // list[k：m ]有多个排列方式
// 递归地产生这些排列方式
for (int t,i=k; i <=m; i++)
//查找以前是否出现过
for(t=k;t<i;t++)

if(list[t]==list[i])
break;

if(t==i)

Swap (list[k], list[i]);
Perm (list, k+1, m);
Swap (list [k], list [i]);




另外主函数测试可写成：
int main() int i,k,j;
//scanf("%d",&i);
//for(k=0;k<i;k++)
//scanf("%c",&s[k]);
char s[]="aacc";

Perm(s, 0,4-1);
system("pause");
return 0;

递归与回溯14：排列问题，有重复元素的全排列

LeetCode47，与前面的不同是给定的数字序列可能有重复，请你返回全排列结果。例如：

输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

为了方便去重一定要对元素经行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

我以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

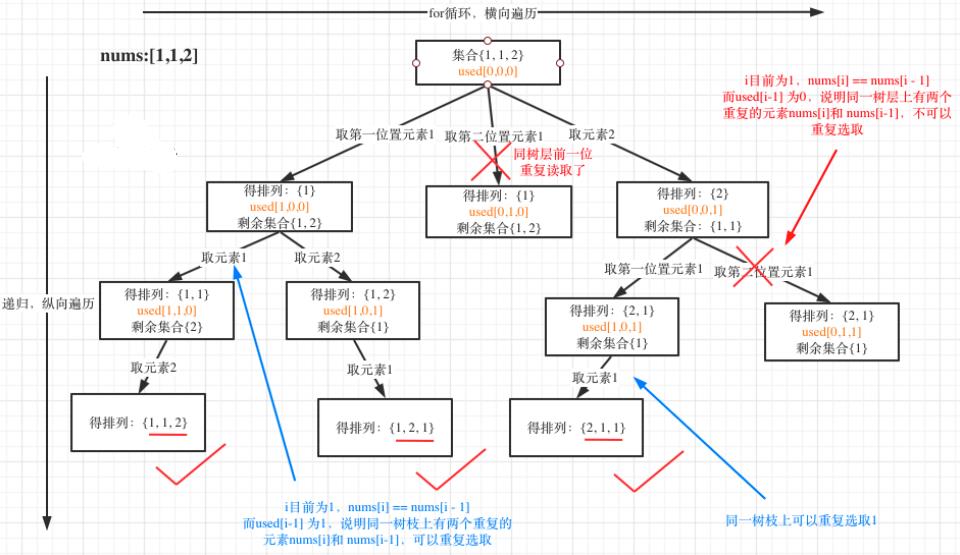
 图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

class Solution 
    //存放结果
    List<List<Integer>> result = new ArrayList<>();
    //暂存结果
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> permuteUnique(int[] nums) 
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        Arrays.sort(nums);
        backTrack(nums, used);
        return result;
    

    private void backTrack(int[] nums, boolean[] used) 
        if (path.size() == nums.length) 
            result.add(new ArrayList<>(path));
            return;
        
        for (int i = 0; i < nums.length; i++) 
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀层nums[i - 1]使⽤过
            // 如果同⼀层nums[i - 1]使⽤过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) 
                continue;
            
            //如果同⼀树⽀nums[i]没使⽤过开始处理
            if (used[i] == false) 
                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树支重复使用
                path.add(nums[i]);
                backTrack(nums, used);
                path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
                used[i] = false;//回溯