如何计算时间复杂度

Posted 2023-04-02

1、先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

2、举例

for（i=1;i<=n;++i）

 for(j=1;j<=n;++j) 

 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n的平方次

for(k=1;k<=n;++k)

c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n的三次方次  

则有 T（n）= n的平方+n的三次方，根据上面括号里的同数量级，我们可以确定 n的三次方为T（n）的同数量级

则有f（n）= n的三次方，然后根据T（n）/f（n）求极限可得到常数c

则该算法的 时间复杂度：T（n）=O（n的三次方）

扩展资料

分类

按数量级递增排列，常见的时间复杂度有：常数阶O(1),对数阶O( 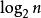 ),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n^2)，立方阶O(n^3),...，

k次方阶O(n^k),指数阶O(2^n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

关于对其的理解

《数据结构（C语言版）》 ------严蔚敏 吴伟民编著 第15页有句话“整个算法的执行时间与基本操作重复执行的次数成正比。”

基本操作重复执行的次数是问题规模n的某个函数f(n)，于是算法的时间量度可以记为：T(n) = O(f(n))

如果按照这么推断，T(n)应该表示的是算法的时间量度，也就是算法执行的时间。

而该页对“语句频度”也有定义：指的是该语句重复执行的次数。

如果是基本操作所在语句重复执行的次数，那么就该是f(n)。

上边的n都表示的问题规模。

参考资料：百度百科-时间复杂度

参考技术A 计算方法
1. 一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f(n)，因此，算法的时间复杂度记做：T(n)=O(f(n))
分析：随着模块n的增大，算法执行的时间的增长率和 f(n) 的增长率成正比，所以 f(n) 越小，算法的时间复杂度越低，算法的效率越高。
2. 在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出 T(n) 的同数量级（它的同数量级有以下：1，log(2)n，n，n log(2)n ，n的平方，n的三次方，2的n次方，n!），找出后，f(n) = 该数量级，若 T(n)/f(n) 求极限可得到一常数c，则时间复杂度T(n) = O(f(n))
例：算法：

1
2
3
4
5
6
7
8
9

for(i=1;i<=n;++i)

for(j=1;j<=n;++j)

c[i][j]=0;//该步骤属于基本操作执行次数：n的平方次
for(k=1;k<=n;++k)
c[i][j]+=a[i][k]*b[k][j];//该步骤属于基本操作执行次数：n的三次方次



则有 T(n) = n 的平方+n的三次方，根据上面括号里的同数量级，我们可以确定 n的三次方 为T（n）的同数量级
则有 f(n) = n的三次方，然后根据 T(n)/f(n) 求极限可得到常数c
则该算法的时间复杂度：T(n) = O(n^3) 注：n^3即是n的3次方。
3.在pascal中比较容易理解，容易计算的方法是：看看有几重for循环，只有一重则时间复杂度为O(n)，二重则为O(n^2)，依此类推，如果有二分则为O(logn)，二分例如快速幂、二分查找，如果一个for循环套一个二分，那么时间复杂度则为O(nlogn)。本回答被提问者和网友采纳

如何计算以下函数的时间复杂度？

【中文标题】如何计算以下函数的时间复杂度？

【英文标题】：How do I calculate the time complexity of the following function?

【发布时间】：2021-06-10 14:30:09

【问题描述】：

这是一个递归函数。它遍历字符串映射（multimap<string, string> graph）。检查itr -> second (s_tmp) 如果s_tmp 等于所需的字符串(Exp)，打印它(itr -> first) 并再次为itr -> first 执行函数。

string findOriginalExp(string Exp)
    cout<<"*****findOriginalExp Function*****"<<endl;
    string str;
    if(graph.empty())
        str ="map is empty";
    else
        for(auto itr=graph.begin();itr!=graph.end();itr++)
        string s_tmp = itr->second;
        string f_tmp = itr->first;
        string nll = "null";
        //s_tmp.compare(Exp) == 0
        if(s_tmp == Exp)
            if(f_tmp.compare(nll) == 0)
            cout<< Exp <<" :is original experience.";
            return Exp;
            else
                return findOriginalExp(itr->first);

            
        else
            str="No element is equal to Exp.";
        
     

    
    return str;
    

没有停止的规则，它似乎是完全随机的。这个函数的时间复杂度是怎么计算的？

【问题讨论】：

顺便说一句，你能发布一个最小的、可重现的例子吗？

请注意，我只是偶然看到您的评论。仅当该用户有先前的评论时，通过 @ ping 才有效。 UB 已消失，但您可以通过添加 graph 的定义以及它的一些内容示例来改进问题。

如果您不需要分析答案，可以使用google-benchmark 进行实验。

您可能应该正确缩进您的代码。我不确定您是否缺少支架（在移动设备上，因此无法轻松检查）

我想我必须输入所有代码。我只想知道，当一个函数（递归函数）随机结束时，是否可以计算时间复杂度？与这里发生的事情相反（***.com/questions/13467674/…）。也就是说，可以找到一条规则来终止递归函数。

【参考方案1】：

这个函数接受一个有向图和该图中的一个顶点，并向后追踪进入它的边以找到一个没有边指向它的顶点。查找任何给定顶点“后面”的顶点的操作将n 中的O(n) 字符串比较@ 图中的k/v 对数（这是for 循环）。它会这样做m 次，其中m 是它必须遵循的路径的长度（它通过递归实现）。因此，它在n k/v 对的数量和m 路径长度中具有O(m * n) 字符串比较的时间复杂度。

请注意，对于您在代码中看到的某些函数，通常没有“时间复杂度”之类的东西。您必须定义要用来描述时间的变量，以及要用来测量时间的操作。例如。如果我们想纯粹按照n k/v 对的数量来写这个，就会遇到问题，因为如果图形包含适当放置的循环，函数不会终止！ 如果你进一步将图约束为非循环的，那么任何路径的最大长度都受到m < n的约束，然后你还可以得到这个函数对非循环的O(n^2)字符串比较带有n 边的图形。

【参考方案2】：

我不打算分析您的功能，而是尝试以更一般的方式回答。看起来您正在寻找一个简单的表达式，例如 O(n) 或 O(n^2) 来表示您的函数的复杂性。然而，复杂性并不总是那么容易估计。

在您的情况下，这在很大程度上取决于 graph 的内容以及用户作为参数传递的内容。

作为一个类比考虑这个函数：

int foo(int x)
    if (x == 0) return x;
    if (x == 42) return foo(42);        
    if (x > 0) return foo(x-1);            
    return foo(x/2);

在最坏的情况下，它永远不会返回给调用者。如果我们忽略x >= 42，那么最坏情况的复杂度是O(n)。仅此一项作为对用户的信息并没有那么有用。作为用户，我真正需要知道的是：

永远不要用x >= 42 调用它。 O(1) 如果x==0 O(x) 如果x>0 O(ln(x)) 如果x < 0

现在尝试对您的函数进行类似的考虑。最简单的情况是Exp 不在graph 中，在这种情况下没有递归。我几乎可以肯定，对于“正确”的输入，您的函数可以永远不会返回。找出这些案例并记录下来。在这两者之间，您有一些案例在有限数量的步骤后返回。如果您完全不知道如何通过分析掌握它们，您可以随时设置基准和衡量标准。测量输入大小10、50、100、1000.. 的运行时间应该足以区分线性、二次和对数相关性。

PS：只是一个提示：不要忘记代码实际上应该做什么以及解决该问题所需的时间复杂度（通常更容易以抽象的方式讨论，而不是深入研究代码）。在上面这个愚蠢的例子中，整个函数可以替换为等效的int foo(int) return 0; ，它显然具有恒定的复杂性，不需要比这更复杂。

【讨论】：

非常感谢。我明白。我会照你说的做。

nit：渐近复杂度是一个定义明确的术语，在示例中很容易估计（因为当 n 接近无穷大时很明显）。但它并不总是有用的。而且 on 总是可以写一些特别做作的函数，这些函数真的很难分析。

@DanM。你的挑剔是完全合适的。我感觉到了一个轻微的误解，并用一个例子来说明一些事情。充其量这是一半的答案。我的目标不是最佳答案，如果我减少了 OP 获得不那么随意的答案的机会，我很抱歉......

【参考方案3】：

您应该使用递归关系来近似递归调用的控制流程。自从我上离散数学的大学课程以来已经有 30 年了，但通常你确实喜欢伪代码，足以看到有多少调用。在某些情况下，仅计算右侧最长条件的数量是有用的，但您通常需要重新插入一个展开式，并从中推导出多项式或幂关系。

【讨论】：

我想我必须输入所有代码。我只是想知道，是否可以计算函数（递归函数）随机结束时的时间复杂度？与这里发生的事情相反（***.com/questions/13467674/...）。也就是说，可以找到一条规则来终止递归函数。

也许...看看放射性衰变（随机）如何为您提供可预测的半衰期。如果递归以概率终止，您可能会得到一系列收敛的分数。