[题解]洛谷比赛『期末考后的休闲比赛2』
Posted 阿波罗2003
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[题解]洛谷比赛『期末考后的休闲比赛2』相关的知识,希望对你有一定的参考价值。
前言(在题解前面瞎扯的话)
这场比赛已经结束了有几天,但我各种忙,虽然AK但还是没来得及写题解。(我才不会告诉你我跑去学数据结构了)
T1 区间方差
(就不贴题好了)
首先可以推公式(我们可以知道,线段树然而并不能通过初中学过的方差公式在log(L)内求出方差):
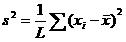
(s2表示方差,L表示区间长度,xi表示区间的每一项,最后一个x上画了一根线表示这些数据的平均数)
用二项式定理完全平方公式可得:
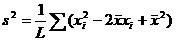
再次展开:
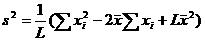
另外,再代入以下这个
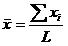
得到了:
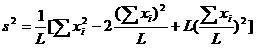
然后继续吧。。
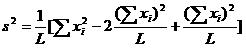
然后duang地一声合并同类项,于是我们得到了:
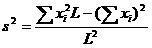
然后可以高兴地发现,和 和 平方和都是线段树的拿手好戏,然而按照这么写估计只能过几个点。
很明显平方和肯定会超long long,难不成还要写一个高精度?
仔细读读题,然后就发现可以模一个1e9+7。然后处处取模(笑),最后就能够水掉这道水题了。
至于求逆元,可以用在线算法,扩展欧几里得、快速幂(好像是基于欧拉定理),也可以用线性推逆元预处理所有可能用到的逆元。
Code(线段树)
1 /** 2 * luogu.org 3 * Problem#2005 4 * Accepted 5 * Time:965ms / 691ms 6 * Memory:18601k / 18601k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<cstdio> 12 #include<cstdlib> 13 #include<cstring> 14 #include<ctime> 15 #include<cctype> 16 #include<cmath> 17 #include<algorithm> 18 #include<stack> 19 #include<queue> 20 #include<set> 21 #include<map> 22 #include<vector> 23 using namespace std; 24 typedef bool boolean; 25 #define smin(a, b) (a) = min((a), (b)) 26 #define smax(a, b) (a) = max((a), (b)) 27 template<typename T> 28 inline void readInteger(T& u){ 29 char x; 30 int aFlag = 1; 31 while(!isdigit((x = getchar())) && x != \'-\' && x != -1); 32 if(x == -1) return; 33 if(x == \'-\'){ 34 x = getchar(); 35 aFlag = -1; 36 } 37 for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - \'0\'); 38 ungetc(x, stdin); 39 u *= aFlag; 40 } 41 42 const int moder = 1000000007; 43 44 template<typename T1, typename T2> 45 class Pair{ 46 public: 47 T1 x; 48 T2 y; 49 Pair(T1 x, T2 y):x(x), y(y){ } 50 Pair operator +(Pair another){ 51 return Pair(x + another.x % moder, y + another.y % moder); 52 } 53 }; 54 55 typedef class TreeNode{ 56 public: 57 int sum; 58 int sum2; 59 int from, end; 60 TreeNode* left, *right; 61 TreeNode(long long sum, int from, int end):from(from), end(end), left(NULL), right(NULL), sum(sum){ 62 sum2 = sum * sum % moder; 63 } 64 void pushUp(){ 65 this->sum = this->left->sum + this->right->sum; 66 this->sum %= moder; 67 this->sum2 = this->left->sum2 + this->right->sum2; 68 this->sum2 %= moder; 69 } 70 }TreeNode; 71 72 typedef class SegTree{ 73 public: 74 TreeNode* root; 75 76 SegTree():root(NULL){ } 77 SegTree(int size, int* val){ 78 build(root, 1, size, val); 79 } 80 81 void build(TreeNode*& node, int from, int end, int* val){ 82 node = new TreeNode(0, from, end); 83 if(from == end){ 84 node->sum = val[from]; 85 node->sum2 = (int)(val[from] * 1LL * val[from] % moder); 86 return; 87 } 88 int mid = (from + end) >> 1; 89 build(node->left, from, mid, val); 90 build(node->right, mid + 1, end, val); 91 node->pushUp(); 92 } 93 94 void update(TreeNode*& node, int index, int val){ 95 if(node->from == index && node->end == index){ 96 node->sum = val; 97 node->sum2 = (int)(val * 1LL * val % moder); 98 return; 99 } 100 int mid = (node->from + node->end) >> 1; 101 if(index <= mid) update(node->left, index, val); 102 else update(node->right, index, val); 103 node->pushUp(); 104 } 105 106 Pair<long long, long long> query(TreeNode*& node, int from, int end){ 107 if(node->from == from && node->end == end){ 108 return Pair<long long, long long>(node->sum, node->sum2); 109 } 110 int mid = (node->from + node->end) >> 1; 111 if(end <= mid) return query(node->left, from, end); 112 if(from > mid) return query(node->right, from, end); 113 return query(node->left, from, mid) + query(node->right, mid + 1, end); 114 } 115 116 }SegTree; 117 118 /* 119 int pow_mod(int x, int pos){ 120 if(pos == 1) return x; 121 int temp = pow_mod(x, pos / 2); 122 if(pos & 1) return (int)(temp * 1LL * temp % moder * x % moder); 123 return (int)(temp * 1LL * temp % moder); 124 } 125 */ 126 127 void gcd(int a, int b, int& d, int& x, int& y){ 128 if(b == 0){ 129 d = a;x = 1;y= 0; 130 }else{ gcd(b, a % b, d, y, x); y -= x * (a / b); } 131 } 132 133 int getInv(int a, int n){ 134 int d, x, y; 135 gcd(a, n, d, x, y); 136 return (x + n) % n; 137 } 138 139 int n, m; 140 SegTree st; 141 int* initer; 142 143 inline void init(){ 144 readInteger(n); 145 readInteger(m); 146 initer = new int[(const int)(n + 1)]; 147 for(int i = 1; i <= n; i++) 148 readInteger(initer[i]); 149 st = SegTree(n, initer); 150 } 151 152 inline void solve(){ 153 int op, a, b; 154 while(m--){ 155 readInteger(op); 156 readInteger(a); 157 readInteger(b); 158 if(op == 1){ 159 st.update(st.root, a, b); 160 }else if(op == 2){ 161 Pair<long long, long long> p = st.query(st.root, a, b); 162 long long L = b - a + 1; 163 // long long inv = pow_mod(L * L % moder, moder - 2); 164 int inv = getInv(L * L % moder, moder); 165 long long fm = (L * (p.y % moder) % moder - p.x * p.x % moder + moder) % moder; 166 long long ans = fm * inv % moder; 167 printf("%d\\n", (int)ans); 168 } 169 } 170 } 171 172 int main(){ 173 init(); 174 solve(); 175 return 0; 176 }
不过这道题只有单点修改,那么,可以考虑用树状数组。树状数组的常数比线段树小这是家喻户晓的事情(两者理论时间复杂度一样)。
另外鉴于洛谷鬼蓄的评测机,把某些只超一点点的取模符号改成三目运算符,就快了100多ms(吐血)。
由于我比较懒,又赶去学Splay,所以没有来得急写。
T2 漂浮的鸭子
一道强连通分量的裸题。常见的算法是Tarjan:
1 /** 2 * luogu.org 3 * Problem#2049 4 * Accepted 5 * Time:150ms 6 * Memory:18527k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<cstdio> 12 #include<cstdlib> 13 #include<cstring> 14 #include<ctime> 15 #include<cctype> 16 #include<cmath> 17 #include<algorithm> 18 #include<stack> 19 #include<queue> 20 #include<set> 21 #include<map> 22 #include<vector> 23 using namespace std; 24 typedef bool boolean; 25 #define smin(a, b) (a) = min((a), (b)) 26 #define smax(a, b) (a) = max((a), (b)) 27 template<typename T> 28 inline void readInteger(T& u){ 29 char x; 30 int aFlag = 1; 31 while(!isdigit((x = getchar())) && x != \'-\' && x != -1); 32 if(x == -1) return; 33 if(x == \'-\'){ 34 x = getchar(); 35 aFlag = -1; 36 } 37 for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - \'0\'); 38 ungetc(x, stdin); 39 u *= aFlag; 40 } 41 42 int cv = 0, cc = 0; 43 stack<int> s; 44 int* visitID; 45 int* exitID; 46 boolean* instack; 47 boolean* visited; 48 int* belong; 49 int* next; 50 51 void getSonMap(int end){ 52 int d; 53 cc++; 54 do{ 55 d = s.top(); 56 s.pop(); 57 belong[d] = cc; 58 instack[d] = false; 59 }while(d != end); 60 } 61 62 void Tarjan(int node){ 63 visitID[node] = exitID[node] = ++cv; 64 visited[node] = true; 65 s.push(node); 66 instack[node] = true; 67 if(!visited[next[node]]){ 68 Tarjan(next[node]); 69 smin(exitID[node], exitID[next[node]]); 70 }else if(instack[next[node]]){ 71 smin(exitID[node], visitID[next[node]]); 72 } 73 if(exitID[node] == visitID[node]) 74 getSonMap(node); 75 } 76 77 int n; 78 int *len; 79 int *clen; 80 81 inline void init(){ 82 readInteger(n); 83 visitID = new int[(const int)(n + 1)]; 84 exitID = new int[(const int)(n + 1)]; 85 instack = new boolean[(const int)(n + 1)]; 86 visited = new boolean[(const int)(n + 1)]; 87 belong = new int[(const int)(n + 1)]; 88 next = new int[(const int)(n + 1)]; 89 len = new int[(const int)(n + 1)]; 90 memset(visited, false, sizeof(boolean) * (n + 1)); 91 memset(instack, false, sizeof(boolean) * (n + 1)); 92 for(int i = 1; i <= n; i++){ 93 readInteger(next[i]); 94 readInteger(len[i]); 95 } 96 } 97 98 int result = 0; 99 boolean* vis; 100 101 inline void solve(){ 102 for(int i = 1; i <= n; i++) 103 if(!visited[i]) 104 Tarjan(i); 105 delete[] visitID; 106 delete[] visited; 107 delete[] instack; 108 delete[] exitID; 109 clen = new int[(const int)(cc + 1)]; 110 vis = new boolean[(const int)(cc + 1)]; 111 memset(vis, false, sizeof(boolean) * (cc + 1)); 112 for(int i = 1; i <= n; i++){ 113 if(!vis[belong[i]]){ 114 int j = i; 115 int l = 0; 116 while(belong[next[j]] == belong[i] && next[j] != i){ 117 l += len[j]; 118 j = next[j]; 119 } 120 l += len[j]; 121 vis[belong[i]] = true; 122 smax(result, l); 123 } 124 } 125 printf("%d", result); 126 } 127 128 int main(){ 129 init(); 130 solve(); 131 return 0; 132 }
仔细读题,每个点的出度为1,那么实际上dfs就好了,用不着Tarjan,还开辣么多数组。
1 /** 2 * luogu.org 3 * Problem#2049 4 * Accepted 5 * Time:107ms 6 * Memory:17941k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<cstdio> 12 #include<cstdlib> 13 #include<cstring> 14 #include<ctime> 15 #include<cctype> 16 #include<cmath> 17 #include<algorithm> 18 #include<stack> 19 #include<queue> 20 #include<set> 21 #include<map> 22 #include<vector> 23 using namespace std; 24 typedef bool boolean; 25 #define smin(a, b) (a) = min((a), (b)) 26 #define smax(a, b) (a) = max((a), (b)) 27 template<typename T> 28 inline void readInteger(T& u){ 29 char x; 30 int aFlag = 1; 31 while(!isdigit((x = getchar())) && x != \'-\' && x != -1); 32 if(x == -1) return; 33 if(x == \'-\'){ 34 x = getchar(); 35 aFlag = -1; 36 } 37 for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - \'0\'); 38 ungetc(x, stdin); 39 u *= aFlag; 40 } 41 42 int n; 43 int cc = 0; 44 int *belong; 45 int *next; 46 int *len; 47 int *dist; 48 int result = 0; 49 50 void dfs(int node, int be){ 51 belong[node] = be; 52 if(belong[next[node]] == be){ 53 int dis = dist[node] - dist[next[node]] + len[node]; 54 smax(result, dis); 55 } 56 if(belong[next[node]] == 0){ 57 dist[next[node]] = dist[node] + len[node]; 58 dfs(next[node], be); 59 } 60 } 61 62 inline void init(){ 63 readInteger(n); 64 belong = new int[(const int)(n + 1)]; 65 next = new int[(const int)(n + 1)]; 66 len = new int[(const int)(n + 1)]; 67 dist = new int[(const int)(n + 1)]; 68 memset(belong, 0, sizeof(int) * (n + 1)); 69 for(int i = 1; i <= n; i++){ 70 readInteger(next[i]); 71 readInteger(len[i]); 洛谷题解part[NOIP2015提高&洛谷P2678]跳石头 题解(二分答案)