AOV网

Posted 2020-08-21 KennyRom

1、定义

用顶点表示活动，用有向边<Vi, Vj>表示活动间的优先关系。

Vi必须先于活动Vj进行。

这种有向图叫做顶点表示活动的AOV网络（Activity On Vertices）

 

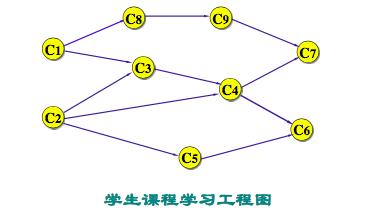
2、拓扑排序

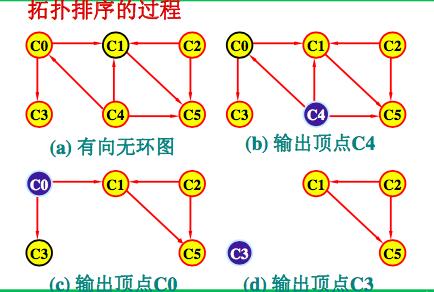
拓扑序列：即将各个顶点（代表各个活动）排列成一个线性有序的序列，使得所有弧尾结点排在弧头结点的前面。

 

这种构造AOV网络全部顶点的拓扑有序序列的运算叫做拓扑排序。

 

如果通过拓扑排序能将AOV网络的所有顶点都排入一个拓扑有序的序列中，则一定没有有向环。

 

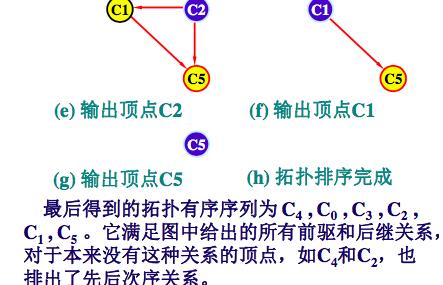
上图的拓扑排序为：

C1，C8，C2，C3，C5，C9，C4，C7，C6

 

拓扑排序方法：

（1）输入AOV网络。令n为顶点个数；

（2）在AOV网络中选一个没有直接前驱的顶点，并输出之；

（3）从图中删去该顶点，同时删去所有它发出的有向边；

（4）重复以上（2）（3）步，直到

         全部顶点均已输出，拓扑有序序列形成，拓扑排序完成；

   或

         图中还有未输出的顶点，但已跳出处理循环。说明图中还剩下一些顶点，它们都有直接前驱，这是网络中必有环。

 

 

如果图采用邻接表储存，则在邻接表中增设一个数组count[]，记录各顶点入度。入度为0的顶点即无前驱顶点。

在输入数据前，顶点表data[]和入度数组count[]全部初始化。

在输入数据时，每输入一条边<j, k >,就需要建立一个边结点，并将它链入相应边链表中，统计入度信息：

EdgeNode *p = new EdgeNode;
p->adjvex = k;
p->nextarc = G.VexList[j].firstarc;
data[j].firstarc = p;
count[k]++;

　　

 

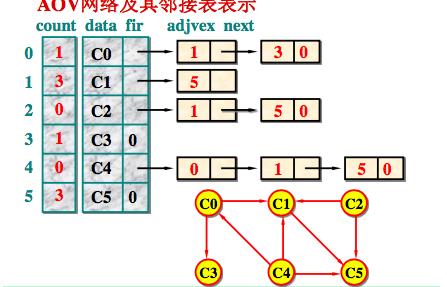
在算法中，使用一个存放入度为0的顶点的链式栈，供选择和输出无前驱的顶点。

 

算法描述：

建立入度为0的顶点栈；

当入度为0的顶点栈不为空时，重复执行

    从顶点栈中推出一个顶点，并输出之；

    从AOV网络中删去这个顶点和它发出的边，边的总顶点入度减一；

    如果边的终顶点入度减至0，则该顶点进入入度为0的顶点栈；

如果输出顶点个数少于AOV网络的顶点个数，则报告网络中存在有向环。

 

算法分析：

如果AOV网络中有n个顶点，e条边，在拓扑排序的过程中，搜索入度为0的顶点，建立链式栈所需要的时间是O(n)。在正常的情况下，有向图有n个顶点，每个顶点进入一次栈，出一次栈，共输出n次。顶点入度减一的运算共执行了e次。所以总的时间复杂度为O(n+e).