AOV网上的拓扑排序|拓扑序列所有拓扑序列的求解

Posted 2021-07-14 没头发的米糊

在本篇博客中，将介绍AOV网上的拓扑排序，以及如何实现输出所有拓扑序列。

目录

前置概念

AOV(Activity on Vertex)网

在一个表示工程的有向图中，用顶点表示活动，用有向弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，简称AOV(Activity on Vertex)网。

弧表示工程活动之间的某种前后制约关系，AOV网中不能存在回路，即不能存在环，否则某个活动的开始要以自己完成作为先决条件，这是不现实的。

如下是一个AOV网的例子。

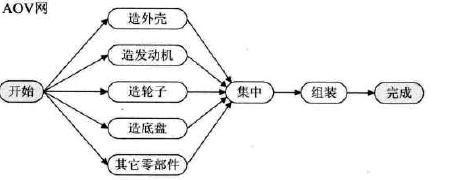
AOE(Activity on Edge)网

在一个表示工程的带权有向图中，用顶点表示状态，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，简称AOE(Activity on Edge)网。

始点/源点：有向图中没有入边的顶点，表示一个工程的开始

终点/汇点：有向图中没有出边的顶点，表示一个工程的结束

某个顶点代表的状态出现后，从该顶点出发的各活动可以立马开始。只有在进入某顶点的各活动都已经结束，该顶点代表的状态才会发生。

如下是一个AOE网的例子。

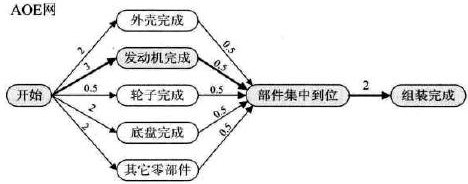
拓扑序列

设G=（V，E）是一个具有n个顶点的有向图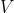，中的顶点序列~，满足若从顶点到有一条路径，则在顶点序列中顶点必定在之前，则我们称这样的顶点序列为一个拓扑序列。

简单来说，在AOV和AOE网上的拓扑序列就是工程活动进行或状态发生上必须遵循的先后关系，显然，一个工程中，拓扑序列可能是不唯一的。

如下是为上述AOV网中的活动编号后，结点的部分拓扑序列。

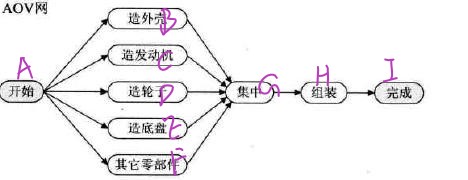
ABCDEFGHI	ABCDFEGHI
ABCEDFGHI	ABCEFDGHI
ABCFEDGHI	............

求解AOV网上的拓扑序列

基本思想

（1）从AOV网中选择一个没有前驱的结点并输出。

（2）从AOV网中删去该结点，并且删去该结点连接的弧。 

（3）重复上述操作，直至所有结点全部被输出，或AOV网中不再存在没有前驱的结点。

具体思路

数据结构

我们使用邻接表来存储图结构，在存储AOV网时，为了方便地得知每个结点是否存在前驱，在顶点表中添加一个入度域。

同时，准备一个栈S，用于存储所有无前驱的顶点。

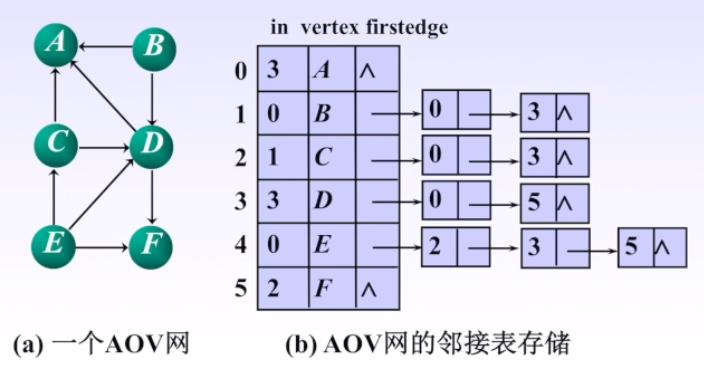
上图是一个AOV网和它的邻接表存储的示意图。

过程思路

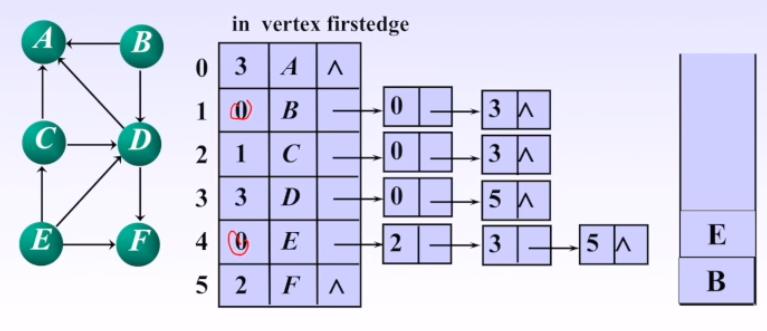
1.在排序开始前，先将所有入度为0的顶点入栈。

2.反复出栈，即删去入度为0的顶点。出栈时需要将要删除的顶点指向的顶点的入度减1，同时把入度变为0的顶点入栈。如此反复，以模拟删除入度为0的顶点和与其连接的边的操作。

代码实现

void AovNetwork::topSort()
{
    cout << "topSort: ";
    //首先将入度为0的顶点入栈。
    for(int i = 0 ; i < length ; i ++)
    {
        if(vertexList[i].inDegree == 0) vexStack.push_back(vertexList + i);
    }
    //反复删除栈顶元素对应的顶点，直至不再存在入度为0的顶点。
    while(!vexStack.empty())
    {
        VertexNode *tempVex = vexStack.back();
        vexStack.pop_back();
        cout << tempVex -> name << " ";
        EdgeNode *tempEdge = tempVex -> firstEdge;
        while(tempEdge != nullptr)
        {
            vertexList[tempEdge->adjVex].inDegree --;
            //同时也需要将入度变为0的顶点入栈。
            if(vertexList[tempEdge->adjVex].inDegree == 0)
            {
                vexStack.push_back(vertexList + tempEdge -> adjVex);
            }
            tempEdge = tempEdge -> next;
        }
    }
    // Restore the network.
    for(int i = 0 ; i < length ; i ++)
    {
        EdgeNode *tempEdge = vertexList[i].firstEdge;
        while(tempEdge != nullptr)
        {
            vertexList[tempEdge -> adjVex].inDegree ++;
            tempEdge = tempEdge -> next;
        }
    }
    cout << endl;
}

所有拓扑序列的求解

基本思路

在如上的实现下，仅能输出一个拓扑排序序列，原因在于每次删除结点时只选择删除栈顶的结点，实际上在删除结点时存在分支，即可以选择删除其他结点，从而走不同的拓扑路径。

因此将栈改为vector，在每次删除结点时应遍历整个vector，走不同的分支，利用递归来实现，在递归进入下一个分支之后，还需要将邻接表的相关关系恢复到进入递归函数前的状态，即回溯的思想。

伪代码如下：

topSort_ALL(string 拓扑路径)

{

        for each vector中的结点（当前入度为0的结点）

        {

                删除该结点，

                同时删除AOV网中与该节点连接的边，

                并将新的入度为0的结点加入vector中。

                

                topSort_ALL(string 拓扑路径+当前结点)

        

                恢复被删除的结点，

                同时恢复AOV网中与该节点连接的边，

                并且删除vector中被添加的入度为0的结点。

        }

}

代码实现 

void AovNetwork::topSort_ALL()
{
    cout << "topSort_ALL: " << endl;
    for(int i = 0 ; i < length ; i ++)
    {
        if(vertexList[i].inDegree == 0) vexStack.push_back(vertexList + i);
    }
    string tempStr;
    dfs_topSort_ALL(tempStr);
}

void AovNetwork::dfs_topSort_ALL(string &tempStr)
{
    if(vexStack.empty())
    {
        cout << tempStr << endl;
    }
    else
    {
        for(int i = 0 ; i < vexStack.size() ; i ++)
        {
            VertexNode *tempVex = vexStack[i];
            vexStack.erase(vexStack.begin() + i);
            tempStr += tempVex -> name;
            tempStr += " ";
            EdgeNode *tempEdge = tempVex -> firstEdge;
            while(tempEdge != nullptr)
            {
                vertexList[tempEdge->adjVex].inDegree --;
                if(vertexList[tempEdge->adjVex].inDegree == 0)
                {
                    vexStack.push_back(vertexList + tempEdge -> adjVex);
                }
                tempEdge = tempEdge -> next;
            }

            dfs_topSort_ALL(tempStr);

            //Backtracking.
            tempEdge = tempVex -> firstEdge;
            while(tempEdge != nullptr)
            {
                if(vertexList[tempEdge->adjVex].inDegree == 0)
                {
                    vexStack.pop_back();
                }
                vertexList[tempEdge->adjVex].inDegree ++;
                tempEdge = tempEdge -> next;
            }
            tempStr.pop_back();
            tempStr.pop_back();
            vexStack.insert(vexStack.begin() + i,tempVex);
        }
    }
}

总结

拓扑排序是基础的数据结构算法，需要多加练习。

同时要注意递归的回溯思想，熟练地使用递归+回溯+记忆化这一套模板式的武功。