图论算法之图形变化原理aov网与拓扑排序

Posted 2021-09-08 踩踩踩从踩

前言

平时在动画或者图像显示中，使用的matrix去表示，而该表示来源于数学中的矩阵。而图论中aov网，以及拓扑排序都是现实中比较常用的，因此本篇文章主要是为了描述出什么是图形变化以及aov网与拓扑排序这些思想。

图形变化原理

常在android开发中有个matrix的概念用来绘制图画及图像，因此学习图形变换首先需要了解什么是矩阵，矩阵的加减乘除

矩阵规则

• 用下面两个矩阵相乘，也就是 3行2列乘以2行3列， 注意如果是3行两列，另外一个矩阵一定要是2行 才能相乘

*  

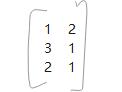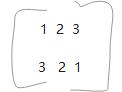
•  先1*2 +2*3     1*2+2*2  1*3+2*1

•  不断就得到矩阵相乘

 

 图像变换

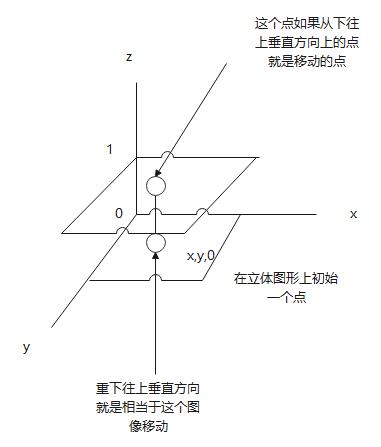
 从下往上垂直照射点为另一个平面上的点，就相当于图像移动

而把照射光源进行放大就是会把这个点扩大

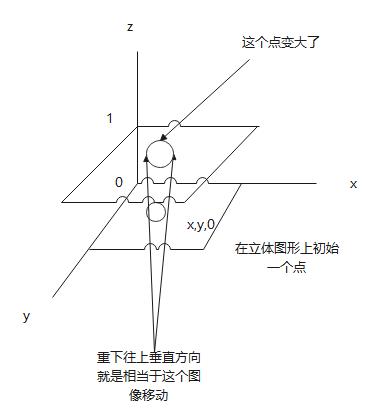
 然后我们在取一个矩阵作为作为光源 往上扩展，是这个点平移另外一个平面，投影出来下面的结果

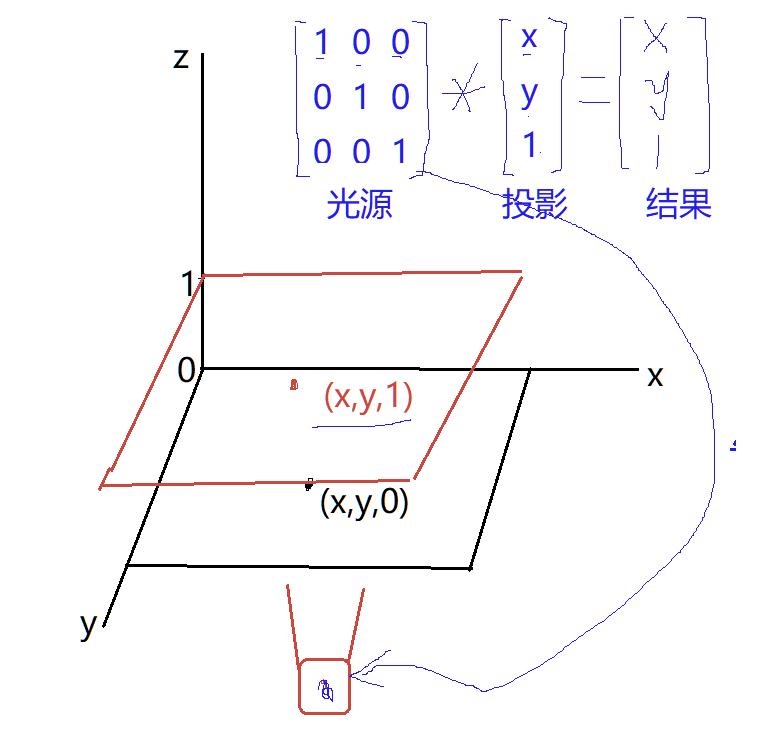
    进行投影产生结果

• 图形间变换然后将矩阵进行调整，改变成下面的矩阵

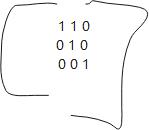
 那么得到的结果就是，下面的变形

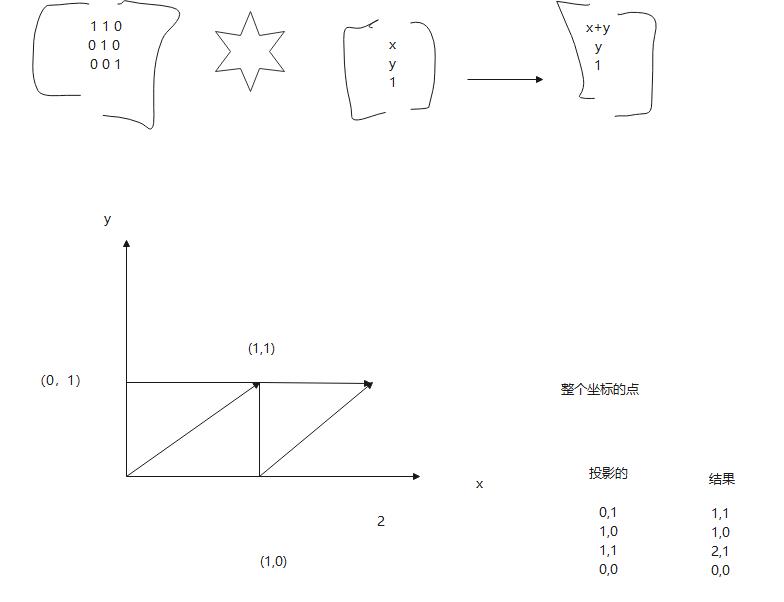
 最后变成横向拉伸图形

• 如果将矩阵进行下面变换，我们又会将下面图形进行变换

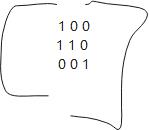
 然后得到下面的结果，沿y轴进行拉伸

 

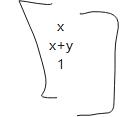
 这就是图形变换中的拉伸，按照矩阵按x和y进行变换就得到了拉伸的效果

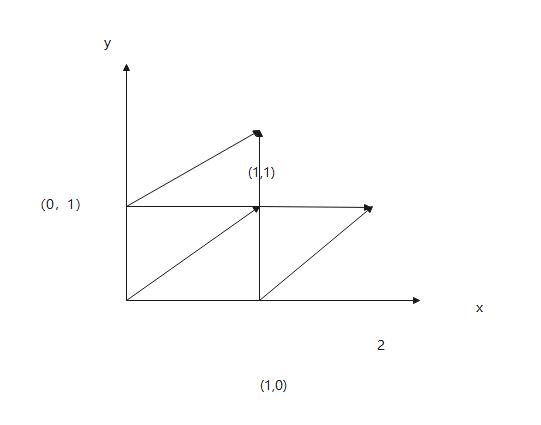
然后继续深入看一下矩阵缩放

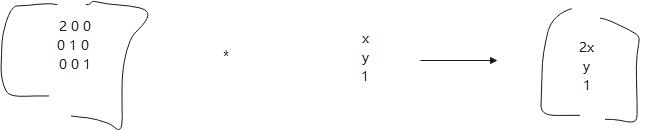
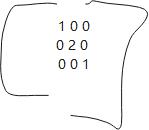
 将1变成2时，所得到的矩阵就变成上面的，在坐标轴上展示出来

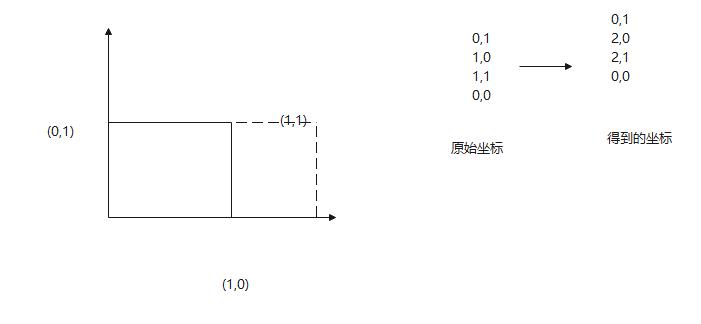
 由上图进行变换的坐标轴， 由原始的坐标，进行变换到得到的坐标，下一部分，这样是不是横向的放大了一倍，

然后如果将中间变成了2，则得到的图形就行从y轴进行变大了一倍。

这就是平时怎么对图像进行变大的

图形平移

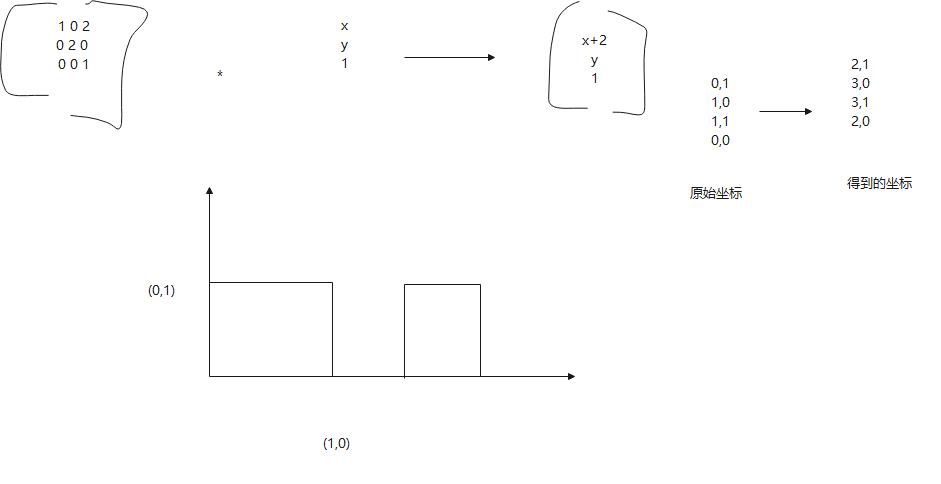
 道理是一样的，就是坐标轴 ， 上变化，光线投影 进行图形的变化

旋转

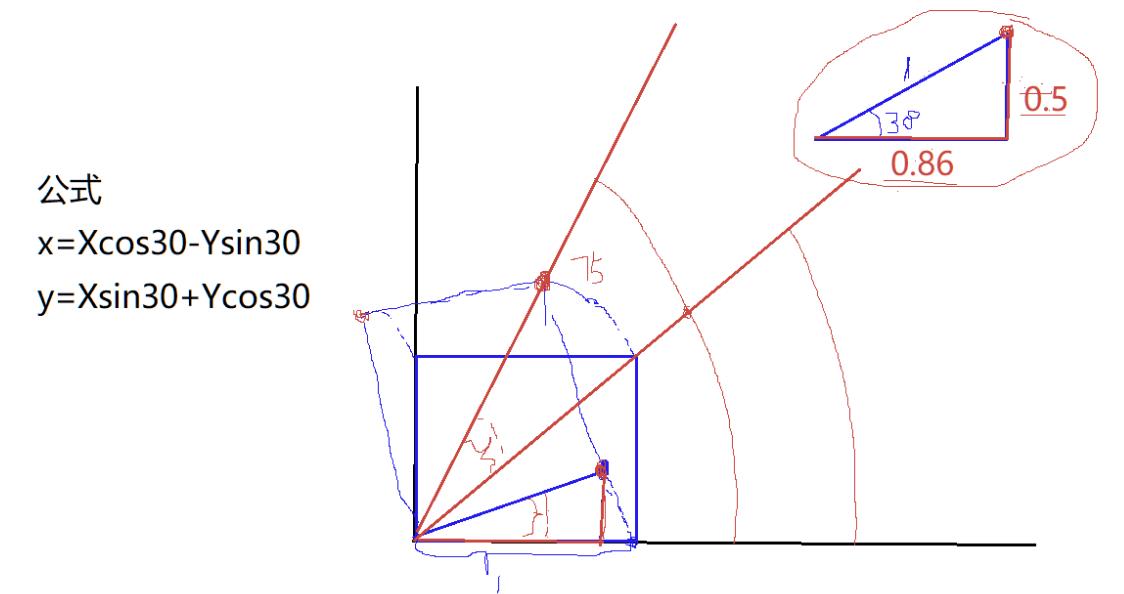
这里需要用到下面的公式

公式
x=Xcos30-Ysin30
y=Xsin30+Ycos30

单位距阵
cos  -sin  0
sin   cos  0
0      0      1

这样 通过点位进行运算得到

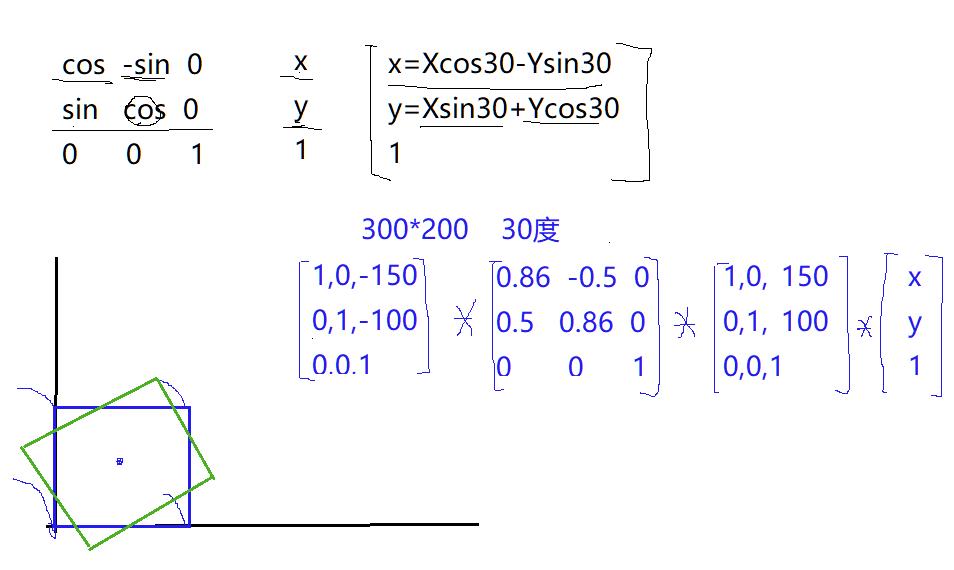
 主要是利用公式进行计算的到图像旋转原理，这就是整个图像进行变换的原理。

AOV网与拓扑排序

AOE网主要用在如何计算一个工程的完工时间和优化工程方案减少工程完工时间；

对最优路径进行选择，选择最优方案

而aov网则是aoe网的简化版，它只考虑先后路径，不考虑最优的路径，

概念：

人们常用有向图来描述和分析一项工程的计划和实施过程，一个工程通常被分为多个小工程，这些子工程被称为活动(activity) ，在有向图中若以顶点表示活动，有向边表示活动的先后关系，这样的图简称为aov网

要做某件事，必须要做某件事，aov网有向无环的图

任何具有先后顺序的都可以用aov网进行表示

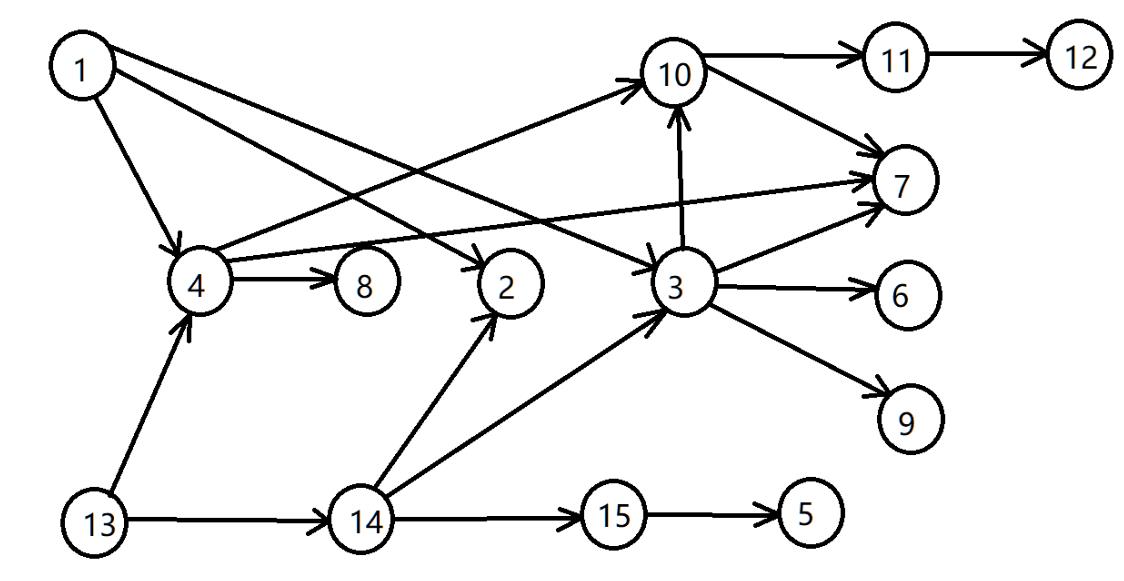
 例如 1，13，4，8，14，15，5，2，3，10，6，9，11，12，7

某一种顺序 得到序列就被称为拓扑序列，这种序列是不能回退的； 

图论辅助决策性工作

 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

产生拓扑序列的算法

• 从AOV网中选择一个没有前趋的顶点（即入度为零),并输出它
• 从网中删除该顶点，并且删除从该顶点发出的全部有向边
• 重复1和2

用邻接表而不用邻接矩阵表示

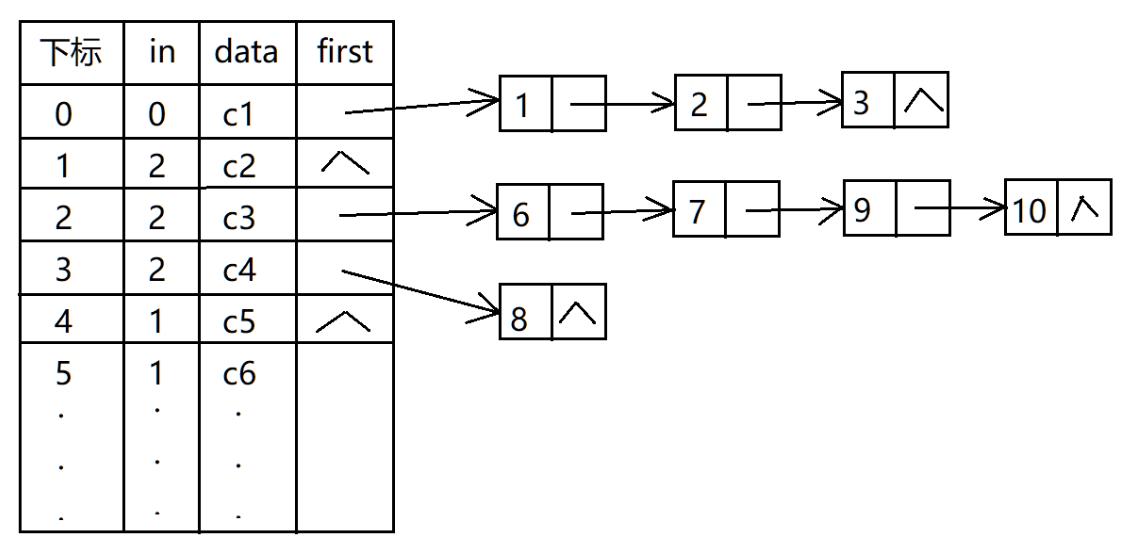
 其中in表示 入度  first表示出度，data 表示当前数据    指向下标 这种表示方式，在图论基础篇讲到的，具体的不详解

代码实现

• 新建一个邻接表

 /**
     * 边表结点
     */
    class EdgeNode{
        int data;
        EdgeNode next;

        public EdgeNode(int data, EdgeNode next) {
            this.data = data;
            this.next = next;
        }
    }
    /**
     * 顶点表结点
     */
    class VertexNode{
        int in;//入度
        int data;
        EdgeNode first;

        public VertexNode(int in, int data, EdgeNode first) {
            this.in = in;
            this.data = data;
            this.first = first;
        }
    }

用边表和顶点表来分开，进行实现，每一行表示，入度为多少，和出度

• 造一份邻接图表

  EdgeNode a=new EdgeNode(3,null);
        EdgeNode a2=new EdgeNode(2,a);
        EdgeNode a3=new EdgeNode(1,a2);
        graphAdjList[0]=new VertexNode(0,1,a3);
        graphAdjList[1]=new VertexNode(2,2,null);
        EdgeNode b1=new EdgeNode(9,null);
        EdgeNode b2=new EdgeNode(8,b1);
        EdgeNode b3=new EdgeNode(6,b2);
        EdgeNode b4=new EdgeNode(5,b3);
        graphAdjList[2]=new VertexNode(2,3,b4);
        EdgeNode c1=new EdgeNode(7,null);
        EdgeNode c2=new EdgeNode(9,c1);
        EdgeNode c3=new EdgeNode(6,c2);
        graphAdjList[3]=new VertexNode(2,4,c3);
        graphAdjList[4]=new VertexNode(1,5,null);
        graphAdjList[5]=new VertexNode(1,6,null);
        graphAdjList[6]=new VertexNode(3,7,null);
        graphAdjList[7]=new VertexNode(1,8,null);
        graphAdjList[8]=new VertexNode(1,9,null);
        EdgeNode d1=new EdgeNode(10,null);
        EdgeNode d2=new EdgeNode(6,d1);
        graphAdjList[9]=new VertexNode(2,10,d2);
        EdgeNode e1=new EdgeNode(11,null);
        graphAdjList[10]=new VertexNode(1,11,e1);
        graphAdjList[11]=new VertexNode(1,12,null);
        EdgeNode f1=new EdgeNode(3,null);
        EdgeNode f2=new EdgeNode(13,f1);
        graphAdjList[12]=new VertexNode(0,13,f2);
        EdgeNode g1=new EdgeNode(14,null);
        EdgeNode g2=new EdgeNode(1,g1);
        EdgeNode g3=new EdgeNode(2,g2);
        graphAdjList[13]=new VertexNode(1,14,g3);
        EdgeNode h1=new EdgeNode(4,null);
        graphAdjList[14]=new VertexNode(1,15,h1);

这去造一份节点还是比较麻烦的，数组0号位置入度为0，

• 需要一个集合或者栈来存储数据

 

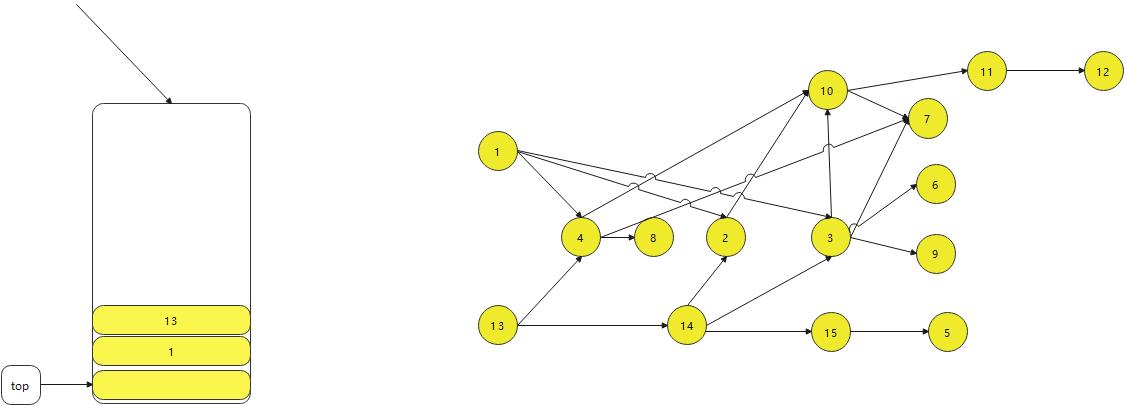
进行不断拿出数据放到集合或者栈中先放1或者13放进去

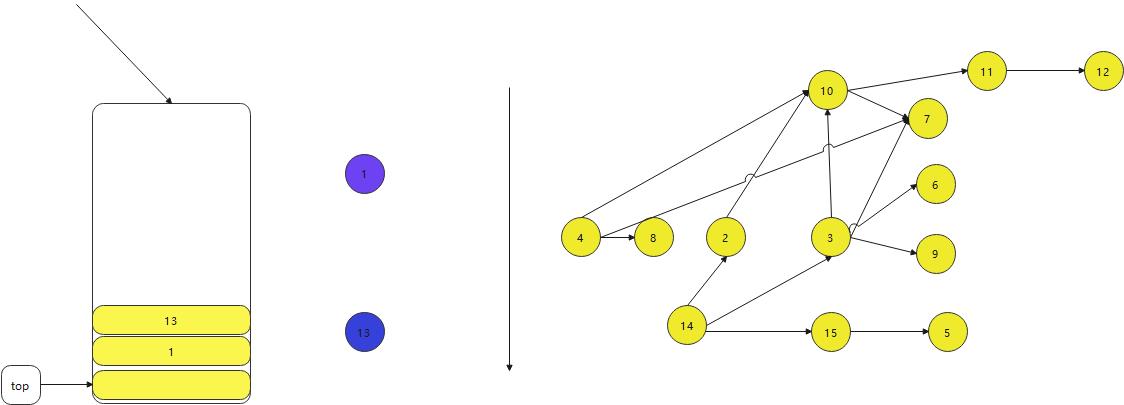
• 这样不断的向下进行放进去，方向这个可以根据算法去选择具体的实现

int top=0;//栈顶指针
        int[] stack=new int[15];//用来存放入度为0的顶点
        //循环得到入度为0的所有顶点
        for (int i = 0; i < graphAdjList.length; i++) {
            if(graphAdjList[i].in==0){
                stack[++top]=i;
            }
        }

遍历得到所有的入度为0的顶点

• 然后判断top指针不等于0则继续拿数据

while(top!=0){
            int getTop=stack[top--];//出栈一个
            System.out.print("  "+graphAdjList[getTop].data);
            //更新当前输出节点所有的出边（后继顶点）
            for(EdgeNode e=graphAdjList[getTop].first;e!=null;e=e.next){
                int k=e.data;
                //入度减一
                graphAdjList[k].in--;
                if(graphAdjList[k].in==0){
                    stack[++top]=k;
                }
            }

        }

 通过不断的遍历拿到数据

总结

本篇文章主要讲解的图的应用算法，包括图像变换原理，主要用通过矩阵间的变换进行图像的拉伸 横移扩大，旋转等操作，这在前端 android等领域应用相当广泛，还包括拓扑排序外部排序算法，aov网，图算法的应用，用于实际生活中。