机器学习——支持向量机(SVM)之核函数(kernel)
Posted tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习——支持向量机(SVM)之核函数(kernel)相关的知识,希望对你有一定的参考价值。
对于线性不可分的数据集,可以利用核函数(kernel)将数据转换成易于分类器理解的形式。
如下图,如果在x轴和y轴构成的坐标系中插入直线进行分类的话, 不能得到理想的结果,或许我们可以对圆中的数据进行某种形式的转换,从而得到某些新的变量来表示数据。在这种表示情况下,我们就更容易得到大于0或者小于0的测试结果。在这个例子中,我们将数据从一个特征空间转换到另一个特征空间,在新的空间下,我们可以很容易利用已有的工具对数据进行处理,将这个过程称之为从一个特征空间到另一个特征空间的映射。在通常情况下,这种映射会将低维特征空间映射到高维空间。
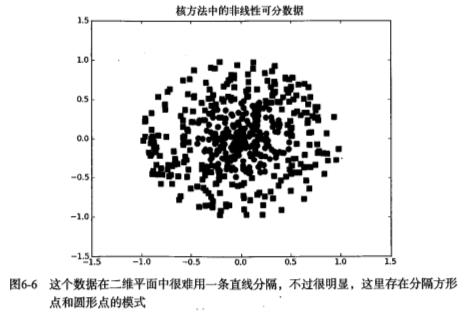
这种从某个特征空间到另一个特征空间的映射是通过核函数来。
SVM优化中一个特别好的地方就是,所有的运算都可以写成内积(inner product)的形式。向量的内积指的就是两个向量相乘,之后得到单个标量或者数值。我们可以把内积运算替换成核函数,而并不必做简化处理。将内积替换成核函数的方法被称之为核技巧(kernel trick)或者核“变电”(kernel substation)。
径向基核函数
径向基核函数是SVM中常用的一个核函数。径向基函数是一个采用向量作为自变量的函数,能够基于向量距离运算输出一个标量。
\'\'\'#######********************************
以下是有核函数的版本
\'\'\'#######********************************
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k): #计算误差
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei): #用于选择第2个循环(内循环)的alpha值,内循环中的启发式方法
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #跳过本身
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE): #选取具有最大步长的j
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don\'t have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k): #alpha改变后,更新缓存
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
#内部循环的代码和简版的SMO代码很相似
def innerL(i, oS):
Ei = calcEk(oS, i)
#判断每一个alpha是否被优化过,如果误差很大,就对该alpha值进行优化,toler是容错率
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #使用启发式方法选取第2个alpha,选取使得误差最大的alpha
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
#保证alpha在0与C之间
if (oS.labelMat[i] != oS.labelMat[j]): #当y1和y2异号,计算alpha的取值范围
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else: #当y1和y2同号,计算alpha的取值范围
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print "L==H"; return 0
#eta是alpha[j]的最优修改量,eta=K11+K22-2*K12,也是f(x)的二阶导数,K表示核函数
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
#如果二阶导数-eta <= 0,说明一阶导数没有最小值,就不做任何改变,本次循环结束直接运行下一次for循环
if eta >= 0: print "eta>=0"; return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta #利用公式更新alpha[j],alpha2new=alpha2-yj(Ei-Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) #判断alpha的范围是否在0和C之间
updateEk(oS, j) #在alpha改变的时候更新Ecache
print "j=",j
print oS.alphas.A[j]
#如果alphas[j]没有调整,就忽略下面语句,本次循环结束直接运行下一次for循环
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #在alpha改变的时候更新Ecache
print "i=",i
print oS.alphas.A[i]
#已经计算出了alpha,接下来根据模型的公式计算b
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
#根据公式确定偏移量b,理论上可选取任意支持向量来求解,但是现实任务中通常使用所有支持向量求解的平均值,这样更加鲁棒
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1 #如果有任意一对alpha发生改变,返回1
else: return 0
#完整版Platt SMO的外循环
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=(\'lin\', 0)):
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): #有alpha改变同时遍历次数小于最大次数,或者需要遍历整个集合
alphaPairsChanged = 0
#首先进行完整遍历,过程和简化版的SMO一样
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS) #i是第1个alpha的下标
print "完整遍历, 迭代次数: %d i:%d, 成对改变的次数 %d" % (iter,i,alphaPairsChanged)
iter += 1
#非边界遍历,挑选其中alpha值在0和C之间非边界alpha进行优化
else:
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] #然后挑选其中值在0和C之间的非边界alpha进行遍历
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print "非边界, 迭代次数: %d i:%d, 成对改变的次数 %d" % (iter,i,alphaPairsChanged)
iter += 1
#如果这次是完整遍历的话,下次不用进行完整遍历
if entireSet: entireSet = False #终止完整循环
elif (alphaPairsChanged == 0): entireSet = True #如果alpha的改变数量为0的话,再次遍历所有的集合一次
print "iteration number: %d" % iter
return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels): #计算模型的参数w,即alpha*y*x转置的累加
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet(\'testSetRBF.txt\')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, (\'rbf\', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelMat[svInd];
print "there are %d Support Vectors" % shape(sVs)[0]
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],(\'rbf\', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the training error rate is: %f" % (float(errorCount)/m)
dataArr,labelArr = loadDataSet(\'testSetRBF2.txt\')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],(\'rbf\', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the test error rate is: %f" % (float(errorCount)/m)
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName) #load the training set
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split(\'.\')[0] #take off .txt
classNumStr = int(fileStr.split(\'_\')[0])
if classNumStr == 9: hwLabels.append(-1)
else: hwLabels.append(1)
trainingMat[i,:] = img2vector(\'%s/%s\' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=(\'rbf\', 10)):
dataArr,labelArr = loadImages(\'trainingDigits\')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
print "there are %d Support Vectors" % shape(sVs)[0]
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the training error rate is: %f" % (float(errorCount)/m)
dataArr,labelArr = loadImages(\'testDigits\')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the test error rate is: %f" % (float(errorCount)/m)
以上是关于机器学习——支持向量机(SVM)之核函数(kernel)的主要内容,如果未能解决你的问题,请参考以下文章