机器学习-支持向量机SVM算法
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习-支持向量机SVM算法相关的知识,希望对你有一定的参考价值。
文章目录
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。
简介
支持向量机(Support Vector Machine, SVM)对监督学习下二分类问题提供了一个绝妙的解决方案。通过对偶函数和核函数求解,将适用范围从二维线性推广到多维非线性模型,使用相关方法变形,也可用于多分类问题和回归问题。
支持向量机SVM是方法统称,如果应用于分类Classification,也叫支持向量分类SVC;如果应用于回归Regression,也叫支持向量回归SVR。
原理
硬间隔
首先考虑如何评估分类模型的好坏?
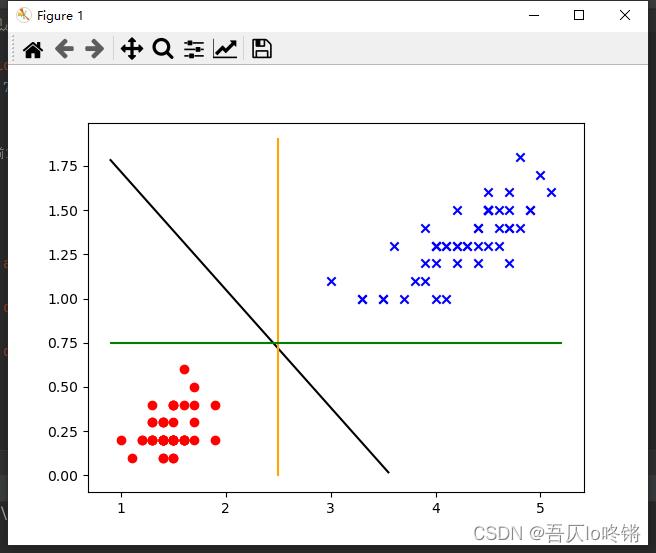
在上图中,红点和蓝叉分别表示两类线性可分的数据(取自鸢尾花数据集)。有黑色、橙色和绿色三个线性模型,都可以将数据分为两类。
直观来说,一般我们会认为黑色表示的分类模型会更好。在SVM中,是因为黑色的间隔最大。所谓的「间隔」,直白的说,就是向垂直方向两边平移,直到遇到数据点,所形成的间隔。
间隔示意图如下所示:
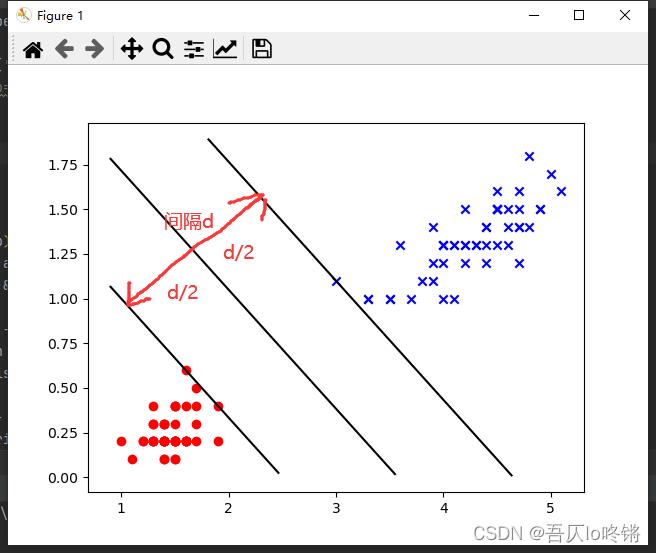
而SVM中认为最佳的模型,就是可以取到最大间隔 d d d的中间那条直线,也就是到两边各是 d 2 \\fracd2 2d,这样就在最大间隔中若干平行线里,唯一确定了最优的线。
如此一来,由于黑色的间隔最大,所以认为优于橙色和绿色所表示的模型。
支持向量
可以看出,在确定最大间隔时,只与少量样本数据有关,平移过程中遇到数据点即停止。我们称这部分样本数据为支持向量,也就是支持向量机名字的由来。这也是支持向量机的一大优势——适用于小样本情况。
以上是二维特征便于可视化的情况。对于二维,我们可以用线来划分;对于三维,我们可以用平面来划分;对于多维,我们称之为超平面,使用超平面来划分。
用如下方程表示超平面:
w
T
x
+
b
=
0
\\bold w^T\\bold x +b =0
wTx+b=0
w
\\bold w
w和
x
\\bold x
x是向量,分别表示权重和特征。
对于二分类任务中,当y=+1是表示正例,y=-1表示负例。也就是y=+1时,
w
T
x
+
b
≥
0
\\bold w^T\\bold x +b \\geq 0
wTx+b≥0,令:
w
T
x
i
+
b
≥
+
1
,
y
i
=
+
1
w
T
x
i
+
b
≤
−
1
,
y
i
=
−
1
\\begincases\\bold w^T\\bold x_i+b \\geq +1,& y_i=+1\\\\ \\bold w^T\\bold x_i+b \\leq -1,& y_i=-1\\endcases
wTxi+b≥+1,wTxi+b≤−1,yi=+1yi=−1
也就是说,上图中三条平行线的表达式分别是 w T x + b = + 1 \\bold w^T\\bold x+b=+1 wTx+b=+1、 w T x + b = 0 \\bold w^T\\bold x+b=0 wTx+b=0、 w T x + b = − 1 \\bold w^T\\bold x+b=-1 wTx+b=−1。
再由点到平面距离公式
r
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
r=\\frac|\\bold w^T \\bold x+b|||\\bold w||
r=∣∣w∣∣∣wTx+b∣,得到间隔(两个异类支持向量到超平面距离)定义:
γ
=
2
∣
∣
w
∣
∣
\\gamma=\\frac2||\\bold w||
γ=∣∣w∣∣2
为了求最大间隔,需要分式中分母最小,即最小化 ∣ ∣ w ∣ ∣ − 1 \\bold ||w||^-1 ∣∣w∣∣−1,等价于最小化 1 2 ∣ ∣ w ∣ ∣ 2 \\frac12||\\bold w||^2 21∣∣w∣∣2。
如此一来,对于线性模型,我们求解如下表达式即可求得最大间隔,也称支持向量机的基本型:
m
i
n
w
,
b
1
2
∣
∣
w
∣
∣
2
s
.
t
.
y
i
(
w
T
x
i
+
b
)
≥
1
\\mathopmin\\limits_\\bold w,b\\quad\\frac12||\\bold w||^2 \\\\ s.t.\\quad y_i(\\bold w^T\\bold x_i+b)\\geq1
w,bmin21∣∣w∣∣2s.t.yi(wTxi+b)≥1
属于二次规划问题,即目标函数二次项,限制条件一次项。使用拉格朗日乘子法可求得其对偶问题,使用对偶问题优化目标函数和限制条件,方便进行求解。
对偶问题
对偶问题(dual problem)简单来说就是同一问题的不同角度解法。比如时间=路程÷速度,那么求最短的时间等价于求最大的速度。
对偶问题定义 L ( w , α , β ) = f ( w ) + α T g ( w ) + β T ( w ) L(w,\\alpha,\\beta)=f(w)+\\alpha^Tg(w)+\\beta^T(w) L(w,α,β)=f(w)+αTg(w)+βT(w)
若 w ∗ w^* w∗是原问题的解, α ∗ \\alpha^* α∗和 β ∗ \\beta^* β∗是对偶问题的解,则有 f ( w ∗ ) ≥ θ ( α ∗ , β ∗ ) f(w^*)\\geq\\theta(\\alpha^*,\\beta^*) f(w∗)≥θ(α∗,β∗)
对约束添加拉格朗日乘子
α
i
≥
0
\\alpha_i\\geq0
αi≥0,
α
i
=
(
α
1
,
α
2
,
…
,
α
m
)
\\alpha_i=(\\alpha_1,\\alpha_2,\\dots,\\alpha_m)
αi=(α1,α2,…,αm)
定义凸二次规划拉格朗日函数:
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
L(\\bold w,b,\\alpha)=\\frac12||\\bold w||^2+\\sum_i=1^m\\alpha_i(1-y_i(\\bold w^T\\bold x_i+b))
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
定义原问题与对偶问题的间距 G G G, G = f ( w ∗ ) − θ ( α ∗ , β ∗ ) ≥ 0 G=f(w^*)-\\theta(\\alpha^*,\\beta^*)\\geq0 G=f(w∗)−θ(α∗,β∗)≥0以上是关于机器学习-支持向量机SVM算法的主要内容,如果未能解决你的问题,请参考以下文章