支持向量机（SVM）|机器学习

Posted 2021-12-03 桃陉

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了支持向量机（SVM）|机器学习相关的知识，希望对你有一定的参考价值。

1.SVM基本原理

1.1特点

$\\bullet$ 支持向量机（Support Vector Machine）主要用于解决模式识别领域中的数据分类问题，属于有监督学习算法的一种。

$\\bullet$ 既可以做分类也可以做回归。

$\\bullet$ 适合于小样本集的场景。

1.2线性二分类问题

比如说对于线性二分类问题来说，我们就是要选择一条直线将两类点进行区分，但是观看下图我们会发现有无数条直线可以做到这一要求，那么我们的选择有什么要求呢？

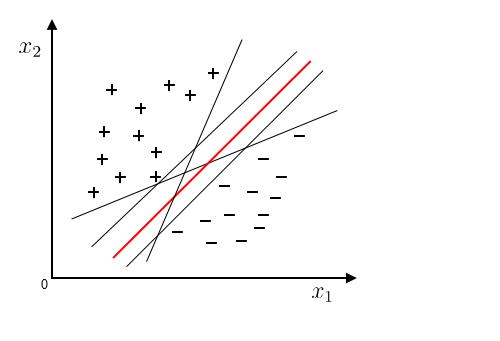
因为这些点都是训练集中的点，而我们最后是要将这一模型使用在测试集上，所以我们就要尽可能选择距离离两类点都较远的直线。选来选去得到的就是位于最中心的那条红线，此时容忍性好，鲁棒性高，泛化能力最强。

1.3间隔与支持向量

在样本空间中，决策边界（超平面）可以通过如下线性方程来描述：

$𝑤^{T}𝑥+𝑏=0$

其中 $𝑤=(𝑤_{1},𝑤_{2},..,𝑤_{𝑑})$ 为法向量，决定了决策边界的方向。 $b$ 为位移项，决定了决策边界与原点之间的距离。显然，决策边界（超平面）可被法向量和位移确定，我们将其表示为 $(w, b)$ 。样本空间中的任意一个点 $x$ ,到决策边界 $(w, b)$ 的距离可写为：

$𝑟=\\frac{|𝑤^{𝑇}𝑥+𝑏|}{||𝑤||}$

假设决策边界 $(w, b)$ 能够将训练样本正确分类，即对于任何一个样本点 $𝑥_{𝑖},𝑦_{𝑖})$ ，若它为正类，即 $𝑦_{𝑖}=+1$ 时， $𝑤^{𝑇}𝑥+𝑏≥+1$ ；若它为负类，即 $𝑦_{𝑖}=−1$ 时， $𝑤^{T}𝑥+𝑏≤−1$ 。即：
$\\left\\{\\begin{matrix} w^{T}x+b \\ge +1,y_{i}=+1; \\\\ w^{T}x+b \\le -1,y_{i}=-1; \\end{matrix}\\right.$

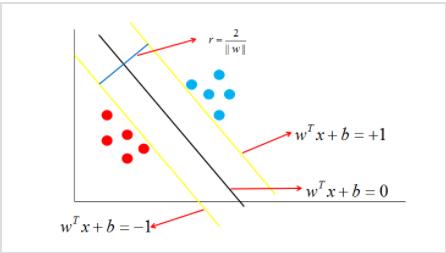
我们可以看到在决策分界两边分别有一条边界，在这两条边界上的点就被称为“支持向量”，而它们(异类支持向量)到决策边界的距离之和就是“间隔”。我们要找的就是具有最大间隔的 $w$ 和 $b$ ，间隔表示为：

$𝑟=\\frac{2}{||𝑤||}$

线性规划方程如下：
$\\left\\{\\begin{matrix} \\underset{w,b}{max} \\ \\frac{2}{||w||} \\\\ s.t. \\ y_{i}(w^{T}x+b)\\ge 1, \\ i=1,2,...m \\end{matrix}\\right.$

1.4核函数

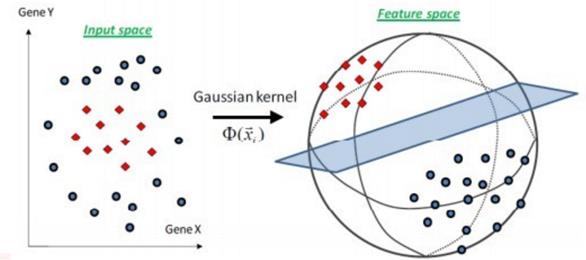
$\\bullet$ 事实上大部分时候数据并不是线性可分的，这个时候满足条件的超平面就根本不存在。对于非线性的情况，SVM处理方法是选择一个核函数，通过将数据映射到高维空间，然后在高维空间中构造最优分离超平面，从而把在低维平面上不好划分的非线性数据分割开来，解决线性不可分的问题。

2.实例

$\\bullet$ 现有数据集中有三列数据，其中前两列未特征值，最后一列为标签值（两种标签）

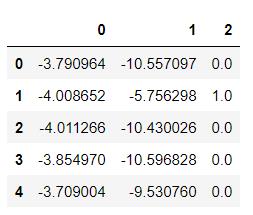
取数据观察

data = pd.read_csv("/data/shixunfiles/5698fb30d8993a1a952de10fc7f0103d_1577667367017.csv")
data.head()

前五列数据如下：

绘制散点图决定使用哪种核函数

#提取特征值和标签值
X = data.iloc[:,:-1].values
y = data.iloc[:,-1].values

#绘制散点图进行观察
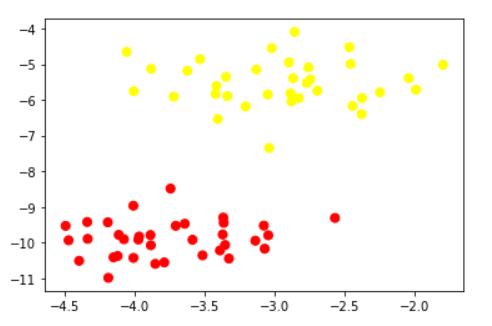
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')

如下图所示，很明显我们可以看到两类样本是线性可分的，所以使用线性核函数linear。

建立并训练模型

from sklearn.svm import SVC #导入支持向量机分类选择器SVC
#建立模型，并训练模型，核函数使用'linear'
model = SVC(kernel='linear')
model.fit(X,y)

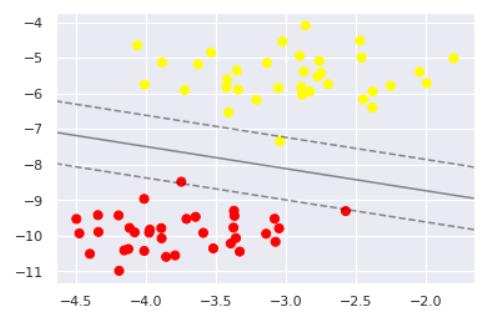
绘制图形查看分类效果

def plot_svc_decision_function(model, ax=None, plot_support=True):
    """为2D SVC绘制决策图"""
    if ax is None:
        ax = plt.gca()
    #获取绘制图表的长和宽，得到两个边界值
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    # 为评估模型画网格线
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    Y, X = np.meshgrid(y, x)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
    
    # 绘制决策边界（等高线图）
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    
    # 绘制支持向量
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0],
                   model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none');
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plot_svc_decision_function(model)