求一个C语言图形变换程序，先进行图形绘制，后能进行图形复制、移动、缩放、旋转，跪求啦。。。

Posted 2023-03-18

从这一部分开始，进入了图形编程的比较烦琐的部分，要真正对图形编程有所了解，这一部分的内容是必须要掌握的。

在计算机绘图过程中，经常需要进行绘图变换，主要包括二维图形变换和三维图形变换。这一部分讨论二维图形变换，其内容有用户坐标到屏幕坐标的变换、图形的比例变换、对称变换、错切变换、旋转变换、平移变换和复合变换等。后面讲到了二维剪裁，即线段裁剪与多边形裁剪。

第一节 用户坐标到屏幕坐标变换

假设纸上有一个图形，要用计算机把它在屏幕上画出来。那么首先遇到的问题是，纸上的图形采用的坐标是实数域域中的直角坐标系或是极坐标系，统称为用户坐标系。而屏幕上采用的坐标系是整数域中直角坐标系，这类坐标系统称为设备坐标系。因此用户坐标系中图形需要经过变换才能绘制在屏幕上，显然这个变换的内容包括： 1)将用户坐标系中任意范围区域转换到屏幕某个范围区域，从而用户坐标系此范围区域内的图形也转换到屏幕上该范围区域内。 2)用户坐标系此区域内图形上的坐标值转换到屏幕上该范围区域内后不一定是整数，取整后才成为该范围区域内的屏幕坐标值。 3)用户坐标右手系到屏幕坐标左手系的坐标轴方向变换。 4)当屏幕坐标系水平方向与垂直方向刻度不等(即像素间距不等)时，为保持图形不走样，还要进行比例变换。下面介绍这些内容的具体计算问题。

1.窗口到视口的变换

更确切地说，是实际图形到屏幕图形的转换。有时也称为数据规格化。

在用户坐标系中，指定一矩形域以确定要显示(或绘制)的图形部分，这个矩形区域称为窗口。在屏幕上可任选一矩形域以显示(或绘制)窗口内的图形，该域称为视口。如图2-1所示。

一般视窗口的四条边界分别为：

左边界 x=x1、右边界 x=x2.下边界 y=y1,上边界y=y2。

视口的四条边界分别为：

左边界sx=sx1,右边界sx=sx2,上边界sy=sy1,下边界sy=sy2。

经变换后应有，窗口的上边界线段(或下边界线段)长x2-x1变换成视口上边界线段(或下边界线段)长sx2-sx1。设其比例变换因子为k1，则可得

k1*(x2-x1)=sx2-sx1

k1=(sx2-sx1)/(x2-x1)

对窗口内任一x坐标(x1<=x<=x2)变换后为视口内水平方向sx坐标(sx1<=sx<=sx2)。由上述有：

k1*(x-x1)=sx-sx1

sx=sx1+k1*(x-x1)

=sx1+(x-x1)*(sx2-sx1)/(x2-x1)

同样，经变换后窗口的左边界线段(或右边界线段)长y2-y1变换成视口左边界线段(或右边界线段)长sy2-sy1。设其比例变换因子为k2，则可得

k2*(y2-y1)=sy2-sy1

k2=(sy2-sy1)/(y2-y1)

对窗口内任一y坐标(y1<=y<=y2)变换后为视口内垂直sy坐标(sy1<=sy<=sy2)，应有

k2*(y-y1)=sy-sy1

sy=sy1+k2*(y-y1)

=sy1+(y-y1)*(sy2-sy1)/(y2-y1)

于是对窗口内图形上任一点坐标(x,y)变换到屏幕上视口内成为(sx,sy)，则

sx=sx1+(x-x1)*(sx2-sx1)/(x2-x1)

sy=sy1+(y-y1)*(sy2-sy1)/(y2-y1)

写成简式

sx=k1*x+a

sy=k2*y+b

这里

a=sx1-k1*x1

b-sy1-k2*y1

k1=(sx2-sx1)/(x2-x1)

k2=(sy2-sy1)/(y2-y1)

2. 实型值到整型值的变换

上面对窗口内图形上任一点坐标(x,y)变换到屏幕上视口内成为(sx,sy)，

sx=k1*x+a

sy=k2*y+b k1,k2,a,b同上

这样计算出来的sx,sy一般是实型值，而屏幕上视口内屏幕坐标是整型值，因此要将sx,sy实型值转换成屏幕坐标系的整型值。这可以通过四舍五入的方法将实型值的绝对值圆整化。由于C语言中已经替我们想到了这点，它提供的函数可以自动取整，因此用户在调用标准函数在屏幕上绘图时一般不需要考虑这个问题。当然也可以用赋值的类型转换规则来实现实型值到整型值的变换。

3. y坐标值方向变换

一般屏幕坐标系是直角左手系，y轴方向向下为正，原点在屏幕的左上角，如图2-2所示。

窗口内图形上任一点(x,y)变换到视口内成为(sx,xy)，而(x,y)是相对用户坐标系(直角右手系)的。(sx,sy)是相对屏幕坐标系(直角左手系)的，因此y轴方向相反。为使窗口内图形变换到视口上图形其形状一致，需将视口上图形y轴方向变换成窗口内图形y轴方向。这只要将求得的视口内各点的sy整型坐标均用sy2去减，即sy2-sy(整型)代替sy(整型)即可，经这样的坐标轴方向变换后得到的视口内图形与窗口内图形一致。

4.长宽比例变换

屏幕坐标系x方向与y方向上的刻度可能不一样，这取决于水平方向像素间距与垂直方向偈素间距大小是否一致。如果两个方向的刻度不相等，那么用户坐标系下一个正方形将显示(或绘制)成为一个长方形有，一个圆将成为一个椭圆。

为保持原图形的长宽比。使图形显示(或绘制)后不走样，需求出屏幕上两侍标轴刻度的比值(即纵横比)。可以用函数getaspectratio()(见前文所述)返回x方向和y方向的比例数，从而求得这个比值。再瘵原图形y方向坐标乘以该比值，这样显示(或绘制)出来的图形应不走样。若不考虑图形的走样，就不必作这个变换。

第二节 二维几何变换

图形的几何变换一般是指对图形的几何信息经过变换后产生新的图形，图形几何变换既可以看作是坐标系不动而图形变动，变动后的图形在坐标系中的坐标值发生变化；出可以看作图形不动而坐标系变动，变动后的图形在新坐标系下具有新的坐标值。这两种情况本质上都是一样的，都是图形由新的坐标值表示，因此是新产生的图形。图形几何变换包括比例变换、对称变换、错切变换、旋转变换、平移变换及其复合变换。图形上所有的点在几何变换前后的坐标关系一般用解析几何方法可以求得，但这些几何关系用矩阵方法表示，运算更为方便。

一、基本变换

图形基本几何变换是指比例变换、对称变换、错切变换、旋转变换和平移变换等。除平移变换外，这里其它四种几何变换都可以用组成图形的点向量(或称1×2阶矩阵)和2×2阶变换矩阵相乘表示，而平移变换需引入新方法来实现。

1、比例变换

设图形上一点P(x,y)，经比例变换后成为新的菜上一点P'(x',y')，即有

x'=a*x

y'=d*y

式中a,d为比例因子

将此比例变换式写成矩阵式得

a 0

[x' y']=[x y] = [x y] * T

0 d

a 0

这里 T= 叫做比例变换矩阵。若a=d，则x,y坐标按同一比例变换。

0 d

当a=d>1时，图形放大；当0<a=d<1时，图形缩小。

若a≠d，则x,y坐标按各自不同比例变换。

3 0

例 1： 设有比例变换矩阵 T= , 三角形abc经过比例变换成为三角形a'b'c'。

0 1

如图2-3所示。

3 0

a [1 2] = [3 2] a'

0 1

3 0

b [2 2] = [6 2] b'

0 1

3 0

c [2 3] = [6 3] c'

0 1

2. 对称变换

图形上一点P(x,y)经关于原点对称变换后成为新图形上一点P'(x',y')，则

x' = -x

y' = -y

写成矩阵形式成为

-1 0

[x' y'] = [x y] = [x y] * T

0 -1

-1 0

这里 T = 为关于原点对称变换矩阵。

0 -1

若关于x轴对称，则对称变换的矩阵表示为

1 0

[x' y'] = [x y] = [x y] * T

0 -1

1 0

于是关于x轴对称变换矩阵 T =

0 -1

若关于y轴对称，则对称变换的矩阵表示为

-1 0

[x' y'] = [x y] = [x y] * T

0 1

-1 0

于是关于y轴对称变换矩阵 T =

0 1

若关于直线y = -x对称，则对称变换矩阵表示为

0 -1

[x' y'] = [x y] = [x y] * T

-1 0

0 1

于是关于直线 y = x对称变换矩阵 T =

1 0

各种对称变换的图形均可由实例程序绘出，参见实例程序图形。

3. 错切变换

对图形的任一点P(x,y)，作线性变换如下

x' = x + by

y' = y + dx

式中b,d为不全为零的常 数，点P'(x',y')为新图形上相应的点，这个变换称为图形的错切变换。

错切变换的矩阵表示为

1 d

[x' y'] = [x y] = [x y] * T

b 1

1 d

T = 叫做错切变换矩阵(b,d不全为零)。

b 1

① 当d=0时，x'=x+by,y'=y，这时图形的y坐标不变，x坐标值随(x,y)及系数b作线性变化。若b>0时，图形沿x轴作错切位移；若b<0，图形沿x轴负向作错切位移。

② 当b=0时，x'=x,y'=dx+y，此时图形的x坐标不变y坐标随(x,y)及系数d作线性变化。如d>0，图形沿y轴正向作错切位移；如d<0，图形沿y轴负向作错切位移。

③ 当b≠0且d≠0时，x'=x+by,y'=y+dx，图形沿x,y两个方向作错切位移。

1 2

例 2： 设有错切变换 矩阵 T = ，正方形abcd经此错切变换成为四边形a'b'c'd'，

0 1

如图2-4所示。

1 2

a [0 0] = [0 0] a'

0 1

1 2

b [1 0] = [1 2] b'

0 1

1 2

c [1 1] = [1 3] c'

0 1

1 2

d [0 1] = [0 1] d'

0 1

4. 旋转变换

设图形上一点P(x,y)绕原点逆时针旋转θ角后成为新的图形上一点P'(x',y')，则由解析几何方法可得

x' = xcosθ + ysinθ

y' = -xsinθ + ycosθ

用矩阵表示为

cosθ -sinθ

[x' y'] = [x y] = [x y] * T

sinθ cosθ

cosθ -sinθ

这里 T = 为绕原点逆时针变换矩阵。若顺时针旋转时，θ角为负值。

sinθ cosθ

5. 平移变换

若图形上一点P(x,y)沿x轴平移 l距离，沿y轴平移m距离后成为新的图形上一点P'(x',y')，则有

x' = x + l

y' = y + m

式中l,m不全为零，这称为平移变换。但此变换无法用组成图形的点向量和2×2阶变换矩阵相乘来实现。

用二维点向量和2×2阶矩阵相乘不能表示图形的平移变换，那么自然会想到用三维点向量和3×3阶矩阵相乘来实现图形的平移变换。因此对图形上二个坐标的点向量需要添加一个坐标，使之成为三维点向量以便与三阶矩阵相乘，进而实现用矩阵表示平移变换。实际上就是对上面的二个坐标变换式添加第三个坐标变换式，即成为

x' = x + l

y' = y + m

k = k

这第三个坐标变换式(即k=k)必须是恒等式，因为不需作变换，本质上是为了进行矩阵运算而引入的。

将此三个变换式(仍然是图形的平移变换，不妨将k = k取成1=1)写成矩阵得

1 0 0

[x' y' l] = [x y l] 0 1 0 = [x y 1] * T

l m 1

1 0 0

显然 T = 0 1 0 为图形的平移变换矩阵。

l m 1

这里通过对原图形上二维点向量引进第三个坐标成为三维点向量，从而使原图形的平移变换 能用矩阵表示。同样其它基本变换也可以如此用矩阵表示。因此图形的基本变换都可以在这样的三维点向量下统一、整齐用矩阵表示。这样的三维点向量称为齐次点向量，也叫三维齐次坐标点，简称三维齐次坐标。只有在三维齐次坐标下，二维几何变换才都可以用矩阵表示。下面再进一步讨论一下齐次坐标的优点。

引用齐次坐标后，可将上面各种基本变换矩阵统一在一个三阶矩阵中。即

a b 0

T = c d 0

l m 1

式中左上角二阶矩阵实现比例、对称、错切、旋转等变换，左下角1×2阶矩阵实现平移变换，其中a,b,c,d,l,m只要赋以相应的值，并建立图形上点的齐次坐标(即在图形上点的坐标后引入第三个坐标1)，这样就可以用图形上点的三维齐次坐标与此三阶矩阵相乘来表示三维图形的基本几何变换了。而变换后，不用考虑第三个坐标1，前面两个坐标就反映了图形的整个变换情况。

用齐次坐标表示一个图形上的点，可以有多种表示，如(6,8，1)、(12,16,2)、(30,40,5)等均表示图形上同一个点(6,8)。这样，齐次坐标可以表示计算机无法容纳的数。例如当计算机的字长为16位时，它能表示的最大整数为216-1=32767。若点坐标为(80 000,40 000)，则计算机无法表示。但用齐次坐标可表示为(20 000,10 000,1/4)，经过处理后再用第三个坐标支除前面两个坐标，从而得到原来通常的坐标。

齐次坐标优点很多，在计算机绘图中都采用这种表示来处理图形。下面介绍的图形复合几何变换就是如此。

二、复合变换

图形的复合几何变换是指图形作一次以上的基本几何变换，变换结果是每次基本变换矩阵的乘积。图殂的复合几何变换简称复合变换。

1. 复合平移

若对图形首先作平移变换 T1，然后再作平移变换T2，相应的平移变换矩阵分别为

1 0 0

T1 = 0 1 0

l1 m1 1

1 0 0

T2 = 0 1 0

l2 m2 1

则变换结果为复合平移变换T，其复合平移变换矩阵为

T = T1 * T2

1 0 0 1 0 0

= 0 1 0 * 0 1 0

l1 m1 1 l2 m2 1

1 0 0

= 0 1 0

l1+l2 m1|m2 1 参考技术A PHotoshop快捷健:
PHOTOSHOP热键一览表,工具箱(多种工具共用一个快捷键的可同时按加此快捷键选取) 矩形、椭圆选框工具 || 裁剪工具 ||
移动工具 ||套索、多边形套索、磁性套索
〓正文〓
工具箱(多种工具共用一个快捷键的可同时按加此快捷键选取)
矩形、椭圆选框工具
裁剪工具
移动工具
套索、多边形套索、磁性套索
魔棒工具
喷枪工具
画笔工具
像皮图章、图案图章
历史记录画笔工具
像皮擦工具
铅笔、直线工具
模糊、锐化、涂抹工具
减淡、加深、海棉工具
钢笔、自由钢笔、磁性钢笔
添加锚点工具
删除锚点工具
直接选取工具
文字、文字蒙板、直排文字、直排文字蒙板
度量工具
直线渐变、径向渐变、对称渐变、角度渐变、菱形渐变
油漆桶工具
吸管、颜色取样器
抓手工具
缩放工具
默认前景色和背景色
切换前景色和背景色
切换标准模式和快速蒙板模式
标准屏幕模式、带有菜单栏的全屏模式、全屏模式
临时使用移动工具
临时使用吸色工具
临时使用抓手工具
打开工具选项面板
快速输入工具选项(当前工具选项面板中至少有一个可调节数字) 至
循环选择画笔 或
选择第一个画笔 +
选择最后一个画笔 +
建立新渐变(在”渐变编辑器”中) +
文件操作
新建图形文件 +
用默认设置创建新文件 ++
打开已有的图像 +
打开为... ++
关闭当前图像 +
保存当前图像 +
另存为... ++
存储副本 ++
页面设置 ++
打印 +
打开“预置”对话框 +
显示最后一次显示的“预置”对话框 ++
设置“常规”选项(在预置对话框中) +
设置“存储文件”(在预置对话框中) +
设置“显示和光标”(在预置对话框中) +
设置“透明区域与色域”(在预置对话框中) +
设置“单位与标尺”(在预置对话框中) +
设置“参考线与网格”(在预置对话框中) +
设置“增效工具与暂存盘”(在预置对话框中) +
设置“内存与图像高速缓存”(在预置对话框中) +
编辑操作
还原/重做前一步操作 +
还原两步以上操作 ++
重做两步以上操作 ++
剪切选取的图像或路径 +或 拷贝选取的图像或路径 +
合并拷贝 ++
将剪贴板的内容粘到当前图形中 +或
将剪贴板的内容粘到选框中 ++
自由变换 +
应用自由变换(在自由变换模式下)
从中心或对称点开始变换 (在自由变换模式下)
限制(在自由变换模式下)
扭曲(在自由变换模式下)
取消变形(在自由变换模式下)
自由变换复制的象素数据 ++
再次变换复制的象素数据并建立一个副本 +++
删除选框中的图案或选取的路径
用背景色填充所选区域或整个图层 +或+
用前景色填充所选区域或整个图层 +或+
弹出“填充”对话框 +
从历史记录中填充 ++ 图像调整
调整色阶 +
自动调整色阶 ++
打开曲线调整对话框 +
在所选通道的曲线上添加新的点(‘曲线'对话框中) 在图象中加点按
在复合曲线以外的所有曲线上添加新的点(‘曲线'对话框中) +
加点按
移动所选点(‘曲线'对话框中) ///
以10点为增幅移动所选点以10点为增幅(‘曲线'对话框中) +
选择多个控制点(‘曲线'对话框中) 加点按
前移控制点(‘曲线'对话框中) +
后移控制点(‘曲线'对话框中) ++
添加新的点(‘曲线'对话框中) 点按网格
删除点(‘曲线'对话框中) 加点按点
取消选择所选通道上的所有点(‘曲线'对话框中) +
使曲线网格更精细或更粗糙(‘曲线'对话框中) 加点按网格
选择彩色通道(‘曲线'对话框中) +
选择单色通道(‘曲线'对话框中) +
打开“色彩平衡”对话框 +
打开“色相/饱和度”对话框 +
全图调整(在色相/饱和度”对话框中) +
只调整红色(在色相/饱和度”对话框中) +
只调整黄色(在色相/饱和度”对话框中) +
只调整绿色(在色相/饱和度”对话框中) +
只调整青色(在色相/饱和度”对话框中) +
只调整蓝色(在色相/饱和度”对话框中) +
只调整洋红(在色相/饱和度”对话框中) +
去色 ++
反相 +
图层操作
从对话框新建一个图层 ++
以默认选项建立一个新的图层 +++
通过拷贝建立一个图层 +
通过剪切建立一个图层 ++
与前一图层编组 +
取消编组 ++
向下合并或合并联接图层 +
合并可见图层 ++
盖印或盖印联接图层 ++
盖印可见图层 +++
将当前层下移一层 +
将当前层上移一层 +
将当前层移到最下面 ++
将当前层移到最上面 ++
激活下一个图层 +
激活上一个图层 +
激活底部图层 ++
激活顶部图层 ++
调整当前图层的透明度(当前工具为无数字参数的,如移动工具) 至
保留当前图层的透明区域(开关)
投影效果(在”效果”对话框中) +
内阴影效果(在”效果”对话框中) +
外发光效果(在”效果”对话框中) +
内发光效果(在”效果”对话框中) +
斜面和浮雕效果(在”效果”对话框中) +
应用当前所选效果并使参数可调(在”效果”对话框中)
图层混合模式
循环选择混合模式 +或
正常 ++
阈值（位图模式） ++
溶解 ++
背后 ++
清除 ++
正片叠底 ++
屏幕 ++
叠加 ++
柔光 ++
强光 ++
颜色减淡 ++
颜色加深 ++
变暗 ++
变亮 ++
差值 ++
排除 ++
色相 ++
饱和度 ++
颜色 ++
光度 ++
去色 海棉工具+++
加色 海棉工具+++
暗调 减淡/加深工具+++
中间调 减淡/加深工具+++
高光 减淡/加深工具+++
选择功能
全部选取 +
取消选择 +
重新选择 ++
羽化选择 ++
反向选择 ++
路径变选区 数字键盘的
载入选区 +点按图层、路径、通道面板中的缩约图
滤镜
按上次的参数再做一次上次的滤镜 +
退去上次所做滤镜的效果 ++
重复上次所做的滤镜(可调参数) ++
选择工具(在“3D变化”滤镜中)
立方体工具(在“3D变化”滤镜中)
球体工具(在“3D变化”滤镜中)
柱体工具(在“3D变化”滤镜中)
轨迹球(在“3D变化”滤镜中)
全景相机工具(在“3D变化”滤镜中)
视图操作
显示彩色通道 +
显示单色通道 +
显示复合通道
以CMYK方式预览(开关) +
打开/关闭色域警告 ++
放大视图 +
缩小视图 +
满画布显示 +
实际象素显示 ++
向上卷动一屏
向下卷动一屏
向左卷动一屏 +
向右卷动一屏 +
向上卷动10 个单位 +
向下卷动10 个单位 +
向左卷动10 个单位 ++
向右卷动10 个单位 ++
将视图移到左上角
将视图移到右下角
显示/隐藏选择区域 +
显示/隐藏路径 ++
显示/隐藏标尺 +
显示/隐藏参考线 +
显示/隐藏网格 +
贴紧参考线 ++
锁定参考线 ++
贴紧网格 ++
显示/隐藏“画笔”面板
显示/隐藏“颜色”面板
显示/隐藏“图层”面板
显示/隐藏“信息”面板
显示/隐藏“动作”面板
显示/隐藏所有命令面板
显示或隐藏工具箱以外的所有调板 +
文字处理(在”文字工具”对话框中)
左对齐或顶对齐 ++
中对齐 ++
右对齐或底对齐 ++
左／右选择 1 个字符 +/
下／上选择 1 行 +/
选择所有字符 +
选择从插入点到鼠标点按点的字符 加点按
左／右移动 1 个字符 /
下／上移动 1 行 /
左／右移动1个字 +/
将所选文本的文字大小减小2 点象素 ++
将所选文本的文字大小增大2 点象素 ++
将所选文本的文字大小减小10 点象素 +++
将所选文本的文字大小增大10 点象素 +++
将行距减小2点象素 +
将行距增大2点象素 +
将基线位移减小2点象素 ++
将基线位移增加2点象素 ++
将字距微调或字距调整减小20/1000ems +
将字距微调或字距调整增加20/1000ems +
将字距微调或字距调整减小100/1000ems ++
将字距微调或字距调整增加100/1000ems ++
选择通道中白的像素（包括半色调）++

在Layers、Channels、Paths调色板上，按Alt单击这些调色板底部的工具图标时，对于有对话框的工具可调出相应的对话框来更改设置。
移动图层和选取框时，按住Shift键可做水平、垂直或45度角的移动，按键盘上的方向键可做每次lpixel的移动，按住Shift 键再按键盘上的方向键可做每次10pixel的移动。

在使用选取工具时，按Shift键拖动鼠标可以在原选取框外增加选取范围（开集）；按Alt键拖动鼠标可以删除与原选取框重叠部分的选取范围；同时按Shift与Alt键拖动鼠标可以选取与原选取框重叠的范围（交集）。

调用Curves对话框时，按住Alt键于格线内单击鼠标可以增加网格线，提高曲线精度。
更改某一对话框的设置后，若要恢复为默认值，只要按住Alt键，Cancel键会变成Reset键，在Reset键上单击即可。
若要将某一图层上的图像拷贝到尺寸不同的图像窗口中央位置时，可以在拖动鼠标的同时按住Shift键，图像拖动到目的窗口后会自动居中。
若要将图像用于网络传输，可将图像模式设置为Indexed Color索引色彩色模式，有文件小、传输快的优点，如果再选择GIF89a Export(GIF输出），可以设置透明的效果，并将文件保存成GIF格式。

在使用自由变形（Layer/Free Transform）功能时，按Ctrl键并拖动某一控制点可以进行随意变形的调整；“Shift+Ctrl”键并拖动某一控制点可以进行倾斜调整；按Alt键并拖动某一控制点可以进行对称调整；按“Shift+Ctrl+Alt”键并拖动某一控制点可以进行透视效果的调整。

在layers调色板上，按住Ctrl用鼠标单击某一图层时，可载入该层图像成选取框(Background层除外，改名后可以）。
使用路径(Path)工具时的几个技巧：使用笔形(Pen)工具制作路径时按住Shift键可以强制路径或方向线成水平、垂直或45度角，按住Ctrl键可暂时切换到路径选取工具，按住Alt键将笔形光标在在黑色节点上单击可以改变方向线的方向，使曲线能够转折；按Alt键用路径选取(Direct
Selection)工具单击路径会选取整个路径；要同时选取多个路径可以按住Shift后逐个单击；使用路径选工具时按住“Ctrl+Alt”键移近路径会切换到加节点与减节点笔形工具。

若要切换路径(path)是否显示，可以按住Shift键后在路径调色板的路径栏上单击鼠标, 或者在路径调色版灰色区域单击即可.
若要一起执行数个宏(Action),可以先增加一个宏，然后录制每一个所要执行的宏。 若要在一个宏(Action)中的某一命令后新增一条命令，可以先选中该命令，然后单击调色板上的开始录制(Begin recording)图标，选择要增加的命令，再单击停止录制(Stop
recording)图标即可。

使用Filter/Render/Clouds滤镜时，若要产生更多明显的支纹图案，可先按住Alt键后再执行该命令；若要生成低漫射支彩效果，可先按住Shift键后再执行命令。

在使用Filter/Render/Lighting Effects滤镜时，若要在对话框内复制光源时，可先按住Alt键后再拖动光源即可实现复制。
若要在Color调色板上直接切换色彩模式，可先按住Shift键后，再将光标移到色彩条上单击即可。

3D MAX快捷健:
显示降级适配（开关）
适应透视图格点 ++
排列 +
角度捕捉(开关)
动画模式 (开关)
改变到后视图
背景锁定(开关) ++
前一时间单位
下一时间单位
改变到上（Top）视图
改变到底(Bottom)视图
改变到相机(Camera)视图
改变到前（Front）视图
改变到等大的用户(User)视图
改变到右(Right)视图
改变到透视（Perspective）图
循环改变选择方式 +
默认灯光(开关) +
删除物体
当前视图暂时失效
是否显示几何体内框(开关) +
显示第一个工具条 +
专家模式�全屏(开关) +
暂存(Hold)场景 ++
取回(Fetch)场景 ++
冻结所选物体
跳到最后一帧
跳到第一帧
显示/隐藏相机（Cameras） +
显示/隐藏几何体(Geometry) +
显示/隐藏网格(Grids)
显示/隐藏帮助(Helpers)物体 +
显示/隐藏光源(Lights) +
显示/隐藏粒子系统(Particle Systems) +
显示/隐藏空间扭曲(Space Warps)物体 +
锁定用户界面(开关) +
匹配到相机(Camera)视图 +
材质(Material)编辑器
最大化当前视图 (开关) +
脚本编辑器
新的场景 +
法线(Normal)对齐 +
向下轻推网格 小键盘
向上轻推网格 小键盘
NURBS表面显示方式 +或+
NURBS调整方格1 +
NURBS调整方格2 +
NURBS调整方格3 +
偏移捕捉 ++
打开一个MAX文件 +
平移视图 +
交互式平移视图
放置高光(Highlight) +
播放/停止动画
快速(Quick)渲染 +
回到上一场景*作 +
回到上一视图*作 +
撤消场景*作 +
撤消视图*作 +
刷新所有视图
用前一次的参数进行渲染 +或
渲染配置 +或
在xy/yz/zx锁定中循环改变
约束到X轴
约束到Y轴
约束到Z轴
旋转(Rotate)视图模式 +或
保存(Save)文件 +
透明显示所选物体(开关) +
选择父物体
选择子物体
根据名称选择物体
选择锁定(开关)
减淡所选物体的面(开关)
显示所有视图网格(Grids)(开关) +
显示/隐藏命令面板
显示/隐藏浮动工具条
显示最后一次渲染的图画 +
显示/隐藏主要工具栏 +
显示/隐藏安全框 +
*显示/隐藏所选物体的支架
显示/隐藏工具条 /
百分比(Percent)捕捉(开关) ++
打开/关闭捕捉(Snap)
循环通过捕捉点 +
声音(开关) 【】
间隔放置物体 +
改变到光线视图 +
循环改变子物体层级
子物体选择(开关) +
帖图材质(Texture)修正 +

全部解冻
根据名字显示隐藏的物体
刷新背景图像(Background) +++
显示几何体外框(开关)
视图背景(Background) +

用方框(Box)快显几何体(开关) +
打开虚拟现实 数字键盘
虚拟视图向下移动 数字键盘
虚拟视图向左移动 数字键盘
虚拟视图向右移动 数字键盘
虚拟视图向中移动 数字键盘
虚拟视图放大 数字键盘
虚拟视图缩小 数字键盘
实色显示场景中的几何体(开关)
全部视图显示所有物体 ++
*视窗缩放到选择物体范围（Extents）
缩放范围 ++
视窗放大两倍 +数字键盘
放大镜工具
视窗缩小两倍 +数字键盘
根据框选进行放大 +

加入(Add)关键帧

编辑(Edit)关键帧模式
编辑区域模式
编辑时间模式
展开对象（Object）切换
展开轨迹（Track）切换
函数(Function)曲线模式 或
锁定所选物体
向上移动高亮显示
向下移动高亮显示
向左轻移关键帧
向右轻移关键帧
位置区域模式

向下收拢 +
向上收拢 +

下一时间单位
前一时间单位
回到上一场景*作 +
撤消场景*作 +

绘制(Draw)区域
渲染(Render)
锁定工具栏(泊坞窗)

加入过滤器(Filter)项目 +
加入输入(Input)项目 +
加入图层(Layer)项目 +
加入输出(Output)项目 +
加入(Add)新的项目 +
加入场景(Scene)事件 +
编辑(Edit)当前事件 +
执行(Run)序列 +
新(New)的序列 +
撤消场景*作 +

CV 约束法线(Normal)移动 +
CV 约束到U向移动 +
CV 约束到V向移动 +
显示曲线(Curves) ++
显示控制点(Dependents) +
显示格子(Lattices) +
NURBS面显示方式切换 +
显示表面(Surfaces) ++
显示工具箱(Toolbox) +
显示表面整齐(Trims) ++
根据名字选择本物体的子层级 +
锁定2D 所选物体
选择U向的下一点 +
选择V向的下一点 +
选择U向的前一点 +
选择V向的前一点 +
根据名字选择子物体
柔软所选物体 +
转换到Curve CV 层级 ++
转换到Curve 层级 ++
转换到Imports 层级 ++
转换到Point 层级 ++
转换到Surface CV 层级 ++
转换到Surface 层级 ++
转换到上一层级 ++
转换降级 +

转换到控制点(Control Point)层级 ++
到格点(Lattice)层级 ++
到设置体积(Volume)层级 ++
转换到上层级 ++

进入编辑(Edit)UVW模式 +
调用*.uvw文件 +++
保存UVW为*.uvw格式的文件 +++
打断(Break)选择点 +
分离(Detach)边界点 +
过滤选择面 +
水平翻转 +++
垂直(Vertical)翻转 +++
冻结(Freeze)所选材质点 +
隐藏(Hide)所选材质点 +
全部解冻(unFreeze) +
全部取消隐藏(unHide) +
从堆栈中获取面选集 +++
从面获取选集 +++

水平镜象 +++
垂直镜象 +++
水平移动 +++
垂直移动 +++
平移视图 +
象素捕捉
平面贴图面/重设UVW +++
水平缩放 +++
垂直缩放 +++
移动材质点
旋转材质点
等比例缩放材质点
焊接(Weld)所选的材质点 ++
焊接(Weld)到目标材质点 +
Unwrap的选项(Options) +
更新贴图(Map) +++
将Unwrap视图扩展到全部显示 ++
框选放大Unwrap视图 +
将Unwrap视图扩展到所选材质点的大小 +++
缩放到Gizmo大小 +
缩放(Zoom)工具

建立(Create)反应(Reaction) ++
删除(Delete)反应(Reaction) ++
编辑状态(State)切换 ++
设置最大影响(Influence) +
设置最小影响(Influence) +
设置影响值(Value) ++

初始化
更新

MAXScript收听器 F11
NURBS镶嵌预设1 Ctrl+1
NURBS镶嵌预设2 Ctrl+2
NURBS镶嵌预设3 Ctrl+3
NURBS阴影网格开关 Alt+L, Ctrl+4
按名称取消隐藏 5
百分比捕捉(开关) Shift+Ctrl+P
保持 Alt+Ctrl+H
保存文件 Ctrl+S
备份一单位时间 , 背景锁定(开关) Alt+Ctrl+B
边界面开关 F4
变换标志框（开关） X
变换标志框大小- -
变换标志框大小+ =
变换标志框卷标（开关） 变换标志框平面（开关） 变换标志框中心（开关） 变换输入 F12 播放动画 / 捕捉(?/pre>

分享给你的朋友吧：

对我有帮助
1

回答时间：2006-3-30 13:29
|

回答者：

|

擅长领域：

暂未定制

参加的活动：

暂时没有参加的活动

提问者对于答案的评价：
首先谢谢各位。但我只能给一个人加分

WebGL学习系列-基本图形变换

前言

经过前面的学习，我们已经可以绘制基本的图形了。本小节将介绍基本的图形变换，介绍在WebGL中，如何对基本的图形进行平移、旋转和缩放。

平移

在前面的小节中，我们已经绘制过一个三角形，那时候，它看起来是这样的：

我们知道，在WebGL中，要绘制一个基本的图形，我们只需要指定顶点的位置、大小和颜色，然后调用drawArrays接口进行绘制即可。现在，我们想要实现对三角形进行一个平移，比如，把它移到右上角的地方，那如何实现呢？

其实仔细想想，你会发现，我们要移动一个三角形，只需要移动它的三个顶点即可，然后WebGL将会自动在新的顶点位置把三角形绘制出来。

其原理示意图如下：

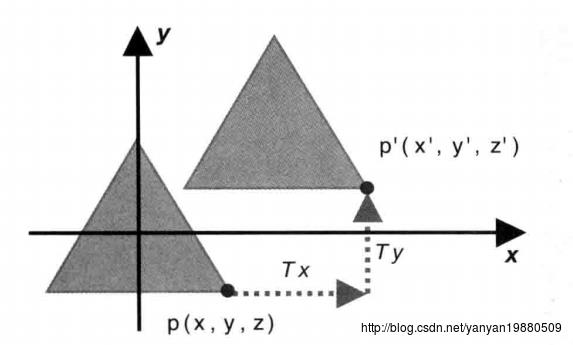
为了进一步说明在程序中是如何实现平移的，我们先来看下顶点着色器代码：

// 顶点着色器代码(决定顶点的位置、大小、颜色)
var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\\n' +
  'uniform vec4 u_Translation;\\n' +
  'void main() \\n' +
  '  gl_Position = a_Position + u_Translation;\\n' + // 设置顶点的位置
  '  gl_PointSize = 10.0;\\n' +      // 设置顶点的大小
  '\\n';

主要看到两个地方有所变动 ：
1、添加了 uniform vec4 u_Translation 定义
2、顶点的位置使用两个 vec4 变量进行相加， gl_Position = a_Position + u_Translation

我们以前曾经使用过 attribute变量，用于直接表示顶点的位置，那时我们知道每个顶点的位置都不一样，而现在，为了对三角形进行平移，实际上是对三个顶点都进行了相同的平移，也就是说，平移的量对所有顶点是一致的，这样所有顶点共享的变量在WebGL中使用uniform 关键字进行表示。

既然定义了 uniform 变量，那么就需要对它进行赋值，对它的赋值跟对 attribute变量进行赋值的流程是完全一样的。

// 三角形顶点的平移量
var Tx = 0.5, Ty = 0.5, Tz = 0.0;
var u_Translation = context.getUniformLocation(context.program,'u_Translation');
context.uniform4f(u_Translation, Tx, Ty, Tz, 0.0);

我们定义了 Tx，Ty，Tz 表示顶点在x、y、z 轴上的位移，最后使用 uniform4f 方法对 u_Translation变量进行了赋值，这里有个地方要注意，方法 uniform4f 最后一个参数我们设置为了0.0，因为我们要确保两个vec4变量相加后，第四个参数为1。a_Position 变量第四个参数已经设置为1，所以u_Translation第四个参数只能设置为0。

最后，我们来看下平移后的效果图：

旋转

旋转看起来比平移要复杂一些，在考虑旋转的时候，我们要考虑三个点：

1. 绕着哪个轴旋转
2. 旋转的方向（顺时针还是逆时针）
3. 旋转的角度

在这里，我们以绕着Z轴逆时针旋转来推导

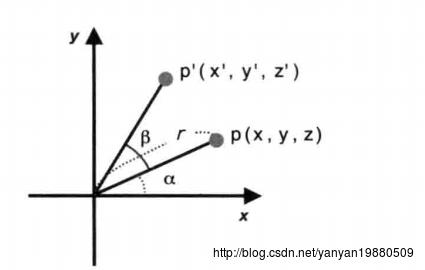
由上图可以看到，当一个点$p\\left ( x,y,z \\right )$沿着Z轴逆时针旋转到$p\'\\left ( x\',y\',z\' \\right )$时，可以得到p点满足如下等式：

$$x=r*\\cos\\alpha \\\\ y=r*\\sin\\alpha$$
同理， $p\'$也满足如下等式：
$$x\'=r*\\cos(\\alpha+\\beta )=r*(cos\\alpha\\cdot cos\\beta - \\sin \\alpha \\cdot \\sin \\beta )\\\\ y\'=r*\\sin(\\alpha+\\beta )=r*(\\sin \\alpha \\cdot \\cos \\beta +\\cos \\alpha \\cdot \\sin \\beta )$$

根据$p$和$p\'$的坐标等式，可以得到$p\'$的新的坐标表示：

$$x\'=x\\cos \\beta -y\\sin \\beta \\\\ y\'=x\\sin \\beta + y\\cos \\beta \\\\ z\'=z$$

有了以上旋转后的点的坐标公式，我们便可以编写顶点着色器代码了：

// 顶点着色器代码(决定顶点的位置、大小、颜色)
var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\\n' +
  'uniform float u_CosB, u_SinB;\\n' +
  'void main() \\n' +
     'gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;\\n' +
     'gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;\\n' +
     'gl_Position.z = a_Position.z;\\n' +
     'gl_Position.w = 1.0;\\n' +
     'gl_PointSize = 10.0;\\n' +      // 设置顶点的大小
  '\\n';

注意，我们可以通过 . 符号来访问一个vec4变量的x、y、z、w 四个分量值 ，绕着Z轴旋转，只需要计算x和y坐标值即可。

对于u_CosB和u_SinB，由于对三角形三个顶点而言，旋转的角度是一样的，所以变量应该是所有顶点共享，使用uniform进行声明，其赋值如下：

// 旋转的角度
var ANGLE = 30;
var radian = Math.PI * ANGLE / 180.0; //转为弧度
var cosB = Math.cos(radian);
var sinB = Math.sin(radian);

var u_CosB = context.getUniformLocation(context.program, 'u_CosB');
var u_SinB = context.getUniformLocation(context.program, 'u_SinB');
context.uniform1f(u_CosB, cosB);
context.uniform1f(u_SinB, sinB);

这段代码很简单，相信都应该明白了。

绕着Z轴逆序旋转30度的效果图：

如果想要的是顺时针的旋转，把ANGLE设置为负数即可，大家可以拿源码改改试试，这就是三角函数的精妙之处。

以上推导的是绕着Z轴进行旋转，其实绕着x轴或者y轴也可以用类似的方式进行推导，大家有兴趣可以试着推导一下。

缩放

缩放其实是比较简单的，我们来看缩放示意图：

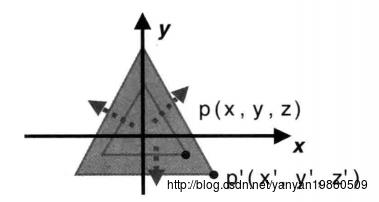
点$p(x,y,z)$ 缩放后，在三个轴的缩放因子为：$S_x$、$S_y$、$S_z$，则缩放后，点$p\'(x\',y\',z\')$的坐标如下：

$$x\'=x*S_x\\\\ y\'=y*S_y\\\\ z\'=z*S_z$$

然后我们来看下顶点着色器的代码：

// 顶点着色器代码(决定顶点的位置、大小、颜色)
var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\\n' +
  'uniform float a_Scale;\\n' +
  'void main() \\n' +
  '  gl_Position.x = a_Position.x * a_Scale;\\n' + 
  '  gl_Position.y = a_Position.y * a_Scale;\\n' + 
  '  gl_Position.z = a_Position.z * a_Scale;\\n' + 
  '  gl_Position.w = 1.0;\\n' + 
  '  gl_PointSize = 10.0;\\n' +      // 设置顶点的大小
  '\\n';

我们定义了一个uniform变量a_Scale，所有顶点都使用相同的缩放，然后对顶点的x、y、z值分别进行坐标变换。a_Scale的初始化也非常的简单。

// 三角形顶点的缩放
var scale = 0.5;
var u_Scale = context.getUniformLocation(context.program, 'a_Scale');
context.uniform1f(u_Scale, scale);

缩放后的三角形效果图：

小结

三角形的基础变换是非常重要的知识，还是要花点时间理解一下，目前使用的是简单的数学知识进行推导，其实，在图形学中，真正强大的是用矩阵进行计算，后面将会详细解说。

源码

点击下载(基本图形变换)

参考

<<WebGL编程指南>>