GDKOI2016Day1T1-魔卡少女拆位线段树维护区间内所有连续子区间的异或和

Posted 2020-08-17 Konjak谷弱

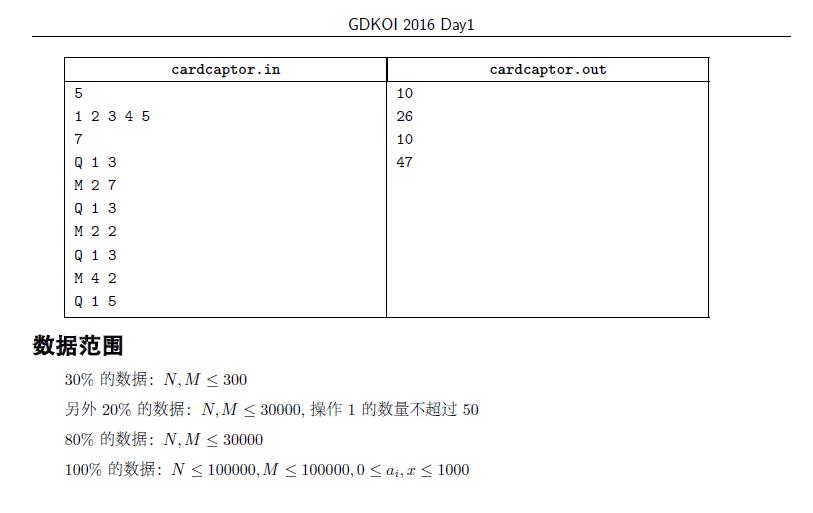
题意：给出N个数，M个操作。操作有修改和询问两种，每次修改将一个数改成另一个数，每次询问一个区间的所有连续子区间的异或和。n,m<=100000,ai<=1000

题解：

 

当年（其实也就是今年）做不出来的题。。D1T1啊。。。

因为ai<=1000，我们可以拆位处理。拆成10个二进制位，每位开1棵线段树。

对于每个节点，维护：

d：这段区间的异或和

L[0]，L[1]：子区间一定从左端点开始，异或和为0，1的子区间分别有多少个

R[0]，R[1]：子区间一定从右端点开始，异或和为0，1的子区间分别有多少个

s[0]，s[1]:异或和为0，1的子区间分别有多少个

然后重点就是合并啦。

 1 node upd(int ind,int tmp,node lc,node rc)
 2 {
 3     int dl=lc.d,dr=rc.d;
 4     node x;
 5     if(tmp!=0) x=t[ind][tmp];
 6     x.d=lc.d^rc.d;
 7     x.L[0]=(lc.L[0]+rc.L[(dl==0) ? 0:1])%mod;
 8     x.L[1]=(lc.L[1]+rc.L[(dl==0) ? 1:0])%mod;
 9     x.R[0]=(rc.R[0]+lc.R[(dr==0) ? 0:1])%mod;
10     x.R[1]=(rc.R[1]+lc.R[(dr==0) ? 1:0])%mod;
11     x.s[0]=(lc.s[0]+rc.s[0]+(lc.R[0]*rc.L[0])%mod+(lc.R[1]*rc.L[1])%mod)%mod;
12     x.s[1]=(lc.s[1]+rc.s[1]+(lc.R[0]*rc.L[1])%mod+(lc.R[1]*rc.L[0])%mod)%mod;
13     return x;
14 }

我打成node形式。。因为最后查询的时候有多个区间也要合并。。

 

代码：

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<iostream>
  6 #include<algorithm>
  7 using namespace std;
  8 
  9 typedef long long LL;
 10 const int N=100010;
 11 const LL mod=100000007;
 12 struct node{
 13     int l,r,lc,rc,d;
 14     LL L[2],R[2],s[2];
 15     //L:从左开始
 16     //R:从右开始
 17     //s:总答案
 18 }t[10][2*N];
 19 char c[10];
 20 int n,m,tl,a[N][10];
 21 LL bit[15];
 22 
 23 node upd(int ind,int tmp,node lc,node rc)
 24 {
 25     int dl=lc.d,dr=rc.d;
 26     node x;
 27     if(tmp!=0) x=t[ind][tmp];
 28     x.d=lc.d^rc.d;
 29     x.L[0]=(lc.L[0]+rc.L[(dl==0) ? 0:1])%mod;
 30     x.L[1]=(lc.L[1]+rc.L[(dl==0) ? 1:0])%mod;
 31     x.R[0]=(rc.R[0]+lc.R[(dr==0) ? 0:1])%mod;
 32     x.R[1]=(rc.R[1]+lc.R[(dr==0) ? 1:0])%mod;
 33     x.s[0]=(lc.s[0]+rc.s[0]+(lc.R[0]*rc.L[0])%mod+(lc.R[1]*rc.L[1])%mod)%mod;
 34     x.s[1]=(lc.s[1]+rc.s[1]+(lc.R[0]*rc.L[1])%mod+(lc.R[1]*rc.L[0])%mod)%mod;
 35     return x;
 36 }
 37 
 38 int bt(int ind,int l,int r)
 39 {
 40     int x=++tl;
 41     t[ind][x].l=l;t[ind][x].r=r;
 42     t[ind][x].lc=t[ind][x].rc=0;
 43     t[ind][x].d=0;
 44     memset(t[ind][x].L,0,sizeof(t[ind][x].L));
 45     memset(t[ind][x].R,0,sizeof(t[ind][x].R));
 46     memset(t[ind][x].s,0,sizeof(t[ind][x].s));
 47     if(l<r)
 48     {
 49         int mid=(l+r)/2;
 50         t[ind][x].lc=bt(ind,l,mid);
 51         t[ind][x].rc=bt(ind,mid+1,r);
 52         int lc=t[ind][x].lc,rc=t[ind][x].rc;
 53         t[ind][x]=upd(ind,x,t[ind][lc],t[ind][rc]);
 54     }
 55     else 
 56     {
 57         int d=a[l][ind];
 58         t[ind][x].d=d;
 59         t[ind][x].L[d]=t[ind][x].R[d]=t[ind][x].s[d]=1;
 60     }
 61     return x;
 62 }
 63 
 64 void change(int ind,int x,int p,int d)
 65 {
 66     if(t[ind][x].l==t[ind][x].r) 
 67     {
 68         t[ind][x].d=d;
 69         t[ind][x].L[d]=t[ind][x].R[d]=t[ind][x].s[d]=1;
 70         t[ind][x].L[d^1]=t[ind][x].R[d^1]=t[ind][x].s[d^1]=0;
 71         return ;
 72     }
 73     int lc=t[ind][x].lc,rc=t[ind][x].rc,mid=(t[ind][x].l+t[ind][x].r)/2;
 74     if(p<=mid) change(ind,lc,p,d);
 75     else change(ind,rc,p,d);
 76     t[ind][x]=upd(ind,x,t[ind][lc],t[ind][rc]);
 77 }
 78 
 79 node query(int ind,int x,int l,int r)
 80 {
 81     if(t[ind][x].l==l && t[ind][x].r==r) return t[ind][x];
 82     int lc=t[ind][x].lc,rc=t[ind][x].rc,mid=(t[ind][x].l+t[ind][x].r)/2;
 83     if(r<=mid) return query(ind,lc,l,r);
 84     else if(l>mid) return query(ind,rc,l,r);
 85     else
 86     {
 87         node a0=query(ind,lc,l,mid);
 88         node a1=query(ind,rc,mid+1,r);
 89         return upd(0,0,a0,a1);
 90     }
 91 }
 92 
 93 void output(int ind,int x)
 94 {
 95     int lc=t[ind][x].lc,rc=t[ind][x].rc;
 96     printf("l=%d r=%d d=%d l0=%lld l1=%lld r0=%lld r1=%lld s0=%lld s1=%lld\\n",t[ind][x].l,t[ind][x].r,t[ind][x].d,t[ind][x].L[0],t[ind][x].L[1],t[ind][x].R[0],t[ind][x].R[1],t[ind][x].s[0],t[ind][x].s[1]);
 97     if(lc) output(ind,lc);
 98     if(rc) output(ind,rc);
 99 }
100 
101 int main()
102 {
103     freopen("a.in","r",stdin);
104     freopen("me.out","w",stdout);
105     // freopen("cardcaptor.in","r",stdin);
106     // freopen("cardcaptor.out","w",stdout);
107     scanf("%d",&n);
108     int x,ind;node now;
109     bit[0]=1;
110     for(int i=1;i<=10;i++) bit[i]=bit[i-1]*2;
111     memset(a,0,sizeof(a));
112     for(int i=1;i<=n;i++) 
113     {
114         scanf("%d",&x);
115         ind=0;
116         while(x)
117         {
118             a[i][ind]=x%2;
119             x/=2;
120             ind++;
121         }
122     }
123     scanf("%d",&m);
124     for(int i=0;i<10;i++) {tl=0;bt(i,1,n);}
125     for(int i=1;i<=m;i++)
126     {
127         scanf("%s",c);
128         if(c[0]==\'Q\')
129         {
130             int l,r;LL ans=0;
131             scanf("%d%d",&l,&r);
132             for(int j=0;j<10;j++) 
133             {
134                 now=query(j,1,l,r);
135                 ans=(ans+(bit[j]*now.s[1])%mod)%mod;
136             }
137             printf("%lld\\n",ans);
138         }
139         else
140         {
141             int ind=0,p,d;
142             scanf("%d%d",&p,&d);
143             while(d)
144             {
145                 change(ind,1,p,d%2);
146                 d/=2;
147                 ind++;
148             }
149             for(int j=ind;j<10;j++) change(j,1,p,0);
150         }
151     }
152     return 0;
153 }