[拆位线段树]RMQ
Posted 鱼竿钓鱼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[拆位线段树]RMQ相关的知识,希望对你有一定的参考价值。
[拆位线段树]RMQ
题目
https://ac.nowcoder.com/acm/problem/21414
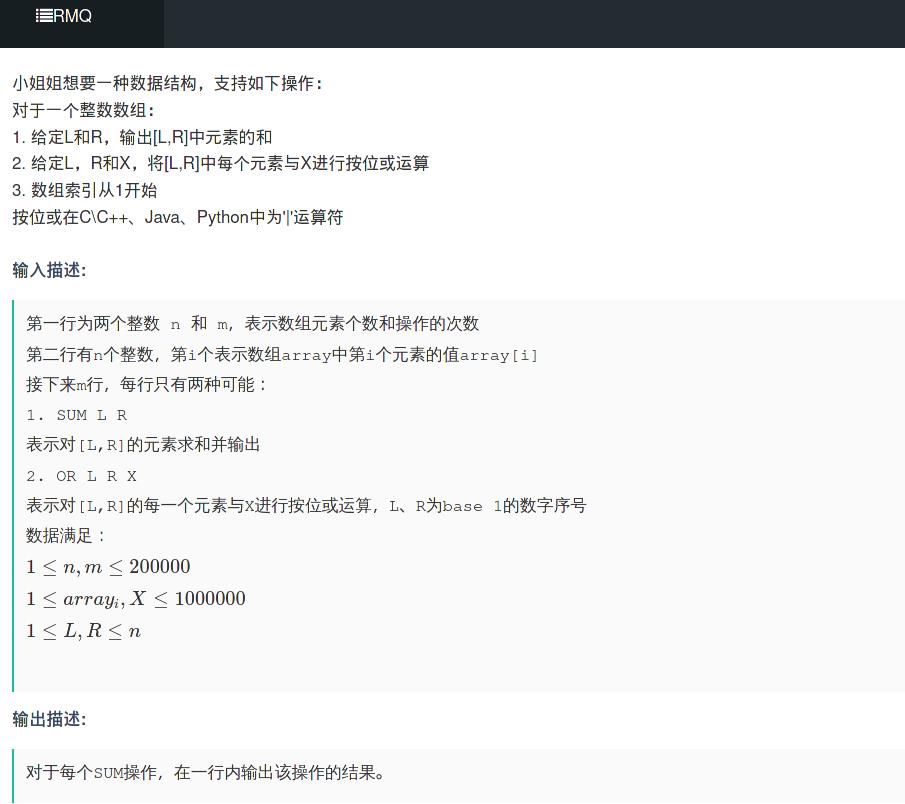
思路
区间或,区间求和
对于区间或,异或这种位运算,没法之间打懒标记。但是如果我们按位拆分,可以发现对于原数组都为01的线段树来说,或运算等效于区间设1。那么我们对每一位进行区间设1,区间求和操作,然后再最终求解答案的时候带上位权即可
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN=2e5+10;
int A[MAXN];
bool A_bit[MAXN][25];
struct tnode
{
bool lazy[25];
LL sum[25];
int l, r;
};
struct Segment_Tree
{
tnode t[4 * MAXN];
void init_lazy(int root,int i){
t[root].lazy[i]=0;
}
void union_lazy(int fa, int ch,int i){
t[ch].lazy[i]|=t[fa].lazy[i];
}
void cal_lazy(int root,int i){
t[root].sum[i]=(t[root].r-t[root].l+1);
return;
}
void push_down(int root,int i)
{
if (t[root].lazy[i])
{
cal_lazy(root,i);
if (t[root].l != t[root].r)
{
int ch = root << 1;
union_lazy(root, ch,i);
union_lazy(root, ch + 1,i);
}
init_lazy(root,i);
}
}
void update (int root,int i)
{
int ch = root << 1;
push_down(ch,i);
push_down(ch + 1,i);
t[root].sum[i]=t[ch].sum[i]+t[ch+1].sum[i];
}
void build(int root, int l, int r,int i)
{
t[root].l = l;t[root].r = r;
init_lazy(root,i);
if (l != r)
{
int mid = (l + r) >> 1;
int ch = root << 1;
build(ch, l, mid,i);
build(ch + 1, mid + 1, r,i);
update(root,i);
}
else{
t[root].sum[i]=A_bit[l][i];
}
}
void change(int root, int l, int r,int i)
{
push_down(root,i);
if (l == t[root].l && r == t[root].r)
{
t[root].lazy[i] = 1;
return;
}
int mid = (t[root].l + t[root].r) >> 1;
int ch = root << 1;
if (r <= mid)change(ch, l, r, i);
else if (l > mid)change(ch + 1, l, r, i);
else {change(ch, l, mid, i); change(ch + 1, mid + 1, r,i);}
update(root,i);
}
LL sum(int root, int l, int r, int i)
{
push_down(root,i);
if (t[root].l == l && t[root].r == r){
return t[root].sum[i];
}
int mid = (t[root].l + t[root].r) >> 1;
int ch = root << 1;
if (r <= mid)return sum(ch, l, r, i);
else if (l > mid)return sum(ch + 1, l, r, i);
else return sum(ch, l, mid, i) + sum(ch + 1, mid + 1, r, i);
}
};
Segment_Tree ST;
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&A[i]);
for(int i=1;i<=n;i++){
int j=0;
while(A[i]){
if(A[i]&1)A_bit[i][j++]=1;
else A_bit[i][j++]=0;
A[i]>>=1;
}
}
for(int i=0;i<=20;i++)ST.build(1, 1, n, i);
while(m--){
string op;cin>>op;
if(op=="SUM"){
int l,r;scanf("%d%d",&l,&r);
LL ans=0;
for(int i=0;i<=20;i++)ans+=(1LL<<i)*ST.sum(1,l,r,i);
printf("%lld\\n",ans);
}
else{
int l,r,x;scanf("%d%d%d",&l,&r,&x);
int i=0;
while(x){
if(x&1)ST.change(1,l,r,i);
x>>=1,i++;
}
}
}
return 0;
}
以上是关于[拆位线段树]RMQ的主要内容,如果未能解决你的问题,请参考以下文章