取快递的数学问题：手机尾号的重复概率

Posted 2020-08-15 假如你是李华

学校门口，四位手机尾号取快递。问：设有 \\(n\\) 个包裹，则存在两个包裹号码（收件人手机尾号，假设均匀分布）相同的概率 \\(P(n)\\) 是多少？

答曰：手机尾号一共有 \\(10^4=10000\\) 个，所以 \\( P(n)=\\frac{A_{10000}^n}{(10000)^n} \\), 其中 \\(A_n^r\\) 为排列数。

求出表达式非常简单，然而计算具体值时却遇到了麻烦：分子和分母都太大了，IEEE 754 浮点数受不了了，直接扔给我个 Infinity.

怎么办呢？把排列数展开，取对数，乘除变加减：

\\( \\log{P(n)} \\)

\\( = \\log{\\frac{A_{10000}^n}{(10000)^n}} \\)

\\( =\\log{A_{10000}^n}-n\\log{10^4} \\)

\\( =\\log{10^4(10^4-1)\\cdots(10^4-n+1)}-4n\\log{10} \\)

\\( =\\log{10^4}+\\log{(10^4-1)}+\\cdots+\\log{(10^4-n+1)}-4n\\log{10} \\)

不想这么麻烦的话，也有很精确的阶乘近似公式可用（这里就不限于整数了）：

\\( \\left\\{\\begin{matrix} n! = \\Gamma(n+1) \\\\ \\ln\\Gamma(z) \\approx \\tfrac{1}{2} \\left[\\ln(2\\pi) - \\ln z\\right] + z\\left[\\ln\\left(z + \\frac{1}{12z - \\frac{1}{10z}}\\right) - 1\\right] \\end{matrix}\\right. \\)

总之，最后能算出来具体的数。下面列出 n 取某些特殊值时的概率：

n	20	40	60	80	100	120	140	160	180	200
P(n)	2%	8%	16%	27%	39%	51%	62%	72%	80%	87%

\\([20, 200]\\) 区间内 \\(y=P(x)\\) 的函数图像如下（只有 \\(x\\) 等于整数的点有实际意义）：

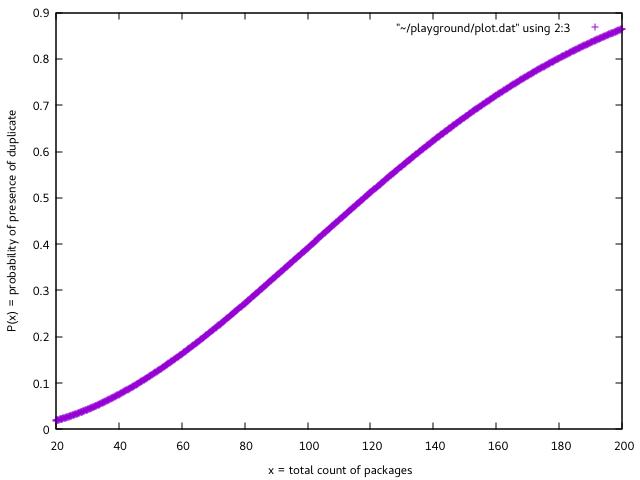
看起来有点反直觉：重复的概率怎么这么大？确实这么大，只要手机尾号是均匀分布的。

不过，自己的号跟某个人的号一样（存在某个人跟自己同号）的概率并不大：

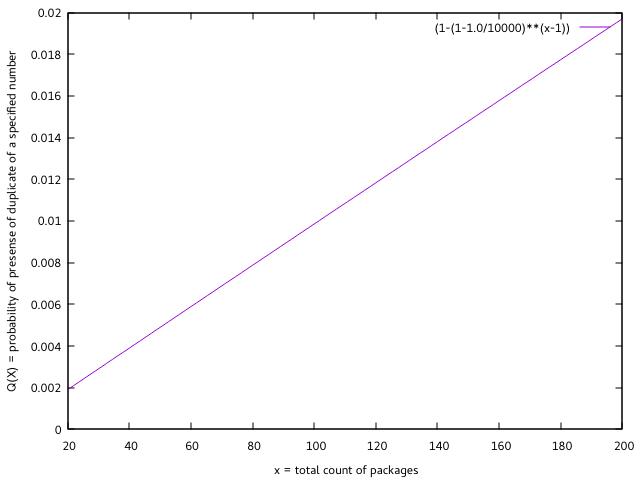
所以，重号的概率不小，但自己碰上的概率就很小了。（不过那大得吓人的重号概率还是很反直觉……）