BZOJ1061: [Noi2008]志愿者招募

Posted 2020-08-09 Bloodline

1061: [Noi2008]志愿者招募

Time Limit: 20 Sec  Memory Limit: 162 MB
Submit: 3752  Solved: 2298
[Submit][Status][Discuss]

Description

 

　　申奥成功后，布布经过不懈努力，终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难

题：为即将启动的奥运新项目招募一批短期志愿者。经过估算，这个项目需要N 天才能完成，其中第i 天至少需要

Ai 个人。 布布通过了解得知，一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天，招募费用

是每人Ci 元。新官上任三把火，为了出色地完成自己的工作，布布希望用尽量少的费用招募足够的志愿者，但这

并不是他的特长！于是布布找到了你，希望你帮他设计一种最优的招募方案。

Input

　　第一行包含两个整数N, M，表示完成项目的天数和可以招募的志愿者的种类。 接下来的一行中包含N 个非负

整数，表示每天至少需要的志愿者人数。 接下来的M 行中每行包含三个整数Si, Ti, Ci，含义如上文所述。为了

方便起见，我们可以认为每类志愿者的数量都是无限多的。

Output

　　仅包含一个整数，表示你所设计的最优方案的总费用。

Sample Input

3 3
2 3 4
1 2 2
2 3 5
3 3 2

Sample Output

14

HINT

 

1 ≤ N ≤ 1000，1 ≤ M ≤ 10000，题目中其他所涉及的数据均 不超过2^31-1。

 

神题....看了波题解才看懂https://www.byvoid.com/zhs/blog/noi-2008-employee/

#include<bits/stdc++.h>
#define rep(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
const int N=102333,inf=214748364;
struct Edge{
    int to,next,from,c,w;
}e[2000000];
int head[N],tot=1,ans,dis[N],from[N],x[N],m,n,a,T,b,c;
bool used[N];
inline void ins(int u,int v,int w,int cost) {
     e[++tot].to=v; e[tot].next=head[u]; head[u]=tot; e[tot].w=w; e[tot].c=cost; e[tot].from=u;
}

inline bool spfa() {
     queue<int> q; for(int i=0;i<=T;i++) dis[i]=inf; dis[0]=0; q.push(0); used[0]=1;  
     while(!q.empty()) {
          int x=q.front(); q.pop();
          for(int k=head[x];k;k=e[k].next) 
           if(e[k].w>0&&dis[x]+e[k].c<dis[e[k].to]){
                  dis[e[k].to]=dis[x]+e[k].c; from[e[k].to]=k;
                  if(!used[e[k].to]) {
                        used[e[k].to]=1; q.push(e[k].to);
                  }
            }
           used[x]=0;
     }
     if(dis[T]==inf) return 0;else return 1;
}

inline void run(){
     int x=inf;
     for(int k=from[T];k;k=from[e[k].from]) x=min(x,e[k].w);
     for(int k=from[T];k;k=from[e[k].from]) {
          e[k].w-=x; e[k^1].w+=x; ans+=e[k].c*x;
     }
}
inline void insert(int u,int v,int w,int c){
    ins(u,v,w,c); ins(v,u,0,-c);
}
int main(){
    scanf("%d%d",&n,&m);
    rep(i,1,n) scanf("%d",&x[i]);
    T=n+2;
    rep(i,2,n+1) insert(i,i-1,inf,0);
    rep(i,1,m) {
        scanf("%d%d%d",&a,&b,&c);
        insert(a,b+1,inf,c);
    }
    rep(i,1,n+1) {
        if(x[i]-x[i-1]<0) insert(i,T,x[i-1]-x[i],0);else insert(0,i,x[i]-x[i-1],0);
    }
    while(spfa()) run();
    printf("%d\n",ans);
}

View Code

这道题正确的解法是构造网络，求网络最小费用最大流，但是模型隐藏得较深，不易想到。构造网络是该题的关键，以下面一个例子说明构图的方法和解释。

例如一共需要4天，四天需要的人数依次是4,2,5,3。有5类志愿者，如下表所示：

种类	1	2	3	4	5
时间	1-2	1-1	2-3	3-3	3-4
费用	3	4	3	5	6

设雇佣第i类志愿者的人数为X[i]，每个志愿者的费用为V[i]，第j天雇佣的人数为P[j]，则每天的雇佣人数应满足一个不等式，如上表所述，可以列出

P[1] = X[1] + X[2] >= 4

P[2] = X[1] + X[3] >= 2

P[3] = X[3] + X[4] +X[5] >= 5

P[4] = X[5] >= 3

对于第i个不等式，添加辅助变量Y[i] (Y[i]>=0) ，可以使其变为等式

P[1] = X[1] + X[2] - Y[1] = 4

P[2] = X[1] + X[3] - Y[2] = 2

P[3] = X[3] + X[4] +X[5] - Y[3] = 5

P[4] = X[5] - Y[4] = 3

在上述四个等式上下添加P[0]=0,P[5]=0，每次用下边的式子减去上边的式子，得出

① P[1] - P[0] = X[1] + X[2] - Y[1] = 4

② P[2] - P[1] = X[3] - X[2] -Y[2] +Y[1] = -2

③ P[3] - P[2] = X[4] + X[5] - X[1] - Y[3] + Y[2] =3

④ P[4] - P[3] = - X[3] - X[4] + Y[3] - Y[4] = -2

⑤ P[5] - P[4] = - X[5] + Y[4] = -3

观察发现，每个变量都在两个式子中出现了，而且一次为正，一次为负。所有等式右边和为0。接下来，根据上面五个等式构图。

• 每个等式为图中一个顶点，添加源点S和汇点T。

• 如果一个等式右边为非负整数c，从源点S向该等式对应的顶点连接一条容量为c，权值为0的有向边；如果一个等式右边为负整数c，从该等式对应的顶点向汇点T连接一条容量为c，权值为0的有向边。

• 如果一个变量X[i]在第j个等式中出现为X[i]，在第k个等式中出现为-X[i]，从顶点j向顶点k连接一条容量为∞，权值为V[i]的有向边。

• 如果一个变量Y[i]在第j个等式中出现为Y[i]，在第k个等式中出现为-Y[i]，从顶点j向顶点k连接一条容量为∞，权值为0的有向边。

构图以后，求从源点S到汇点T的最小费用最大流，费用值就是结果。

根据上面的例子可以构造出如下网络，红色的边为每个变量X代表的边，蓝色的边为每个变量Y代表的边，边的容量和权值标已经标出(蓝色没有标记，因为都是容量∞，权值0)。

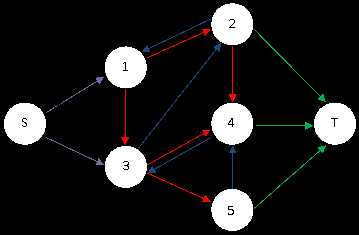
在这个图中求最小费用最大流，流量网络如下图，每个红色边的流量就是对应的变量X的值。

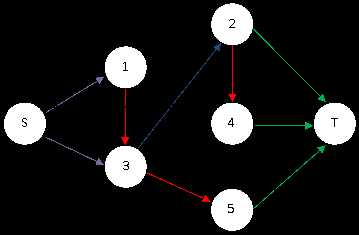
所以，答案为43+23+3*6=36。

上面的方法很神奇得求出了结果，思考为什么这样构图。我们将最后的五个等式进一步变形，得出以下结果

① - X[1] - X[2] + Y[1] + 4 = 0

② - X[3] + X[2] + Y[2] - Y[1] - 2 = 0

③ - X[4] - X[5] + X[1] + Y[3] - Y[2] + 3 = 0

④ X[3] + X[4] - Y[3] + Y[4] - 2 = 0

⑤ X[5] - Y[4] - 3 = 0

可以发现，每个等式左边都是几个变量和一个常数相加减，右边都为0，恰好就像网络流中除了源点和汇点的顶点都满足流量平衡。每个正的变量相当于流入该顶点的流量，负的变量相当于流出该顶点的流量，而正常数可以看作来自附加源点的流量，负的常数是流向附加汇点的流量。因此可以据此构造网络，求出从附加源到附加汇的网络最大流，即可满足所有等式。而我们还要求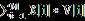最小，所以要在X变量相对应的边上加上权值，然后求最小费用最大流。