51nod - 1388 六边形平面

Posted 2020-08-09

题目链接：1388 六边形平面

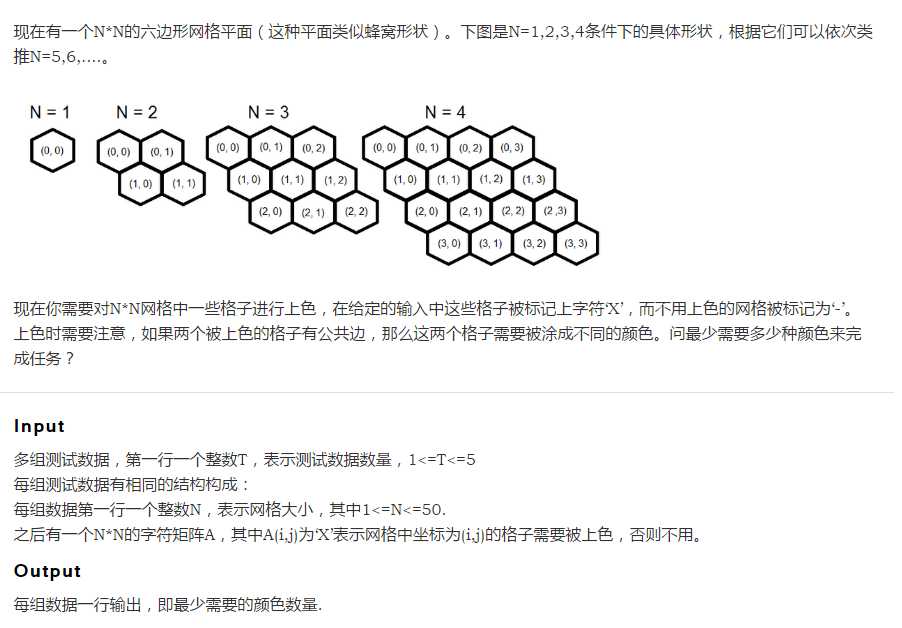
思路：乍一看，这不是挺简单的吗？判断有没有三个紧贴在一起的，或者两个贴在一起的。然后信心满满敲完了，交了，WA了。还好51nod可以下载数据，一看数据，哇！原来还有环！！然后再dfs跑过去看看有没有奇数环就好了。终于AC了！

 

 

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const int maxn = 50 + 5;
 5 char s[maxn][maxn];
 6 int n;
 7 int dx[] = {0, 0, 1, 1};
 8 int dy[] = {1, 0, 0, -1};
 9 bool valid(int x, int y) {
10     return x>=0&&y>=0&&x<n&&y<n;
11 }
12 int ety(int x, int y) {
13     return x*n+y;
14 }
15 int vis[maxn*maxn];
16 bool OK;
17 int tx[] = {0, -1, -1, 0, 1, 1};
18 int ty[] = {1, 1, 0, -1, -1, 0};
19 void dfs(int v, int u, int deep) {
20     if(vis[v]) {
21         if((deep - vis[v])&1) OK = true;
22         return ;
23     }
24     //printf("v : %d\n", v);
25     bool repeat = false;
26     //ans1 ++;
27     vis[v] = deep;
28     int x = v / n, y = v % n;
29     for(int i=0; i<6; i++) {
30         if(valid(x+tx[i], y+ty[i]) == false || s[x+tx[i]][y+ty[i]] != ‘X‘) continue;
31         if(repeat == false && ety(x+tx[i], y+ty[i]) == u) {
32             repeat = true; continue;
33         }
34         dfs(ety(x+tx[i], y+ty[i]), v, deep+1);
35     }
36 }
37 int main() {
38     freopen("in.txt", "r", stdin);
39     freopen("out.txt", "w", stdout);
40     int T;
41     scanf("%d", &T);
42     while(T--) {
43         memset(vis, 0, sizeof(vis));
44         scanf("%d", &n);
45         getchar();
46         int ans = 0;
47         for(int i=0; i<n; i++) {
48             gets(s[i]);
49         }
50         OK = false;
51         for(int i=0; i<n; i++) {
52             for(int j=0; j<n; j++) {
53                 if(vis[ety(i, j)] == 0 && s[i][j] == ‘X‘) dfs(ety(i, j), -1, 1);
54                 int t = 0;
55                 for(int k=0; k<3; k++) {
56                     if(valid(i+dx[k], j+dy[k]) && s[i+dx[k]][j+dy[k]] == ‘X‘) t ++;
57                 }
58                 ans = max(ans, t);
59                 t = 0;
60                 for(int k=1; k<4; k++) {
61                     if(valid(i+dx[k], j+dy[k]) && s[i+dx[k]][j+dy[k]] == ‘X‘) t ++;
62                 }
63                 ans = max(ans, t);
64             }
65         }
66         if(ans != 2) printf("%d\n", ans);
67         else {
68             printf("%d\n", ans+OK);
69         }
70     }
71     return 0;
72 }