51nod 1206 && hdu 1828 Picture (扫描线+离散化+线段树 矩阵周长并）

Posted 2020-11-10 Dysania_l

1206 Picture 

题目来源： IOI 1998

基准时间限制：2 秒 空间限制：131072 KB 分值: 160 难度：6级算法题

 收藏

 关注

给出平面上的N个矩形（矩形的边平行于X轴和Y轴），求这些矩形组成的所有多边形的周长之和。

 

 

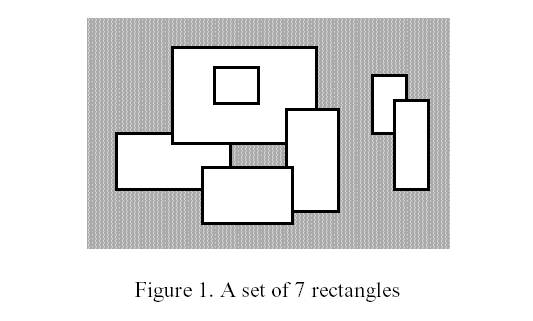
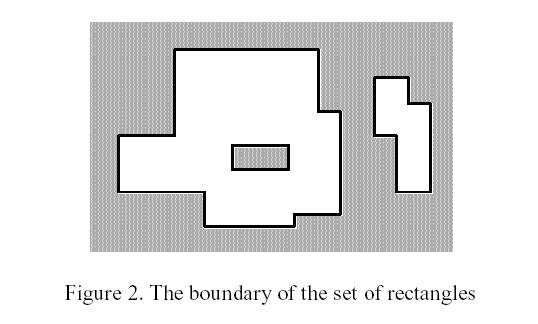
例如:N = 7。（矩形会有重叠的地方）。

 

合并后的多边形：

 

 

多边形的周长包括里面未覆盖部分方块的周长。

Input

第1行：1个数N。(2 <= N <= 50000)
第2 - N + 1行，每行4个数，中间用空格分隔，分别表示矩形左下和右上端点的坐标。（-1000000 <= X[i], Y[i] <= 1000000)

Output

输出多边形的周长。

Input示例

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Output示例

228

思路：
矩阵周长并模板题，hdu1828不需要离散化。。51nod上数据范围变大了需要离散化处理，写法和矩阵面积并差不多，多加了几个数组维护。

#include<bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mid int m = (l + r) >> 1
const int M = 1e5+10;
int cnt[M<<2];  //表示这个区间被重复覆盖了几次
int len[M<<2];   // 这个区间被覆盖的长度
int lp[M<<2],rp[M<<2]; //标记量，表示这个节点左右两个端点没有被覆盖，有则为1，无为0
int num[M<<2];  //这个区间被多少线段覆盖
int x[M<<2];
struct node{
    int h,l,r;
    int s;
    node(){}
    node(int a,int b,int c,int d):l(a),r(b),h(c),s(d){}
    bool operator < (const node &cmp) const {
        if(h == cmp.h) return s > cmp.s;
        return h < cmp.h;
    }
}t[M<<2];

void pushup(int l,int r,int rt){
    if(cnt[rt]){
        lp[rt] = rp[rt] = 1;
        num[rt] = 2;
        len[rt] = x[r+1] - x[l];
    }
    else if(l == r){
        num[rt] = len[rt] = lp[rt] = rp[rt] = 0;
    }
    else{
        lp[rt] = lp[rt<<1];
        rp[rt] = rp[rt<<1|1];
        len[rt] = len[rt<<1] + len[rt<<1|1];
        num[rt] = num[rt<<1] + num[rt<<1|1];
        if(lp[rt<<1|1]&&rp[rt<<1]) num[rt] -= 2; // 左右两边两条线重合，变成一条线段
    }
}

void update(int L,int R,int c,int l,int r,int rt){
    if(L <= l&&R >= r){
        cnt[rt] += c;
        pushup(l,r,rt);
        return;
    }
    mid;
    if(L <= m) update(L,R,c,lson);
    if(R > m) update(L,R,c,rson);
    pushup(l,r,rt);
}

int main()
{
    int n;
    while(cin>>n){
    int m = 0;
    while(n--){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        x[m] = a;
        t[m++] = node(a,c,b,1);
        x[m] = c;
        t[m++] = node(a,c,d,-1);
    }
    int k = 1;
    sort(x,x+m); sort(t,t+m);
    for(int i = 1;i < m;i ++){
        if(x[i] != x[i-1]) x[k++] = x[i];
    }
    memset(cnt,0,sizeof(cnt));
    memset(num,0,sizeof(num));
    int ret = 0,last = 0;
    for(int i = 0;i < m;i ++){
        int l = lower_bound(x,x+k,t[i].l)-x;
        int r = lower_bound(x,x+k,t[i].r)-x-1;
        if(l <= r) update(l,r,t[i].s,0,k-1,1);
        ret += num[1]*(t[i+1].h - t[i].h);
        ret += abs(len[1] - last);
        last = len[1];
    }
    cout<<ret<<endl;
    }
    return 0;
}