NOIP2011pj表达式的值[树形DP 笛卡尔树]

Posted 2020-08-07 Candy?

题目描述

对于1 位二进制变量定义两种运算：

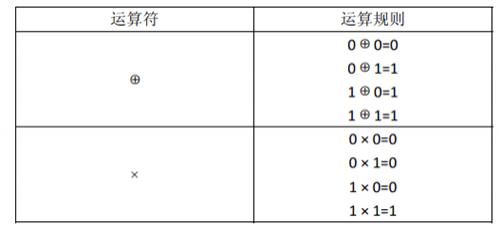
运算的优先级是：

1. 先计算括号内的，再计算括号外的。

2. “× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如+(*_)，请你在横线处填入数字0 或者1 ，请问有多少种填法可以使得表达式的值为0 。

输入输出格式

输入格式：

输入文件名为exp.in ，共 2 行。

第1 行为一个整数 L，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 L 个字符，其中只包含’（’、’）’、’+’、’*’这4 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号 

输出格式：

输出文件exp.out 共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对10007 取模后的结果。

输入输出样例

输入样例#1：

4
+(*)

输出样例#1：

３

说明

【输入输出样例说明】

  给定的表达式包括横线字符之后为：+(*_) 

  在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。 

【数据范围】

对于20% 的数据有 0 ≤ L ≤ 10。

对于50% 的数据有 0 ≤ L ≤ 1,000。

对于70% 的数据有 0 ≤ L ≤ 10,000 。

对于100%的数据有 0 ≤ L ≤ 100,000。

对于50% 的数据输入表达式中不含括号。

－－－－－－－－－－－－－－－－－－－－－－－－－

一开始想了一个区间DP的做法f[i][j][0/1]表示i到j为0或1的方案数，内存爆的连编译都不编译

然后想到建表达式树 树形DP，白书上的方法只能拿80分

然后找到了这篇文章http://wenku.baidu.com/link?url=jvyUVTTGFC27LnlHkzQ0OObqeBFDwCYvuCbiHHG5CaPXrjFiGoBtiLhdfNIhW1vHNNZ-Umb_zTKnCOQK3WTw0N8KRQT8m2lfBBMsHpoIChC

 

用 笛卡尔树 建表达式树

百科

有点像treap，key按左右分，value按上下分

表达式树中key就是顺序，本来就按照这个顺序；value是算术优先级，设括号个数为p，‘+‘:p*2+1  ‘*‘:p*2+2，value小的在上面

笛卡尔树有O(n)的建树方法：

可以发现key本来有序，新加的元素只能在当前的右链上，有可能吧本来右链上一些元素转到左子树上

用一个stack维护右链上的元素就好了，每次找第一个<=当前的

//
//  main.cpp
//  表达式的值树形dp
//
//  Created by Candy on 9/6/16.
//  Copyright ? 2016 Candy. All rights reserved.
//


#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N=100005,MOD=10007;
int n;
char s[N];
struct node{
    int ls,rs;
    char op;
}tree[N*16];
int cnt=0,w[N],root=0;
void build(){
    int p=0,cnt=0;
    for(int i=1;i<=n;i++){
        if(s[i]==‘(‘) p++;if(s[i]==‘)‘) p--;
        if(s[i]==‘+‘) {w[++cnt]=p*2+1;
            tree[cnt].op=s[i];
        }
        if(s[i]==‘*‘) w[++cnt]=p*2+2,tree[cnt].op=s[i];;
    }
    
    int st[N],k,top=-1;
    for (int i=1;i<=cnt;i++)
    {
        k = top;
        while (k >= 0 && w[st[k]] > w[i]) k--;
        if(k!=-1) tree[st[k]].rs=i;
        if (k < top) tree[i].ls=st[k+1];
        st[++k] = i;
        top=k;
    }
    root=st[0];
}
int f[N][2];
void dp(int i){//printf("dp %d\n",i);
    if(i==0) return;
    if(f[i][0]!=0) return;
    int ls=tree[i].ls,rs=tree[i].rs;char op=tree[i].op;
    dp(ls);dp(rs);
    if(op==‘+‘){
        f[i][0]=f[ls][0]*f[rs][0];
        f[i][1]=f[ls][0]*f[rs][1]+f[ls][1]*f[rs][0]+f[ls][1]*f[rs][1];
    }
    if(op==‘*‘){
        f[i][1]=f[ls][1]*f[rs][1];
        f[i][0]=f[ls][0]*f[rs][1]+f[ls][1]*f[rs][0]+f[ls][0]*f[rs][0];
    }
    f[i][1]%=MOD;f[i][0]%=MOD;
}
int main(int argc, const char * argv[]) {
    scanf("%d%s",&n,s+1);
    build();
    f[0][0]=f[0][1]=1;
    dp(root);
    printf("%d",f[root][0]%MOD);
    return 0;
}

 

当然也可以用stack做，一个操作符栈一个数据栈，数据栈中是0/1的方案数

一开始push一个empty，以后每次一个+ *都push一个empty

//from 题解
//Candy?修改

#include<cstdio>
#include<cstring>
const int mod=10007;
struct node{
    int a,b;
}f[100010];
const node emp=(node){1,1};
char s[100010];
char st[100010];int n,tp=0,fp=0;

void cal(char op,node &a,node &b){
    if(op==‘+‘) a.b=(a.b*(b.a+b.b)+a.a*b.b)%mod,a.a=a.a*b.a%mod;
    else a.a=(a.a*(b.a+b.b)+a.b*b.a)%mod,a.b=a.b*b.b%mod;
}

int main(){
    scanf("%d%s",&n,s);
    st[++tp]=‘(‘; f[++fp]=emp;
    s[n++]=‘)‘;
    for(int i=0;i<n;i++){
        if(s[i]==‘(‘)st[++tp]=‘(‘;
        else if(s[i]==‘)‘){
            for(;st[tp]!=‘(‘;tp--,fp--)
                cal(st[tp],f[fp-1],f[fp]);//pop 2 push 1
            tp--;// (
        }
        else{
            for(;st[tp]<=s[i]&&st[tp]!=‘(‘;tp--,fp--)// ‘*‘ < ‘+‘
                cal(st[tp],f[fp-1],f[fp]);
            st[++tp]=s[i],f[++fp]=emp;//every +/* with a number
        }
    }
    return!printf("%d\n",f[1].a%mod);
}