主题模型TopicModel:隐含狄利克雷分布LDA
Posted -柚子皮-
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了主题模型TopicModel:隐含狄利克雷分布LDA相关的知识,希望对你有一定的参考价值。
http://blog.csdn.net/pipisorry/article/details/42649657
主题模型LDA简介
隐含狄利克雷分布简称LDA(Latent Dirichlet allocation),首先由Blei, David M.、吴恩达和Jordan, Michael I于2003年提出,目前在文本挖掘领域包括文本主题识别、文本分类以及文本相似度计算方面都有应用。
LDA是一种典型的词袋模型,即它认为一篇文档是由一组词构成的一个集合,词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
它是一种主题模型,它可以将文档集中每篇文档的主题按照概率分布的形式给出;
同时是一种无监督学习算法,在训练时不需要手工标注的训练集,需要的仅仅是文档集以及指定主题的数量k即可;
此外LDA的另一个优点则是,对于每一个主题均可找出一些词语来描述它;
LDA可以被认为是一种聚类算法:
- 主题对应聚类中心,文档对应数据集中的例子。
- 主题和文档在特征空间中都存在,且特征向量是词频向量。
- LDA不是用传统的距离来衡量一个类簇,它使用的是基于文本文档生成的统计模型的函数。
LDA的概率图及生成表示
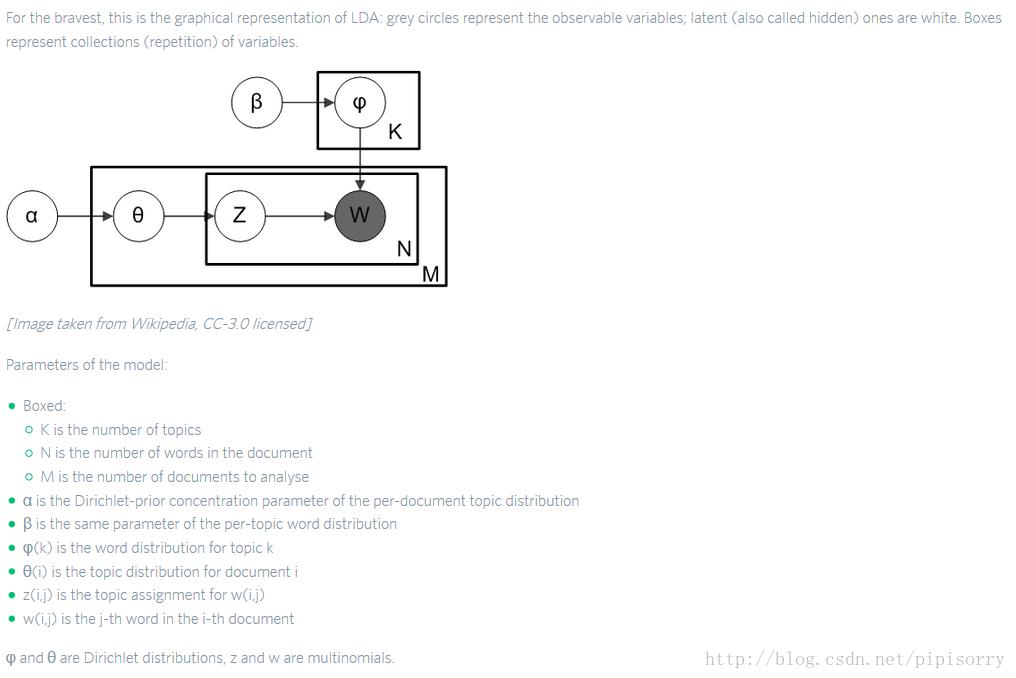

[LDA automatically assigns topics to text documents]
Note:
1 阴影圆圈表示可观测的变量,非阴影圆圈表示隐变量;箭头表示两变量间的条件依赖性;方框表示重复抽样,方框右下角的数字代表重复抽样的次数。这种表示方法也叫做plate notation,参考PRML 8.0 Graphical Models。
对应到图2, α⃗ 和 β⃗ 是超参数;方框中, Φ={φ⃗ k} 表示有 K 种“主题-词项”分布; Θ={ϑ⃗ m} 有 M 种“文档-主题”分布,即对每篇文档都会产生一个 ϑ⃗ m 分布;每篇文档 m 中有 n 个词,每个词 wm,n 都有一个主题 zm,n ,该词实际是由 φ⃗ zm,n 产生。
2 β⃗ 到φ(生成topic-word分布的分布) and α⃗到θ(生成doc-topic分布的分布) 是狄利克雷分布,θ生成z(赋给词w的主题) and φ生成w(当前词) 是多项式分布。θ指向z是从doc-topic分布中采样一个主题赋给w(但是此时还不知道词w具体是什么,而是只知道其主题),φ指向w是φ的topic-word分布依赖于w。
LDA生成模型
当我们看到一篇文章后,往往喜欢推测这篇文章是如何生成的,我们可能会认为作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文。LDA就是要根据给定的一篇文档,推测其主题分布。
因此正如LDA贝叶斯网络结构中所描述的,在LDA模型中一篇文档生成的方式如下:
- 从狄利克雷分布
 中取样生成文档i的主题分布
中取样生成文档i的主题分布
- 从主题的多项式分布
 中取样生成文档i第j个词的主题
中取样生成文档i第j个词的主题
- 从狄利克雷分布
 中取样生成主题
中取样生成主题 的词语分布
的词语分布
- 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语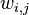
LDA模型参数求解概述
因此整个模型中所有可见变量以及隐藏变量的联合分布是
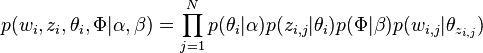 (这里i表示第i个文档)
(这里i表示第i个文档)
最终一篇文档的单词分布的最大似然估计可以通过将上式的 以及
以及 进行积分和对
进行积分和对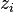 进行求和得到
进行求和得到
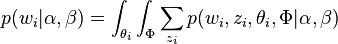
根据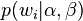 的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
LDA的参数估计(吉布斯采样)
在LDA最初提出的时候,人们使用EM算法进行求解。
后来人们普遍开始使用较为简单的Gibbs Sampling,具体过程如下:
- 首先对所有文档中的所有词遍历一遍,为其都随机分配一个主题,即zm,n=k~Mult(1/K),其中m表示第m篇文档,n表示文档中的第n个词,k表示主题,K表示主题的总数,之后将对应的n(k)m+1, nm+1, n(t)k+1, nk+1, 他们分别表示在m文档中k主题出现的次数,m文档中主题数量的和??(可重复的,所以应该就是文档中词的个数,不变的量)??,k主题对应的t词的次数,k主题对应的总词数(n(k)m等等初始化为0)。
- 之后对下述操作进行重复迭代。
- 对所有文档中的所有词进行遍历,假如当前文档m的词t对应主题为k,则n(k)m-1, nm-1, n(t)k-1, nk-1, 即先拿出当前词,之后根据LDA中topic sample的概率分布采样出新主题,在对应的n(k)m, nm, n(t)k, nk上分别+1。
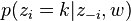 ∝
∝ 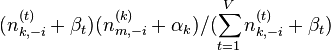 (topic sample的概率分布)
(topic sample的概率分布)
- 迭代完成后输出主题-词参数矩阵φ和文档-主题矩阵θ
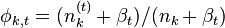 主题k中词t的概率分布
主题k中词t的概率分布
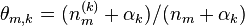 文档m中主题k的概率分布
文档m中主题k的概率分布
从这里看出,gibbs采样方法求解lda最重要的是条件概率p(zi | z-i,w)的计算上。
[http://zh.wikipedia.org/wiki/隐含狄利克雷分布]
LDA中的数学基础
- beta分布是二项式分布的共轭先验概率分布:“对于非负实数
 和
和 ,我们有如下关系
,我们有如下关系
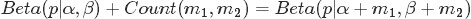
以上是关于主题模型TopicModel:隐含狄利克雷分布LDA的主要内容,如果未能解决你的问题,请参考以下文章