折半搜索

Posted 2023-01-03 sjsjsj-minus-si

折半搜索 （meet in the middle）

/*
reference:
    
translation:
    
solution:

trigger:
    
note:
    *
date:
    2019.09.04
*/
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define dwn(i,a,b) for(int i=a;i>=b;--i) 
template <typename T> inline void rd(T &x)x=0;char c=getchar();int f=0;while(!isdigit(c))f|=c=='-';c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48);c=getchar();x=f?-x:x; 
#define mem(a,b) memset(a,b,sizeof(a))
#define ee(i,x) for(int i=head[x];i;i=e[i].next)

int n,t;
int sum,tmp;
int a[50];

bool found=false;
map<int,bool> mp;

inline void dfs1(int h,int t)
    if(h>t)
        mp[tmp]=1;
        return ;
    
    dfs1(h+1,t);
    tmp+=a[h];
    dfs1(h+1,t);
    tmp-=a[h];


inline void dfs2(int h,int t)
    if(h>t)
        if(mp[sum-tmp])found=1;
        return ;
    
    dfs2(h+1,t);
    tmp+=a[h];
    dfs2(h+1,t);
    tmp-=a[h];


#undef int
int main()
#define int long long
    rd(n),rd(sum);
    rep(i,1,n)rd(a[i]);
    dfs1(1,n/2);
    dfs2(n/2+1,n);
    printf(found?"YES":"NO");
    return 0;

/*
5 67
34 546 5 35 32
*/

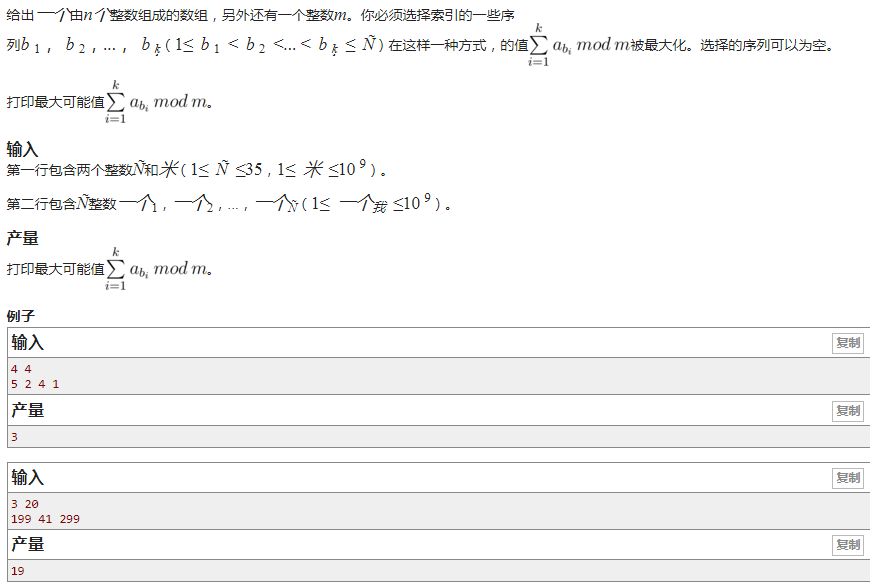
CF888E Maximum_Subsequence

/*
reference:
    
translation:
    
solution:
    考虑到dfs的效率很低很低而且mod数在1e9的范围，肯定要用一个stl的容器啊（set）
    2的35次方会超时，考虑折半搜索，前后分别枚举，最后二分取最大值即可。
trigger:
    
note:
    *
date:
    2019.09.04
*/
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define dwn(i,a,b) for(int i=a;i>=b;--i) 
template <typename T> inline void rd(T &x)x=0;char c=getchar();int f=0;while(!isdigit(c))f|=c=='-';c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48);c=getchar();x=f?-x:x; 
#define mem(a,b) memset(a,b,sizeof(a))
#define ee(i,x) for(int i=head[x];i;i=e[i].next)

const int N = 40; 
int a[N],n,mod,ans;
set<int>s,t;

inline void dfs1(int cur,int sum)
    if(cur==n>>1|1)
        sum=sum%mod;
        s.insert(sum);
        return ;
    
    dfs1(cur+1,sum);
    dfs1(cur+1,sum+a[cur]);



inline void dfs2(int cur,int sum)
    if(cur==n+1)
        sum=sum%mod;
        t.insert(sum);
        return ;
    
    dfs2(cur+1,sum);
    dfs2(cur+1,sum+a[cur]);


#undef int
int main()
#define int long long
    rd(n),rd(mod);
    rep(i,1,n)
        rd(a[i]);
    
    dfs1(1,0);
    dfs2(n>>1|1,0);
    for(auto it=s.begin();it!=s.end();++it)
        int tmp=*it;
        auto pos=t.lower_bound(mod-tmp);
        if(pos!=t.end())
            --pos;
            if(*pos+tmp<=mod)
                ans=max(ans,*pos+tmp);
        
    
    printf("%lld",ans);
    return 0;

法2：two_pointers

/*
4 4 
5 2 4 1
*/
//3
/*
3 20 
199 41 299
*/
//19

/*
reference:
    
translation:
    
solution:
    法2：two_pointer 来找两个区间的在一定值的限定区间的最大值，如本题要求
    在x数组和y数组（要排个序）中各选择一个数的和<=mod-1，并使这个值最大
    很显然，快指针从前往后，慢指针倒序，如果当前值比mod-1大了那么j--，因为i再怎么往后移值都不可能
    <=mod-1，（因为是按照升序排序的） 
trigger:
    
note:
    *注意最大值<=mod-1而不是<=mod，你太瓜啦 
date:
    2019.09.04
*/
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define dwn(i,a,b) for(int i=a;i>=b;--i) 
template <typename T> inline void rd(T &x)x=0;char c=getchar();int f=0;while(!isdigit(c))f|=c=='-';c=getchar();while(isdigit(c))x=(x<<1)+(x<<3)+(c^48);c=getchar();x=f?-x:x; 
#define mem(a,b) memset(a,b,sizeof(a))
#define ee(i,x) for(int i=head[x];i;i=e[i].next)

const int N = 40; 
int a[N],x[N],y[N],n,mod,ans;
int tot1,tot2;
//set<int>s,t;

inline void dfs1(int cur,int sum)
    if(cur==n/2+1)
        sum=sum%mod;
        x[++tot1]=sum;
        //s.insert(sum);
        return ;
    
    dfs1(cur+1,sum);
    dfs1(cur+1,sum+a[cur]);



inline void dfs2(int cur,int sum)
    if(cur==n+1)
        sum=sum%mod;
        y[++tot2]=sum;
        //t.insert(sum);
        return ;
    
    dfs2(cur+1,sum);
    dfs2(cur+1,sum+a[cur]);


#undef int
int main()
#define int long long
    freopen("cf888e.txt","r",stdin);
    rd(n),rd(mod);
    rep(i,1,n)
        rd(a[i]);
    
    dfs1(1,0);
    dfs2(n>>1|1,0);
    /*for(auto it=s.begin();it!=s.end();++it)
        int tmp=*it;
        auto pos=t.lower_bound(mod-tmp);
        if(pos!=t.end())
            --pos;
            if(*pos+tmp<=mod)/////////////////这里应该是< 
                ans=max(ans,*pos+tmp);
        
    */
    sort(x+1,x+tot1+1);
    sort(y+1,y+tot2+1);
    /*rep(i,1,tot1)printf("%lld ",x[i]);
    puts("");
    rep(i,1,tot2)printf("%lld ",y[i]);
    puts("");*/ 
    for(int i=1,j=tot2;i<=tot1;++i)
        if(x[i]+y[j]>=ans && x[i]+y[j]<=mod-1)
            ans=x[i]+y[j];
        while(j && x[i]+y[j]<ans)
            j--;
    
    printf("%lld",ans);
    return 0;