tarjan缩点与割点
Posted chiarochinoful
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了tarjan缩点与割点相关的知识,希望对你有一定的参考价值。
Tarjan算法
先是废话时间:说来挺惭愧 , 好几个月以前就学过tarjan算法然而现在才第一次写
tarjan缩点&dp
为啥要缩点答案显然
把环缩成一个点
然后图上拓扑dp
tarjan同名算法有很多 , 比如本blog的缩点与割点的tarjan算法其实并不是一个东西 , 但是很是相似
这个tarjan , 需要三个东西
第一:一个栈来存放搜到的点
第二:一个时间戳dfn , 表示第几个搜到这个点的
第三:low数组 , 表示够追溯到的最早的栈中节点的次序号
首先 , 初始化的时候肯定有
1 dfn[now] = low[now] = ++Index
然后开始遍历边
如果遍历到的点没有碰过
那么递归tarjan
递归结束后
1 low[now] = std::min(low[now], low[to]);
那么如果下一个点已经去过了呐
那么就不用递归了
1 low[now] = std::min(low[now], dfn[to]);
为什么是dfn呢?
照我的理解 , 应该是如果直接用low说不定会跳到这个环以外的地方
不过这个缩点tarjan里面把dfn换成low是可以的 , 但是一会的割点tarjan就不可以了
当最后时一个点的low == dfn , 那个这个点注定是一个缩点之后仍然存留在图上的一个点
那么就可以快落缩点了 , 把栈里的元素不停的向外弹就是了
然后根据题目性质拓扑dp , 没了
1 #include<cmath> 2 #include<queue> 3 #include<stack> 4 #include<cstdio> 5 #include<cstring> 6 #include<cstdlib> 7 #include<iostream> 8 #include<algorithm> 9 #define APART puts("----------------------") 10 #define debug 1 11 #define FILETEST 0 12 #define inf 100010 13 #define ll long long 14 #define ha 998244353 15 #define INF 0x7fffffff 16 #define INF_T 9223372036854775807 17 #define DEBUG printf("%s %d\\n",__FUNCTION__,__LINE__) 18 19 namespace chino 20 21 inline void setting() 22 #if FILETEST 23 freopen("test.in", "r", stdin); 24 freopen("test.me.out", "w", stdout); 25 #endif 26 return; 27 28 29 inline int read() 30 char c = getchar(), up = c; int num = 0; 31 for(; c < ‘0‘ || c > ‘9‘; up = c, c = getchar()); 32 for(; c >= ‘0‘ && c <= ‘9‘; num = (num << 3) + (num << 1) + (c ^ ‘0‘), c = getchar()); 33 return up == ‘-‘ ? -num : num; 34 35 36 int n, m; 37 int ans; 38 int cntE, cntR, cntJ; 39 int val[inf], dp[inf]; 40 int vis[inf], in[inf]; 41 int belong[inf], dfn[inf], low[inf]; 42 int head[inf], rehead[inf]; 43 struct Edge 44 int to; 45 int from; 46 int next; 47 e[inf << 1], r[inf << 1]; 48 std::queue <int> Q; 49 std::stack <int> S; 50 51 inline void AddEdge(int from, int to, int &cntE, int *head, Edge *e) 52 ++cntE; 53 e[cntE].from = from; 54 e[cntE].to = to; 55 e[cntE].next = head[from]; 56 head[from] = cntE; 57 return; 58 59 60 void tarjan(int now) 61 low[now] = dfn[now] = ++cntJ; 62 vis[now] = 1; 63 S.push(now); 64 for(int i = head[now]; i; i = e[i].next) 65 int to = e[i].to; 66 if(dfn[to] == 0) 67 tarjan(to); 68 low[now] = std::min(low[now], low[to]); 69 else if(vis[to]) 70 low[now] = std::min(low[now], dfn[to]); 71 72 if(low[now] == dfn[now]) 73 int top = S.top(); 74 while(1) 75 top = S.top(); 76 S.pop(); 77 belong[top] = now; 78 vis[top] = 0; 79 if(top == now) 80 break; 81 val[now] += val[top]; 82 83 84 return; 85 86 87 inline void topoDP() 88 while(!Q.empty()) 89 Q.pop(); 90 for(int i = 1; i <= n; i++) 91 if(belong[i] == i && in[i] == 0) 92 Q.push(i), dp[i] = val[i]; 93 94 while(!Q.empty()) 95 int x = Q.front(); 96 Q.pop(); 97 for(int i = rehead[x]; i; i = r[i].next) 98 int to = r[i].to; 99 dp[to] = std::max(dp[to], dp[x] + val[to]); 100 --in[to]; 101 if(in[to] == 0) 102 Q.push(to); 103 104 105 return; 106 107 108 inline int main() 109 n = read(); 110 m = read(); 111 for(int i = 1; i <= n; i++) 112 val[i] = read(); 113 for(int i = 1; i <= m; i++) 114 int u = read(); 115 int v = read(); 116 AddEdge(u, v, cntE, head, e); 117 118 for(int i = 1; i <= n; i++) 119 if(dfn[i] == 0) 120 tarjan(i); 121 122 for(int i = 1; i <= m; i++) 123 int u = belong[e[i].from]; 124 int v = belong[e[i].to]; 125 if(u == v) 126 continue; 127 AddEdge(u, v, cntR, rehead, r); 128 ++in[v]; 129 130 topoDP(); 131 for(int i = 1; i <= n; i++) 132 ans = std::max(ans, dp[i]); 133 printf("%d\\n", ans); 134 return 0; 135 136 137 //namespace chino 138 139 int main()return chino::main();
复杂度O(n+m)
下一题:P3388 【模板】割点(割顶)
说在前面 , 这道题是无向边 , 上一题是有向边
而割点的定义是:
在无向连通图中,如果将其中一个点以及所有连接该点的边去掉,图就不再连通,那么这个点就叫做割点(cut vertex / articulation point)。
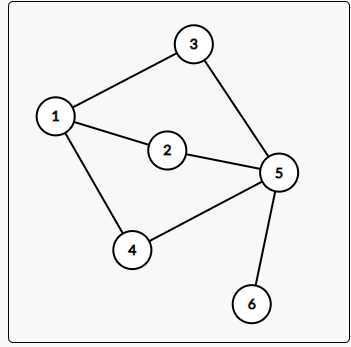
举例 , 这张图5点就是割点
求割点, 也是一个叫做tarjan的算法
首先
以上是关于tarjan缩点与割点的主要内容,如果未能解决你的问题,请参考以下文章