图的割点与割边

Posted 2021-01-05 lyfoi

割点

什么是割点？

如果在一个图中，如果把一个点删除，那么这个图不再联通，那么这个点就是割点（割顶），当然是在无向图。

如何实现？

如果我们尝试删除每个点，并且判断这个图的联通性，那么复杂度会特别的高。所以要介绍一个常用的算法：(Tarjan)。

首先，我们上一个图：

很容易的看出割点是 ２，而且这个图仅有这一个割点。

首先，我们按照 (DFS) 序给他打上时间戳（访问的顺序）。

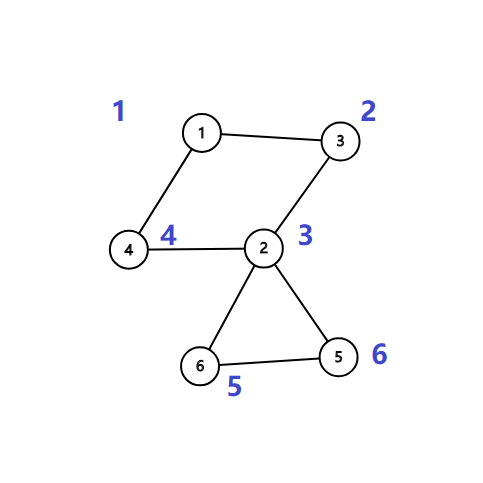
这些信息被我们保存在一个叫做 num 的数组中。

还需要另外一个数组 low，用它来存储不经过其父亲（你有多个那么就看你遍历到了哪个）能到达的时间戳。

例如 ２ 的话是 １， ５ 和 ６ 是 ３。

然后我们开始 (DFS)，我们判断某个点是否是割点的根据是：对于某个顶点 (u)，如果存在至少一个顶点 (v) （ (u) 的儿子），使得 (low_v>=num_u)，即不能回到祖先，那么 (u) 点为割点。

另外，如果搜到了自己（在环中），如果他有两个及以上的儿子，那么他一定是割点了，如果只有一个儿子，那么把它删掉，不会有任何的影响。比如下面这个图，此处形成了一个环，从树上来讲它有 ２ 个儿子：

我们在访问 １ 的儿子时候，假设先 (DFS) 到了 ２，然后标记用过，然后递归往下，来到了 ４， ４ 又来到了 ３，当递归回溯的时候，会发现 ３ 已经被访问过了，所以不是割点。

更新 low 的伪代码如下：

如果 v 是 u 的儿子
    low[u]=min(low[u],low[v]);
否则
    low[u] = min(low[u],num[v]);

洛谷 P3388 【模板】割点（割顶）

Code

/*
洛谷 P3388 【模板】割点（割顶）
算法： Tarjan
时间：2018 8 22
by @liyifeng 
*/
#include<bits/stdc++.h>
using namespace std;
int n,m;//n：点数 m：边数 
int num[100001],low[100001],inde,res;
//num：记录每个点的时间戳 low：能不经过父亲到达最小的编号，inde：时间戳，res：答案数量 
bool vis[100001],flag[100001];//flag: 答案 vis：标记是否重复 
vector <int> edge[100001];// 存图用的 
void Tarjan(int u,int father)//u 当前点的编号，father 自己爸爸的编号 
{
    vis[u]=true;// 标记 
    low[u]=num[u]=++inde;// 打上时间戳 
    int child=0;// 每一个点儿子数量 
    for(auto v : edge[u])// 访问这个点的所有邻居 （C++11） 
    {
        if(!vis[v])
        {
            child++;// 多了一个儿子 
            Tarjan(v,u);// 继续 
            low[u]=min(low[u],low[v]);// 更新能到的最小节点编号 
            if(father!=u&&low[v]>=num[u]&&!flag[u])// 主要代码 
            // 如果不是自己，且不通过父亲返回的最小点符合割点的要求，并且没有被标记过 
            // 要求即为：删了父亲连不上去了，即为最多连到父亲
            {
                flag[u]=true;
                res++;// 记录答案 
            }
        }
        else if(v!=father)
            low[u]=min(low[u],num[v]);// 如果这个点不是自己，更新能到的最小节点编号 
    }
    if(father==u&&child>=2&&!flag[u])// 主要代码，自己的话需要 2 个儿子才可以 
    {
        flag[u]=true;
        res++;// 记录答案 
    }
}
int main()
{
    cin>>n>>m;// 读入数据 
    for(int i=1;i<=m;i++)// 注意点是从 1 开始的 
    {
        int x,y;
        cin>>x>>y;
        edge[x].push_back(y);
        edge[y].push_back(x);
    }// 使用 vector 存图 
    for(int i=1;i<=n;i++)// 因为 Tarjan 图不一定联通 
        if(!vis[i])
        {
            inde=0;// 时间戳初始为 0 
            Tarjan(i,i);// 从第 i 个点开始，父亲为自己 
        }
    cout<<res<<endl;
    for(int i=1;i<=n;i++)
        if(flag[i]) cout<<i<<" ";// 输出结果 
    for(int i=1;i<=n;i++) cout<<low[i]<<endl;
    return 0;
}

割边

什么是割边？

和割点差不多，还叫做割桥。

无向联通图中，去掉一条边，图中的连通分量数增加，则这条边，称为桥或者割边，当然也是在无向图。

实现

和割点差不多，只要改一处： (low_v>num_u) 就可以了，而且不需要考虑根节点的问题。

割边是和是不是根节点没关系的，原来我们求割点的时候是指点 (v) 是不可能不经过父节点 (u) 为回到祖先节点（包括父节点），所以顶点 (u) 是割点。如果 (low_v==num_u) 表示还可以回到父节点，如果顶点 (v) 不能回到祖先也没有另外一条回到父亲的路，那么 (u-v) 这条边就是割边

(Tarjan) 算法还有许多用途，常用的例如求强连通分量，缩点，还有求 (2-SAT) 的用途等。