矩阵乘法

Posted 2022-10-06 mowanying

概念：

A是n*m的矩阵，B是m*p的矩阵，则A*B是n*p的矩阵。

这个矩阵的某一位置的值（i，j）是A中第 i 行的每一个数 * B中第 j 行的每一个数求和的值。

比如：（图片来源）

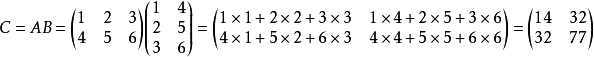
用途：

用于处理一维递推，递推次数很大的时候：构造一个转移矩阵，根据转移方程填充转移矩阵的值。然后根据结合律，可以做矩阵快速幂来加速。

模板：P1939 【模板】矩阵加速（数列）

#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
#define ll long long
void mul(int f[3],int a[3][3])//两两乘法 

    int tmp[3];
    memset(tmp,0,sizeof(tmp));
    for(int i=0;i<=2;i++)
     for(int k=0;k<=2;k++)
      tmp[i]=(tmp[i] + (ll) f[k]*a[k][i] %mod) %mod;//注意这里的下标 
    memcpy(f,tmp,sizeof(tmp));

void mulself(int a[3][3])//自己乘自己 

    int tmp[3][3];
    memset(tmp,0,sizeof(tmp));
    for(int i=0;i<=2;i++)
     for(int j=0;j<=2;j++)
      for(int k=0;k<=2;k++)
       tmp[i][j]=(tmp[i][j] + (ll)a[i][k]*a[k][j]%mod ) %mod;
    memcpy(a,tmp,sizeof(tmp));

int main()

    int T,n;
    scanf("%d",&T);
    while(T--)
        scanf("%d",&n);
        int f[3]=1,1,1;//初始状态数组 
        int a[3][3]=0,0,1,1,0,0,0,1,1;//转移数组 
        n--;//根据题意适当地-- 
        while(n)
            if(n&1) mul(f,a);
            mulself(a);
            n>>=1;
         
        printf("%d\\n",f[0]);
    
 
/*
3
6
8
10
*/

模板

P1962 斐波那契数列

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
void mul(int f[2],int a[2][2])

    int tmp[2];
    memset(tmp,0,sizeof(tmp));
    for(int i=0;i<=1;i++)
     for(int k=0;k<=1;k++)
         tmp[i]=( tmp[i]+(ll)f[k]*a[k][i] %mod ) %mod;//!!!k 这里是k 因为是行*列 
     
    memcpy(f,tmp,sizeof(tmp));

void mulself(int a[2][2])

    int tmp[2][2];
    memset(tmp,0,sizeof(tmp));//!!!一定要记得清零啊！！否则会是一些莫名其妙的值 
    for(int i=0;i<=1;i++)//注意下标是从0开始 
     for(int j=0;j<=1;j++)
      for(int k=0;k<=1;k++)
          tmp[i][j]=( tmp[i][j]+(ll)a[i][k]*a[k][j] %mod ) %mod;
      
    memcpy(a,tmp,sizeof(tmp));

int main()

    ll n;
    scanf("%lld",&n);
    int f[2]=0,1;
    int c[2][2]=0,1,1,1;
    while(n)
        if(n&1) mul(f,c);
        mulself(c);
        n>>=1;
    
    printf("%d\\n",f[0]);

斐波拉契

 

P4838 P哥破解密码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 19260817
void mul(int f[3],int a[3][3])

    int tmp[3];
    memset(tmp,0,sizeof(tmp));
    for(int i=0;i<=2;i++)
     for(int k=0;k<=2;k++)
         tmp[i]=(tmp[i] + (ll)f[k]*a[k][i] %mod) %mod;
     
    memcpy(f,tmp,sizeof(tmp));

void mulself(int a[3][3])

    int tmp[3][3];
    memset(tmp,0,sizeof(tmp));
    for(int i=0;i<=2;i++)
     for(int j=0;j<=2;j++)
         for(int k=0;k<=2;k++)
         tmp[i][j]=(tmp[i][j] + (ll)a[i][k]*a[k][j] %mod) %mod;
     
    
    memcpy(a,tmp,sizeof(tmp));

int main()

    int T,n;
    scanf("%d",&T);
    while(T--)
        scanf("%d",&n);
        int f[3]=1,1,0;
        int a[3][3]=1,1,0,1,0,1,1,0,0;
        n--;
        while(n)
            if(n&1) mul(f,a);
            mulself(a);
            n>>=1;
        
        printf("%d\\n",( (f[0]+f[1]) %mod + f[2] ) %mod  );//这个+mod写在外面啊！！！仔细一点检查！！！ 
    

/*
3
1
3
6
*/

P哥破解密码

注意：

1.记得清零

2.下标看清楚

3.mod不要写错位置