U65320 Oak的预算方案

Posted 2022-08-11 xiongchongwen

如有乱码，请点击。

题目背景

早在 ((-1)^2k(k\in N)-\dfrac1e^i\pi)((−1)2k(k∈N)−eiπ1?) 年前，

OakOak 便帮助 金明 解决了他的 预算方案 问题：

题目描述

金明 今天很开心，家里购置的新房就要领钥匙了，新房里有一间 金明 自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 NN 元钱就行”。今天一早， 金明 就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

|  主件   |         附件          |

|  电脑   | 打印机，扫描仪 |

|  书柜   |         图书          |

|  书桌   |    台灯，文具     |

| 工作椅 |          无            |

如果要买归类为附件的物品，必须先买该附件所属的主件。附件不再有从属于自己的附件。 金明 想买的东西很多，肯定会超过妈妈限定的 NN 元。于是，他把每件物品规定了一个重要度，分为 kk 等：用整数 1\sim k1∼k 表示，第 kk 等最重要。他还从因特网上查到了每件物品的价格。他希望在不超过 NN 元（可以等于 NN 元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 jj 件物品的价格为 v[j]v[j] ，重要度为 p[j]p[j] ，共选中了 kk 件物品，编号依次为 j_1,j_2,...,j_kj1?,j2?,...,jk? ，则所求的总和为：

v[j_1]\times p[j_1]+v[j_2]\times p[j_2]+...+v[j_k]\times p[j_k]v[j1?]×p[j1?]+v[j2?]×p[j2?]+...+v[jk?]×p[jk?]

---

现在 OakOak 不满足于解决这类简单的问题(因为他需要购置满满一大卡车的物品)，于是他请你帮忙设计一个程序帮他处理那数据规模庞大的物品清单。

输入格式

第11行，为两个正整数，用一个空格隔开：N\;mNm（其中NN表示总钱数，mm为希望购买物品的个数。）

从第22行到第m+1m+1行，第ii行给出了编号为i-1i−1的物品的基本数据，每行有33个非负整数 v_i-1\;p_i-1\;q_i-1vi−1?pi−1?qi−1?（其中v_i-1vi−1?表示该物品的价格，p_i-1pi−1?表示该物品的重要度，q_i-1qi−1?表示该物品是主件还是附件。如果 q_i-1=0qi−1?=0，表示该物品为主件，如果 q_i-1>0qi−1?>0，表示该物品为附件，q_i-1qi−1?是所属主件的编号）

输出格式

一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值。

输入输出样例

输入 #1复制

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

输出 #1复制

2200

输入 #2复制

10000 20
300 2 0
500 2 1
200 4 1
800 1 1
600 5 1
650 3 1
600 3 1
750 2 1
650 1 1
850 4 1
550 3 1
850 2 1
700 4 1
950 1 1
950 5 1
700 5 1
500 2 1
650 3 1
800 3 1
850 4 1

输出 #2复制

35200

说明/提示

数据范围：

---

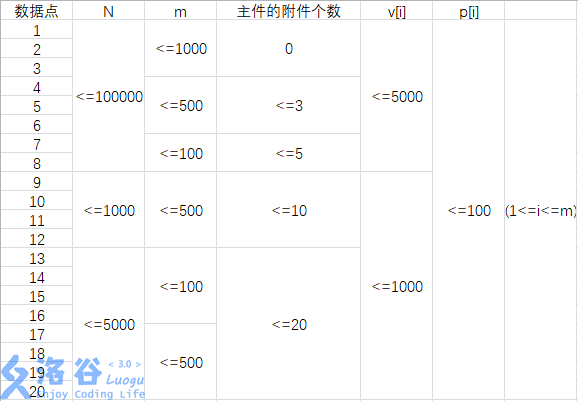
样例解释：

1：选择4,5号物品，此时所求总和为400×3+500×2=2200；

2：选择1,7∼20号物品，所求总和为35200。

---

提示：

请注意时间和空间限制。

可以使用O2?优化

 

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
int n,m;
int f[5000010],h[5000010];
struct node
    int v,p,q;
a[1010];
int read()
	int a=0,b=1;
	char ch=getchar();
	while((ch<48||ch>57)&&ch!=‘-‘)
		ch=getchar();
	
	if(ch==‘-‘)
		b=-1;
		ch=getchar();
	
	while(ch<48||ch>57)
		ch=getchar();
	
	while(ch>47&&ch<58)
		a=a*10+ch-48;
		ch=getchar();
	
	return a*b;

int main()
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    	a[i].v=read(),a[i].p=read(),a[i].q=read();
        a[i].p*=a[i].v;
    
    for(int i=1;i<=m;i++)
        if(!a[i].q)
            for(int j=1;j<a[i].v;j++)
                h[j]=0;
            
            for(int j=a[i].v;j<=n;j++)
                h[j]=f[j-a[i].v]+a[i].p;
            
            for(int j=1;j<=m;j++)
                if(a[j].q==i)
                    for(int k=n;k>=a[i].v+a[j].v;k--)
                        h[k]=max(h[k],h[k-a[j].v]+a[j].p);
                    
                
            
            for(int j=a[i].v;j<=n;j++)
                f[j]=max(f[j],h[j]);
            
        
    
    printf("%d",f[n]);
    return 0;