计算几何模板：多边形与凸包

Posted 2021-12-19 liguanlin1124

---恢复内容开始---

比较有意思的，旋（xuan）转（zhuan）卡（qia）壳（ke），还有半平面交都在这里。

---

 

1.多边形与凸包

左边是一个多边形，右边是一个凸包：

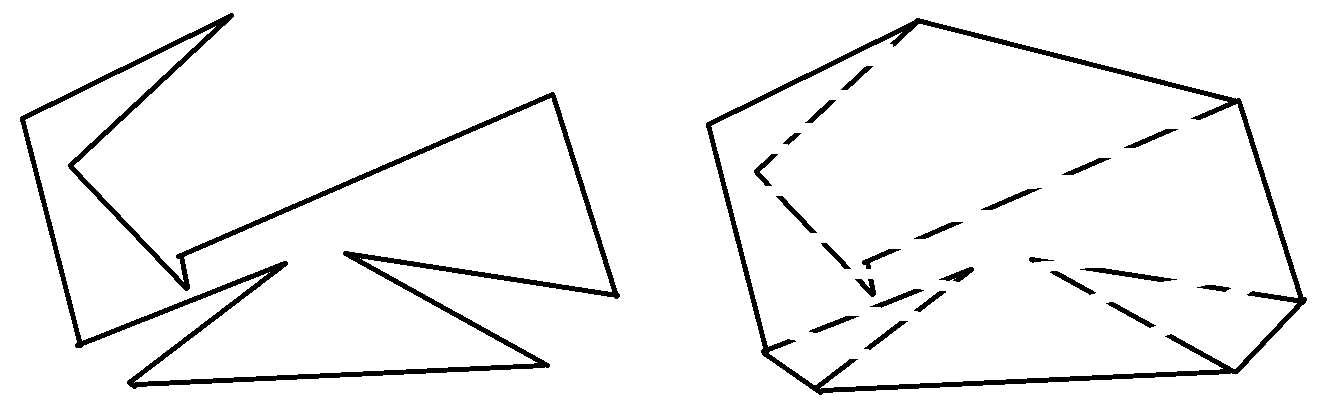
一般用按某一方向遍历整个多边形/凸包的数组/vector表示。

2.求凸包面积

随便找一个顶点，然后向不相邻的点连边，将凸包分成$(n-2)$个小三角形。

然后叉积就好了。

最后注意叉积求的是有向面积。（大力推荐逆时针遍历

typedef vector<Point> Pol;
double S_(Pol p)

    double ret = 0;
    for(int i=1,lim=(int)p.size();i<lim-1;i++)
        ret+=((p[i]-p[0])^(p[i+1]-p[0]));
    return ret/2;

求凸包面积

3.判断点是否在多边形内

有一个方法（射线法）：以该点为起点做一条射线，若穿过奇数次边界则点在多边形内。

实现的时候对于顶点的地方有个技巧。我们可以遵守左包含右不包含（虽然反过来也一样），这样对于一个顶点来说，要么算两次，要么一次不算，不会影响判定。

int P_in_Pol(Point p,Pol P)

    int now = 0,n = P.size();
    for(int i=0;i<n;i++)
    
        if(P_S(p,P[i],P[(i+1)%n]))return -1;
        int zt = dcmp((P[(i+1)%n]-P[i])^(p-P[i]));
        int d0 = dcmp(p.x-P[i].x);
        int d1 = dcmp(p.x-P[(i+1)%n].x);
        if(zt>0&&d0>=0&&d1<0)now^=1;
        if(zt<0&&d1>=0&&d0<0)now^=1;
    
    return now;

点在多边形内

4.建凸包

这里的建凸包不是在普通的斜率优化$dp$里的单建上/下凸包，是给出散点建一个整体凸包。

大体做法是，将点排序，先按$x$升序再按$y$升序。

然后按逆时针顺序建凸包。要保证的是，凸包上先后两条边的叉积是恒为正的，相当于一条向量逆时针转了一圈。

建完第一遍之后，我们得到的是下凸包，这时候再反着扫一遍，依然保证叉积恒为正即可。

int build(int n,Point *p,Point *s)

    sort(p,p+n);
    int m = 0;
    for(int i = 0;i < n;i++)
    
        while(m>1&&((s[m-1]-s[m-2])^(p[i]-s[m-2]))<=0)m--;
        s[++m] = p[i];
    
    int lim = m;
    for(int i = n-2;i >= 0;i--)
    
        while(m>lim&&((s[m-1]-s[m-2])^(p[i]-s[m-2]))<=0)m--;
        s[++m] = p[i];
    
    if(m!=1)m--;
    return m;

建凸包

5.直线切割凸包（返回直线左边的点）

比较暴力？

暴力扫，用叉积判断点是否在直线左边（或直线上）。如果直线与当前线段相交就把交点扔进去。

Pol Cut_Pol(Pol p,Line l)

    Pol ret;int n = p.size();
    for(int i=0;i<n;i++)
    
        Point p0 = p[i],p1 = p[(i+1)%n];
        if(dcmp(l.v^(p0-l.x))>=0)ret.push_back(p0);
        if(dcmp(l.v^(p1-p0)))
        
            Point tmp = L_L(l,Line(p0,p1-p0));
            if(P_S(tmp,p0,p1))ret.push_back(tmp);
        
    
    return ret;

一刀切凸包

6.半平面交

首先介绍一下他是干嘛的。

（当然不是我介绍）

用途？比如求一堆多边形重叠部分多大了长什么样子。

其实还是很暴力的。双端队列大力维护点集+边集，然后……

（我已经想好了一个绝佳的方式，可惜这里太小写不下）

主要见代码。

const int N = 1050;
Point tmpP[N];
Line tmpL[N];
bool Onleft(Line l,Point p)

    return dcmp((l.v^(p-l.x))) > 0;

int HalfPol(Line *l,int n,Pol &p)

    sort(l,l+n);
    int hd = 0,tl = 0;
    tmpL[0] = l[0];
    for(int i=0;i<n;i++)
    
        while(hd<tl&&!Onleft(l[i],tmpP[tl-1]))tl--;
        while(hd<tl&&!Onleft(l[i],tmpP[hd]))hd++;
        tmpL[++tl] = l[i];
        if(!dcmp(tmpL[tl].v^tmpL[tl-1].v))
        
            tl--;
            if(Onleft(tmpL[tl],l[i].x))tmpL[tl]=l[i];
        
        if(hd<tl)tmpP[tl-1] = L_L(tmpL[tl-1],tmpL[tl]);
    
    while(hd<tl&&!Onleft(tmpL[hd],tmpP[tl-1]))tl--;
    if(tl-hd<=1)return 0;
    tmpP[tl] = L_L(tmpL[hd],tmpL[tl]);
    int m = 0;
    for(int i=hd;i<=tl;i++)p.push_back(tmpP[i]);
    return m;

半平面交

7.旋转卡壳

求凸包直径怎么求？

想象有一对平行的夹子，一段夹在凸包的某条边上，另一端自己转，一直转到一个最舒服的位置就像这样：

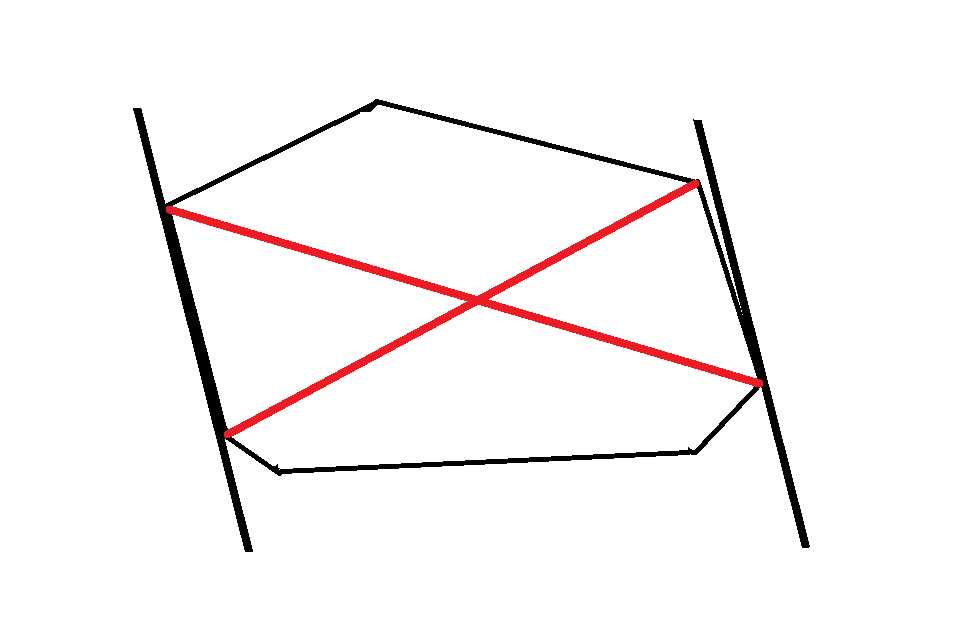
现在夹子之间最长的是两条红线长的$max$。

代码：

double rororokk(Pol p)

    int n = p.size();
    int i = 0,j = 1;p[n]=p[0];
    double ans = 0.0;
    for(;i<n;i++)
    
        while(j<n&&((p[j+1]-p[i+1])^(p[i]-p[i+1]))>((p[j]-p[i+1])^(p[i]-p[i+1])))j=(j+1)%n;
        ans = max(ans, max(lth(p[j]-p[i]),lth(p[j+1]-p[i+1])));
    
    return ans;

旋转卡壳