数据结构第六章学习小结--- 图

Posted 2021-12-01 liuzhhhao

在第十一和第十二周的学习中，我了解到了有关图的一些知识，图是一种比线性表和树更为复杂的数据结构，她不像线性表一样，数据元素之间具有线性关系，每个元素对应一个前驱和一个后继，她也不像树一样，数据元素之间有明显的层次关系，简而言之，在图结构中，结点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。感觉自己这一周有点松懈了，pta上面的题目都只是看一遍题目觉得不会就去翻书，或是求助同学，缺少独立思考！！！欸，还是先讲讲有关图的一些基本知识吧。

1、 图的定义

         图是由顶点的有穷非空集合和顶点之间边的集合组成，通过表示为G(V,E)，其中，G标示一个图，V是图G中顶点的集合，E是图G中边的集合。

         无边图：若顶点Vi到Vj之间的边没有方向，则称这条边为无项边（Edge），用序偶对(Vi,Vj)标示。

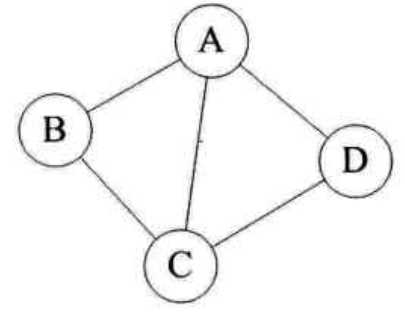
         对于下图无向图G1来说，G1=(V1, {E1})，其中顶点集合V1={A,B,C,D}；边集合E1={(A,B),(B,C),(C,D),(D,A),(A,C)}:

                                

         有向图：若从顶点Vi到Vj的边是有方向的，则成这条边为有向边，也称为弧（Arc）。用有序对（Vi，Vj）标示，Vi称为弧尾，Vj称为弧头。如果任意两条边之间都是有向的，则称该图为有向图。

         有向图G2中，G2=（V2,{E2}），顶点集合（A,B,C,D）,弧集合E2={<A,D>,{B,A},<C,A>,<B,C>}.

         权（Weight）：有些图的边和弧有相关的数，这个数叫做权（Weight）。这些带权的图通常称为网（Network）。

2、  图的存储结构

邻接矩阵：图的邻接矩阵存储方式是用两个数组来标示图。一个一位数组存储图顶点的信息，一个二维数组（称为邻接矩阵）存储图中边或者弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

图的邻接矩阵存储表示：

#define MaxInt 10000  //表示极大值，即∞
#define MVNum 100    //最大顶点数
typedef char VerTexType;//假设顶点的数据类型为字符型
typedef int ArcType;        //假设边的权值类型为整型
typedef struct
{
    VerTexType Vexs[MVNum]; //顶点表
    ArcType arcs[MVNum] [MVNum]; //邻接矩阵
    int vexnum,arcnum;           //图的当前点数和边数
}AMGraph;

 

邻接表：图的链式存储结构

#define MvNum 100       //最大顶点数 
typedef struct ArcNode    //边结点
{
    int adjvex;            //该边所指向的顶点的位置 
    struct ArcNode *nextarc;//指向下一条边的指针 
}ArcNode;

typedef struct VNode    //顶点信息
{
    VertexType data;
    ArcNode *firstarc;  //指向第一条依附该顶点的边的指针 
}VNode,AdjList[MvNum];  //AdjList表示邻接表类型

typedef struct
{
    AdjList Vertices;   //一维数组
    int vexnum,arcnum;  //图的当前顶点数和边数 
}Graph;

采用邻接表表示法创建无向图：

Void CreateUDG(ALGraph &G)
{/*采用邻接表表示法创建无向图G*/
 cin>>G.vexnum>>G.arcnum;/*输入总顶点数，总边数*/
for(i=0;i<G.vexnum;++i)
{
 cin>>G.vertices[i].data;/*顶点值*/
 G.vertices[i].firstarc=NULL;
}
for(k=0;k<G.arcnum;++k)
{/*输入各边，构造邻接表*/
cin>>v1>>v2;/*一条边对应的两个顶点*/
i=LocateVex(G,v1);
j=LocateVex(G,v2);/*确定v1,v2在G.vertices[i]的序号*/
p1=new ArcNode;
p1->adjvex=j;
p1->nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;
p2=new ArcNode;
p2->adjvex=i;
p2->nextarc=G.vertices[j].firstarc;
G.vertices[j].firstarc=p1
}
}

3、图的遍历

（1）深度优先搜索遍历

深度优先搜索遍历连通图是一个递归的过程（划重点？）

辅助数组：vi[i]--访问标志数组，赋初值为"false"(若已被访问，则将相应的分量置为true。

邻接矩阵表示的深度优先搜索遍历

void DFS(Graph a,int b) //深度优先搜索 
{
    visited[b]=true;    //令顶点对应的visited数组为true，表示该顶点已被访问过 
    cout<<b<<" ";   //输出顶点编号及空格 
     
    for(int i=0;i<a.vexnum;i++)
    {
        if(a.arcs[b][i]==1 && visited[i]==false)DFS(a,i);   //若顶点对应的邻接点未被访问，则递归调用DFS函数 
}
}

 

（2）广度优先搜索遍历

特点：尽可能先对横向进行搜索

辅助数组：visited[i]-访问标志数组！！！

void BFS(Graph a,int b) //广度优先搜索 
{
    int temp;   //定义参数 
     
    while(!q.empty())   //若队列不为空 
    {
        temp=q.front(); //取队头元素值为temp 
        q.pop();    //队头元素出队 
             
        cout<<temp<<" ";    //输出temp值及空格 
     
        for(int i=0;i<a.vexnum;i++)
        {
            if(a.arcs[temp][i]==1 && visited[i]==false) //若顶点对应的邻接点未被访问，则邻接点入队 
            {
                q.push(i);  //邻接点入队 
                visited[i]=true;    //邻接点对应的visited数组取true，表示已被访问 
            }
        }
    visited[b]=true;    //第一次入队的顶点对应的visited数组值取true，表示已被访问
    }
}

4、图的应用

（1）最小生成树--在一个连通的所有生成树之中，各边权值之和最小的那个生成树

a 普里姆算法（从名字上就能看出非常的高大上）又称为“加点法”（逐步增加U中的顶点）

辅助数组：clsoedge[i]--记录从U到U-V具有最小权值的边（lowcost+adjvex)

struct{
VerTexType adjvex;
ArcType lowcost;
}closedge[MVNUM];

b 克鲁斯卡尔算法---“加边法”（逐步增加生成树的边）

辅助数组：Edge[i]--储存边的信息

struct{

VerTexType Head;

VerTexType Tail;

ArcType lowcost;

}Edge[arcnum];

                 Vexset[i]--标识各个顶点所属的连通分量

int VexSet[MVNUM];

(2)最短路径--从源点到其余各顶点的最短路径

迪杰斯特拉算法（按照路径长短递增的次序产生最短路径）

 

目标的完成情况：

  这几周上课没能集中精力，没有及时复习上一章的内容，被上次的小测成绩打击到了，有点遗憾，平时打的练习题还不够多。这两周都有尽量去pta上答题，可是效率不高，遇到编程题就不会，没有思路，结果到现在还没完成。

接下来的目标：这几天深夜加班爆肝一下，尝试自己把题目弄懂，必要时多多借鉴同学的博客，看别人在遇到问题时是怎样解决的。

参考资料：大话数据结构-图论 https://www.cnblogs.com/w-wanglei/p/figure.html