数据挖掘竞赛kaggle初战——泰坦尼克号生还预测

Posted 2021-11-27 liyaoshi

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据挖掘竞赛kaggle初战——泰坦尼克号生还预测相关的知识，希望对你有一定的参考价值。

1.题目

这道题目的地址在https://www.kaggle.com/c/titanic，题目要求大致是给出一部分泰坦尼克号乘船人员的信息与最后生还情况，利用这些数据，使用机器学习的算法，来分析预测另一部分人员最后是否生还。题目练习的要点是语言和数据分析的基础内容(比如python、numpy、pandas等)以及二分类算法。

数据集包含3个文件：train.csv（训练数据）、test.csv（测试数据）、gender_submission.csv（最后提交结果的示例，告诉大家提交的文件长什么样）

数据集中包含如下数据：

Name	Academy
Survived	0：遇难，1：生还 (这一项只有训练集才有)
pclass	船舱等级
sex	性别
Age	年龄
sibsp	在船上的兄弟姐妹及配偶数
parch	在船上的父母及子女数
ticket	船票编号
fare	船票费用
cabin	船舱号
embarked	乘客登船港口

2.解题步骤

kaggle竞赛的步骤大致如下图
技术图片
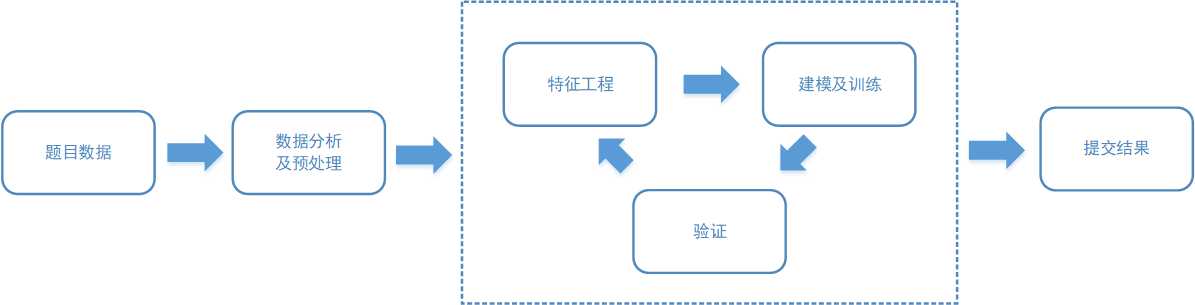
接下来就按照图示，解决Titanic问题

3.数据分析及预处理

这里我使用的环境是anaconda中的jupyter notebook + python3.7 + skilearn

首先读入数据，并查看一下训练集train的数据概况

%matplotlib inline
import numpy as np
import pandas as pd
import re as re

train = pd.read_csv('titanic_data/train.csv')
test  = pd.read_csv('titanic_data/test.csv')
full_data = [train, test]

print (train.info())

在这些数据中，Survived是结果，其余数据中，PassengerId、 Pclass、 Name、 Sex、 SibSp、 Parch、 Ticket、 Fare(测试集Fare有缺失值)是完整的，没有缺失值。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
None

看下测试集的数据

test.head(5)

测试集比训练集少了一项Survived，其余相同。

	PassengerId	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	3	Kelly, Mr. James	male	34.5	0	0	330911	7.8292	NaN	Q
1	893	3	Wilkes, Mrs. James (Ellen Needs)	female	47.0	1	0	363272	7.0000	NaN	S
2	894	2	Myles, Mr. Thomas Francis	male	62.0	0	0	240276	9.6875	NaN	Q
3	895	3	Wirz, Mr. Albert	male	27.0	0	0	315154	8.6625	NaN	S
4	896	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	female	22.0	1	1	3101298	12.2875	NaN	S

这里先把测试集中的PassengerId一列取出，留作后面备用。

PassengerId = test['PassengerId']

打印出训练集的前5项

train.head(5)

先直观看一下数据长什么样

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	373450	8.0500	NaN	S

看一下训练集中数值项(比如Age，结果用一个数值表示)的基本属性

train.describe()

这些属性中就包含很多信息了，包括平均数、中位数，四份位值等等，之后我们会逐项的分析

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

再来看一下非数值项(典型如Name，结果是字母)

train.describe(include=['O'])

从表格中可以得知，Name这个变量是不重复的，没有两个人重名。船票编号和船舱编号都是有重复的。登船港口有三个，大多数人都从S港登船。

	Name	Sex	Ticket	Cabin	Embarked
count	891	891	891	204	889
unique	891	2	681	147	3
top	Kalvik, Mr. Johannes Halvorsen	male	CA. 2343	G6	S
freq	1	577	7	4	644

4.特征工程

了解了数据集的概况，现在我们逐项来分析。首先看pclass这一项，也就是舱位等级

print (train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean())

从表格中可知，不同舱位等级的人生还率相差很大。所以Pclass可选为模型中的一项指标

   Pclass  Survived
0       1  0.629630
1       2  0.472826
2       3  0.242363

再看Sex这一项

print (train[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean())

女性的生还率远高于男性，模型中也加入Sex这一项

      Sex  Survived
0  female  0.742038
1    male  0.188908

现在到了SibSp和Parch，这两项都跟家庭有关，我把这两者先合成一个变量FamilySize，表示家庭人数，再做一个聚合查询

for dataset in full_data:
    dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1

print (train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean())

从数据看，家庭人数是2-4人的时候，生还概率较大。

   FamilySize  Survived
0           1  0.303538
1           2  0.552795
2           3  0.578431
3           4  0.724138
4           5  0.200000
5           6  0.136364
6           7  0.333333
7           8  0.000000
8          11  0.000000

于是我加入了一个新属性FamilyScale，将FamilySize分为三组：独自1人、2-4人和更多。另外还考虑到独自一人和有家庭成员这两种情况区别较大，因此可以另做一个属性IsAlone，来表示乘客是独自一人还是有家庭成员在船。

for dataset in full_data:
    dataset['FamilyScale'] = 0
    dataset['IsAlone'] = 0
    
    dataset.loc[dataset['FamilySize'] == 1, 'FamilyScale'] = 0
    dataset.loc[(dataset['FamilySize'] > 1) & (dataset['FamilySize'] < 4), 'FamilyScale'] = 1
    dataset.loc[dataset['FamilySize'] >= 4, 'FamilyScale'] = 2
    dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1
    
print (train[['FamilyScale', 'Survived']].groupby(['FamilyScale'], as_index=False).mean())
print (train[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean())

对新属性做聚合查询

   FamilyScale  Survived
0            0  0.303538
1            1  0.562738
2            2  0.340659

   IsAlone  Survived
0        0  0.505650
1        1  0.303538

下面是Embarked这一项

freq_port = train.Embarked.dropna().mode()[0]
freq_port

如上面所述，该项的“众数”是‘S’

'S'

因此考虑使用“众数”填充缺失项

for dataset in full_data:
    dataset['Embarked'] = dataset['Embarked'].fillna('S')
print (train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean())

聚合查询结果如下，不同港口登船的生还率有些许差别，这也可以作为模型的一项

  Embarked  Survived
0        C  0.553571
1        Q  0.389610
2        S  0.339009

关于Fare这一项，首先看下它的分布，这里我使用seaborn画图

import seaborn as sns
import matplotlib.pyplot as plt

sns.set_style("whitegrid")
plt.figure(figsize=(8, 6))
sns.distplot(dataset['Fare'], bins=10, rug=False, rug_kws = {'color':'g','lw':2,'alpha':0.5}, kde_kws={"color": "g", "lw": 1.5, 'linestyle':'--'})

图中可以看出，多数人的票价都在一个小的范围内，这种情况下，比较适合采用Fare的中位数进行填充

技术图片

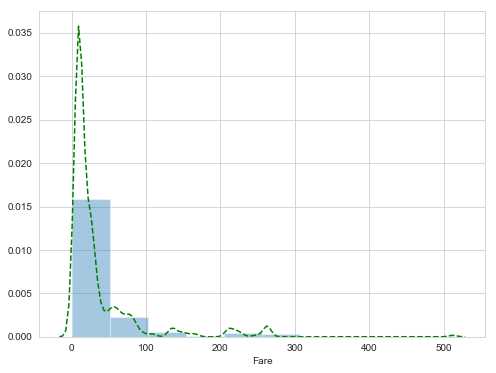
因为Fare这一变量跨度较大，此时可以采用特征工程中常用的“装箱”方法，将数值划入特定的范围。这里采用的是四分位数划分。

for dataset in full_data:
    dataset['Fare'] = dataset['Fare'].fillna(train['Fare'].median())
train['CategoricalFare'] = pd.qcut(train['Fare'], 4)
print (train[['CategoricalFare', 'Survived']].groupby(['CategoricalFare'], as_index=False).mean())


   CategoricalFare  Survived
0   (-0.001, 7.91]  0.197309
1   (7.91, 14.454]  0.303571
2   (14.454, 31.0]  0.454955
3  (31.0, 512.329]  0.581081

Age这一项，还是先看分布图。Age的分布比较像高斯分布，因此可以考虑使用平均值来作为缺失Age的填充。不过不要紧，这里平均值作为一个备选方案，之后可以看一看是否有更好的方案来填充。

plt.figure(figsize=(8, 6))
sns.distplot(dataset['Age'], bins=10, rug=False, rug_kws = {'color':'g','lw':2,'alpha':0.5}, kde_kws={"color": "g", "lw": 1.5, 'linestyle':'--'})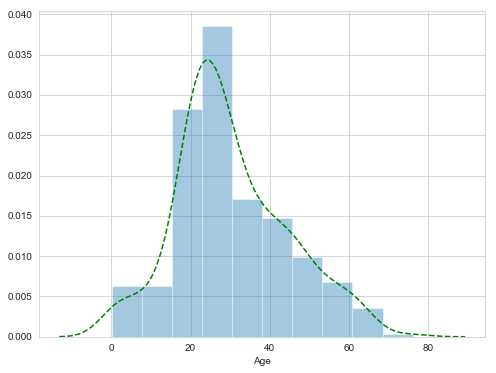

技术图片

Age同样范围较大，依然使用装箱法

train['CategoricalAge'] = pd.cut(train['Age'], 5)
print (train[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean())

结果如下

     CategoricalAge  Survived
0    (0.34, 16.336]  0.550000
1  (16.336, 32.252]  0.369942
2  (32.252, 48.168]  0.404255
3  (48.168, 64.084]  0.434783
4    (64.084, 80.0]  0.090909

下面看Name，歪果仁的名字前面会有Mr、 Miss等称呼，这个和性别、身份等有关，因此引入属性Title提取这个称呼

def get_title(name):
    title_search = re.search(' ([A-Za-z]+)\\.', name)
    # If the title exists, extract and return it.
    if title_search:
        return title_search.group(1)
    return ""

for dataset in full_data:
    dataset['Title'] = dataset['Name'].apply(get_title)

print(pd.crosstab(train['Title'], train['Sex']))

所有的称呼如下

Sex       female  male
Title                 
Capt           0     1
Col            0     2
Countess       1     0
Don            0     1
Dr             1     6
Jonkheer       0     1
Lady           1     0
Major          0     2
Master         0    40
Miss         182     0
Mlle           2     0
Mme            1     0
Mr             0   517
Mrs          125     0
Ms             1     0
Rev            0     6
Sir            0     1

这里借鉴了一些其他选手的思路，将这些Title进一步归类：

for dataset in full_data:
    dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',    'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')

    dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')

print (train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean())

归类后的Title如下，可见生还率确实与Title有一定的相关性

    Title  Survived
0  Master  0.575000
1    Miss  0.702703
2      Mr  0.156673
3     Mrs  0.793651
4    Rare  0.347826

cabin这一项缺失值太多，因此简单粗暴，直接将其分为有值与没有值

train['Has_Cabin'] = train["Cabin"].apply(lambda x: 0 if type(x) == float else 1)
test['Has_Cabin'] = test["Cabin"].apply(lambda x: 0 if type(x) == float else 1)

print (train[['Has_Cabin', 'Survived']].groupby(['Has_Cabin'], as_index=False).mean())

结果如下

   Has_Cabin  Survived
0          0  0.299854
1          1  0.666667

剩下的还有PassengerId与Ticket，这两项是编号属性的，并不能体现什么有用的信息，所以不考虑将它们加入模型

所有的属性都考虑过了，接下来要做的是把非数值属性转化为数值属性，并去掉无用的中间属性与不加入模型的属性。

for dataset in full_data:
    # Mapping Sex
    dataset['Sex'] = dataset['Sex'].map( {'female': 0, 'male': 1} ).astype(int)
    
    # Mapping titles
    title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
    dataset['Title'] = dataset['Title'].map(title_mapping)
    dataset['Title'] = dataset['Title'].fillna(0)
    
    # Mapping Embarked
    dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
    
    # Mapping Fare
    dataset.loc[ dataset['Fare'] <= 7.91, 'Fare']                               = 0
    dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
    dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare']   = 2
    dataset.loc[ dataset['Fare'] > 31, 'Fare']                                  = 3
    dataset['Fare'] = dataset['Fare'].astype(int)

# drop()方法如果不设置参数inplace=True，则只能在生成的新数据块中实现删除效果，而不能删除原有数据块的相应行
# Feature Selection
drop_elements = ['PassengerId', 'Name', 'Ticket', 'Cabin', 'SibSp',                 'Parch', 'FamilySize']
train = train.drop(drop_elements, axis = 1)
train = train.drop(['CategoricalFare', 'CategoricalAge'], axis = 1)

test  = test.drop(drop_elements, axis = 1)

根据目前模型选用的属性，画出热力图，同样使用seaborn绘制。

热力图中的数值是两项属性之间的皮尔森相关系数，用r表示。r描述的是两个变量间线性相关强弱的程度。r的取值在-1与+1之间，若r>0，表明两个变量是正相关；若r<0，表明两个变量是负相关。r 的绝对值越大表明相关性越强。若r=0，表明两个变量间不是线性相关。

这个图主要看这几点：

1.我们选出的变量与Survived这一项的相关性，比如说Sex这一项，相关度比较高，说明这是一个好的标的。在表示家庭的属性中，IsAlone的相关性要比FamilyScale要高，所以最后我会选择IsAlone这一属性代表家庭，去掉FamilyScale。

2.Age属性与Pclass和FamilyScale相关度较高，因此可以使用这两个属性划分群体，对每个群体采用各自的均值进行缺失值填充

sns.set_style("ticks")

colormap = plt.cm.RdBu
plt.figure(figsize=(14,12))
plt.title('Pearson Correlation of Features',y=1.05,size=15)
plt.rcParams['font.size'] =14
sns.heatmap(train.astype(float).corr(),linewidths=0.1,vmax=1.0, square=True, cmap=colormap, linecolor='white', annot=True)
plt.yticks(rotation=360)
plt.show()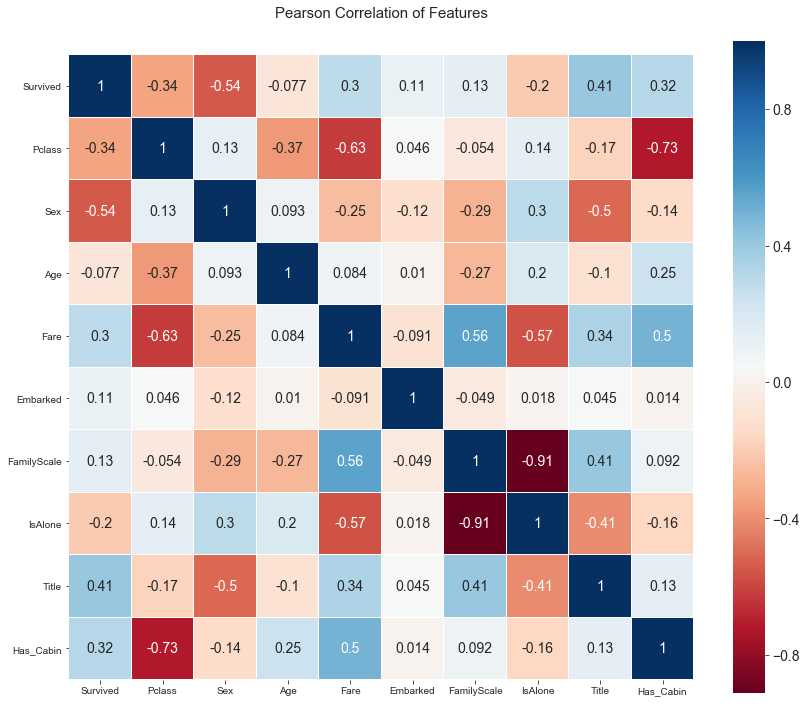

技术图片

填充年龄

guess_ages = np.zeros((3,3))

def fill_age(dataset):
    for i in range(0, 3):
        for j in range(0, 3):
            age_null_count = dataset[(dataset['FamilyScale'] == i) &                                   (dataset['Pclass'] == j+1)]['Age'].isnull().sum()

            guess_df = dataset[(dataset['FamilyScale'] == i) &                                   (dataset['Pclass'] == j+1)]['Age'].dropna()

            age_avg = guess_df.mean()
            age_std = guess_df.std()
            age_null_random_list = np.random.randint(age_avg - age_std, age_avg + age_std, size=age_null_count)

            dataset.loc[(dataset.Age.isnull()) & (dataset.FamilyScale == i) & (dataset.Pclass == j+1), 'Age'] = age_null_random_list

    dataset['Age'] = dataset['Age'].astype(int)
    
    return dataset

train = fill_age(train)
test = fill_age(test)

看下填充之后的结果：

train.head(10)

Out：

	Survived	Pclass	Sex	Age	Fare	Embarked	FamilyScale	IsAlone	Title	Has_Cabin
0	0	3	1	22	0	0	1	0	1	0
1	1	1	0	38	3	1	1	0	3	1
2	1	3	0	26	1	0	0	1	2	0
3	1	1	0	35	3	0	1	0	3	1
4	0	3	1	35	1	0	0	1	1	0
5	0	3	1	19	1	2	0	1	1	0
6	0	1	1	54	3	0	0	1	1	1
7	0	3	1	2	2	0	2	0	4	0
8	1	3	0	27	1	0	1	0	3	0
9	1	2	0	14	2	1	1	0	3	0

对填充完毕的年龄进行聚合：

train['CategoricalAge'] = pd.cut(train['Age'], 5)
print (train[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean())

聚合结果：

  CategoricalAge  Survived
0  (-0.08, 16.0]  0.495652
1   (16.0, 32.0]  0.353201
2   (32.0, 48.0]  0.389121
3   (48.0, 64.0]  0.424658
4   (64.0, 80.0]  0.090909

进行装箱：

for dataset in full_data:
    # Mapping Age
    dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
    dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
    dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
    dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
    dataset.loc[ dataset['Age'] > 64, 'Age']
train = train.drop(['CategoricalAge'], axis = 1)

因为之前用IsAlone属性代表家庭，这里删去FamilyScale

train = train.drop(['FamilyScale'], axis = 1)
test = test.drop(['FamilyScale'], axis = 1)

这时再绘制一下多变量图。主要关注对角线的图，看一下变量分布与Survived之前的关系。比如Fare-Fare的图，可以明显看出Survived=0的Fare是左偏的，Survived=1的Fare是右偏的，这说明票价高低会影响生还几率。

sns.set_style('white')
g = sns.pairplot(train[[u'Survived', u'Pclass', u'Sex', u'Age', u'Fare', u'Embarked',
       u'IsAlone', u'Title', u'Has_Cabin']], hue='Survived', palette = 'seismic',height=1.8, diag_kind = 'kde',diag_kws=dict(shade=True),plot_kws=dict(s=10) )
g.set(xticklabels=[])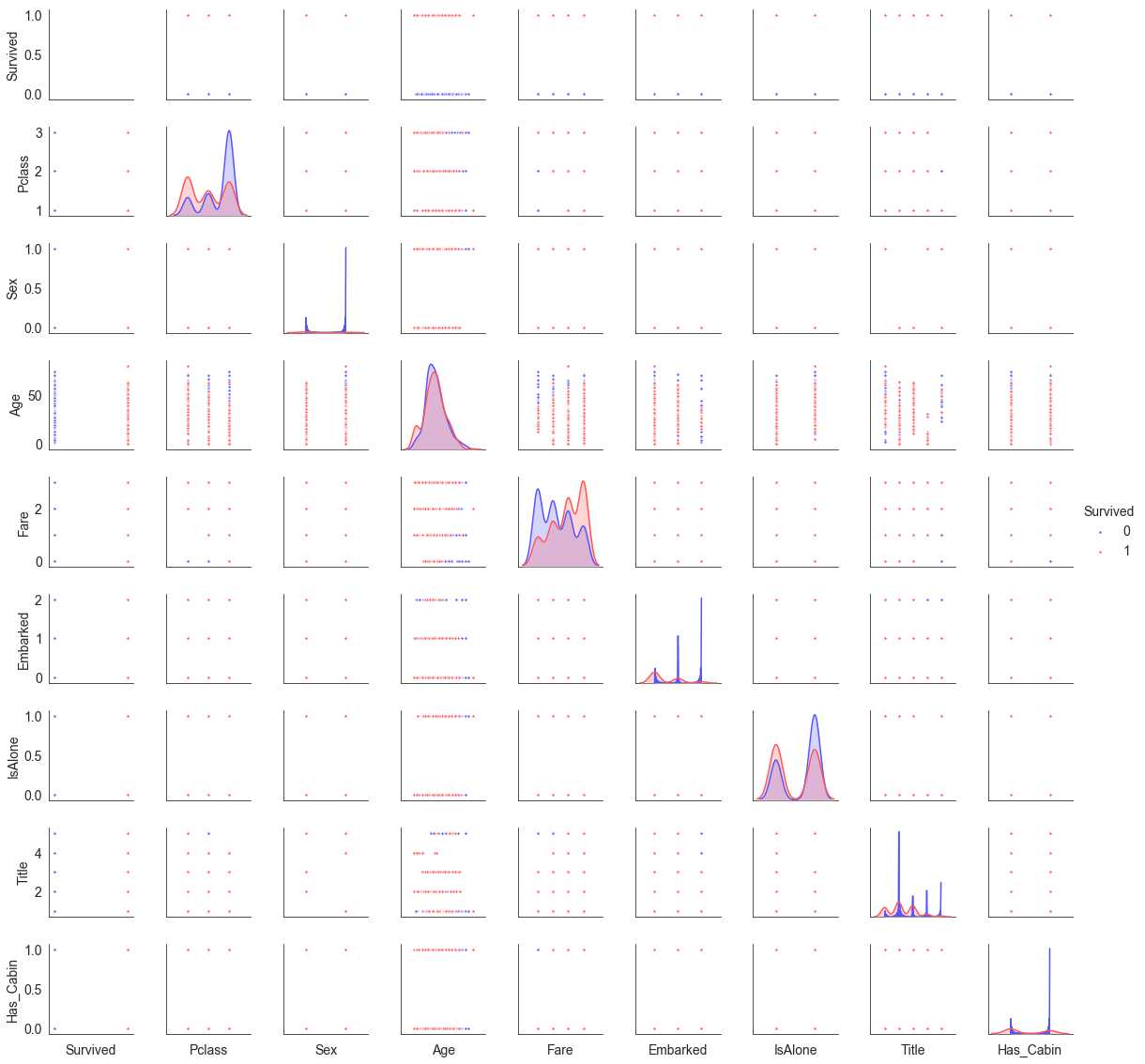

技术图片

5.建模及训练+验证

特征工程到此告一段落，现在开始建模。这里我使用的是xgboost算法，原理可以参考https://xgboost.readthedocs.io/en/latest/tutorials/model.html

引入XGBClassifier

from xgboost import XGBClassifier

将训练集和测试集的DataFrame转为numpy的array

train = train.values
test  = test.values

将训练集中的Survived单独提取出来作为结果(y)：

X = train[0::, 1::]
y = train[0::, 0]

用train_test_split在train上划分训练集和测试集

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

绘制学习曲线函数：

from sklearn.metrics import precision_score

def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
    
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(precision_score(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(precision_score(y_test, y_test_predict))
        
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               train_score, label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               test_score, label="test")
    
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 1])
    plt.show()

学习曲线，由图可见，随着训练样本的增加，train和test的精确度不断地靠近，说明这个模型基本可用。

plot_learning_curve(XGBClassifier(learning_rate=0.01, n_estimators=1500, max_depth=2), X_train, X_test, y_train, y_test)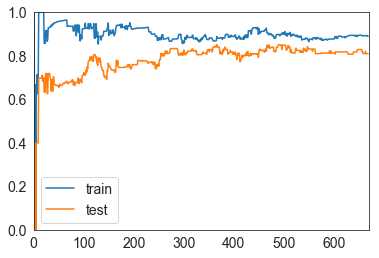

技术图片

将训练数据传入模型：

candidate_classifier = XGBClassifier(learning_rate=0.01, n_estimators=1500, max_depth=2)
candidate_classifier.fit(X, y)

Out：

XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
       colsample_bytree=1, gamma=0, learning_rate=0.01, max_delta_step=0,
       max_depth=2, min_child_weight=1, missing=None, n_estimators=1500,
       n_jobs=1, nthread=None, objective='binary:logistic', random_state=0,
       reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
       silent=True, subsample=1)

生成预测结果：

predictions = candidate_classifier.predict(test)

6.提交结果

生成提交的csv文件：

StackingSubmission = pd.DataFrame({ 'PassengerId': PassengerId,
                            'Survived': predictions })
StackingSubmission.to_csv("Submission_xgb.csv", index=False)

到这里就可以把文件上传kaggle上，来看模型预测的结果得分。如果得分不理想，就需要重新审视一下特征工程，并调整模型的各项参数，进行调优。

以上是关于数据挖掘竞赛kaggle初战——泰坦尼克号生还预测的主要内容，如果未能解决你的问题，请参考以下文章

Kaggle实战入门：泰坦尼克号生还预测（基础版）

kaggle练习项目—泰坦尼克乘客生还预测

泰坦尼克号预测生还案例

Kaggle案例泰坦尼克号问题

Titanic幸存预测分析(Kaggle)

Kaggle竞赛丨入门手写数字识别之KNNCNN降维

	Survived	Pclass	Sex	Age	Fare	Embarked	FamilyScale	IsAlone	Title	Has_Cabin
0	0	3	1	22	0	0	1	0	1	0
1	1	1	0	38	3	1	1	0	3	1
2	1	3	0	26	1	0	0	1	2	0
3	1	1	0	35	3	0	1	0	3	1
4	0	3	1	35	1	0	0	1	1	0
5	0	3	1	19	1	2	0	1	1	0
6	0	1	1	54	3	0	0	1	1	1
7	0	3	1	2	2	0	2	0	4	0
8	1	3	0	27	1	0	1	0	3	0
9	1	2	0	14	2	1	1	0	3	0

	Survived	Pclass	Sex	Age	Fare	Embarked	FamilyScale	IsAlone	Title	Has_Cabin
0	0	3	1	22	0	0	1	0	1	0
1	1	1	0	38	3	1	1	0	3	1
2	1	3	0	26	1	0	0	1	2	0
3	1	1	0	35	3	0	1	0	3	1
4	0	3	1	35	1	0	0	1	1	0
5	0	3	1	19	1	2	0	1	1	0
6	0	1	1	54	3	0	0	1	1	1
7	0	3	1	2	2	0	2	0	4	0
8	1	3	0	27	1	0	1	0	3	0
9	1	2	0	14	2	1	1	0	3	0

	Survived	Pclass	Sex	Age	Fare	Embarked	FamilyScale	IsAlone	Title	Has_Cabin
0	0	3	1	22	0	0	1	0	1	0
1	1	1	0	38	3	1	1	0	3	1
2	1	3	0	26	1	0	0	1	2	0
3	1	1	0	35	3	0	1	0	3	1
4	0	3	1	35	1	0	0	1	1	0
5	0	3	1	19	1	2	0	1	1	0
6	0	1	1	54	3	0	0	1	1	1
7	0	3	1	2	2	0	2	0	4	0
8	1	3	0	27	1	0	1	0	3	0
9	1	2	0	14	2	1	1	0	3	0