Titanic幸存预测分析(Kaggle)

Posted 2020-10-18 jvfjvf

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Titanic幸存预测分析(Kaggle)相关的知识，希望对你有一定的参考价值。

分享一篇kaggle入门级案例，泰坦尼克号幸存遇难分析。

参考文章： 技术世界，原文链接 http://www.jasongj.com/ml/classification/

案例分析内容：

通过训练集分析预测什么人可能生还，并对测试集中乘客做出预测判断

案例分析

加载包

 1 library(dplyr) #bind_rows()
 2 library(ggplot2) #绘图
 3 library(ggthemes)
 4 library(InformationValue) #计算WOE和IV
 5 library(stringr) #数据处理
 6 library(rpart)  #预测乘客年龄
 7 library(scales)  #dollar_format()
 8 library(party)   #cforest()
 9 library(gbm)  #AdaBoost
10 library(MLmetrics) # Mache learning metrics.e.g. Recall, Precision, Accuracy, AUC

加载文件

1 train <- read.csv("F:\\\\R/泰坦尼克幸存分析/train.csv",header = T,stringsAsFactors = F) #ID 1~891乘客信息
2 test <- read.csv("F:\\\\R/泰坦尼克幸存分析/test.csv",header = T,stringsAsFactors = F)  #ID 892~1309号乘客信息(缺少是否存活信息)
3 test_survived <-read.csv("F:/R/泰坦尼克幸存分析/gender_submission.csv",header = T,stringsAsFactors = F)  #ID 892~1309号 是否存活信息

数据整理

1 #合并训练数据和测试数据
2 data <- bind_rows(train,test) 
3 ##Sex:性别,Age:年龄,SibSP:配偶/兄妹数,Parch:父母/子女数,Ticket:船票号
4 ##Fare：费用,Cabin：舱位区域,Pclass:舱位等级,Embarked:到达码头,Title:头衔
5 #将是否存活设为因子
6 data$Survived <- as.factor(data$Survived)
7 train$Survived <-as.factor(train$Survived)
8 test$Survived <- as.factor(test$Survived)

统计幸存和遇难人数是否与舱位等级有关

1 ggplot(data = data[1:nrow(train),],aes(Pclass,..count..,fill=factor(Survived)))+                 #载入训练数据分析
2   geom_bar(stat = \'count\',position = \'dodge\')+        
3   labs(title=\'舱位等级对乘客存活影响\',x=\'舱位等级\',y=\'存活人数\',fill=\'Survived\')+                      #fill为图例标题属性                                
4   scale_fill_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))+                                      #修改图例标签文本
5   scale_x_continuous(breaks=c(1,2,3),labels=c(\'头等舱\',\'二等舱\',\'三等舱\'))+                          #修改X轴刻度文本
6   geom_text(stat = "count",aes(label=..count..),position = position_dodge(width = 1),vjust=-0.3)+ #添加数据标签
7   theme(plot.title = element_text(hjust = 0.5))                                                   #修改标题位置

　　　　　可以看到,头等舱的乘客获救率是最高的，舱位等级越高，获救几率越大

计算舱位等级(Pclass)的WOE和IV

1 class(data$Pclass)  #查看变量(舱位)类型,求WOE时需要转换为因子
2 WOETable(X = factor(data$Pclass[1:nrow(train)]),Y = data$Survived[1:nrow(train)])
3 IV(X = factor(data$Pclass[1:nrow(train)]),Y = data$Survived[1:nrow(train)] )

为了更为定量的计算Pclass的预测价值，可以算出Pclass的WOE和IV如下。从结果可以看出，Pclass的IV为0.5，且“Highly Predictive”。由此可以暂时将Pclass作为　预测模型的特征变量之一。

统计不同title(头衔)的乘客存活率
训练集中给出了乘客姓名，其中含有MR，Capt等常见称号，这通常标志着一个人处于的社会阶层，所以猜测可能与存活率存在一定联系。接下来要进行分类整理。提取出Name中的title标签，并进行分类。

1 data$Title <- sapply(data$Name,FUN=function(x){strsplit(x,split = \'[,.]\')[[1]][2]}) #依次提取出每行的title标签
2 #head(strsplit(data$Name,split = \'[,.]\')[[1]][2])
3 head(data$Title)
4 data$Title <- sub(pattern = \' \',replacement = \'\',data$Title)
5 data$Title[data$Title %in%c(\'Mme\',\'Mlle\')] <-\'Mlle\'
6 data$Title[data$Title %in%c(\'Capt\',\'Don\',\'Major\',\'Sir\')] <-\'Sir\'
7 data$Title[data$Title%in%c(\'Dona\',\'Lady\',\'thhe Countess\',\'Jonkheer\')] <-\'Lady\'
8 data$Title <- factor(data$Title)

抽取完乘客Title后,绘图观察

1 ggplot(data = data[1:nrow(train),],aes(x = Title,y = ..count..,fill=factor(Survived)))+
2   geom_bar(stat = \'count\')+
3   geom_text(stat = \'count\' ,aes(label=..count..),position = position_stack(vjust = 0.85))+
4   labs(title=\'头衔是否影响存活率\',x=\'尊称/头衔\',y=\'人数\',fill=\'Survived\')+
5   theme(plot.title = element_text(hjust =0.55))+
6   scale_fill_discrete(limit=c(0,1),labels=c("遇难","获救"))+
7   theme_economist()

观察图中不难发现，图中Master，Miss,Mlle,Mrs,Ms获救比例均超过50%，而Mr的获救比例不到15.7%。接下来计算WOE和IV，

查看Title这一变量对于最终的预测是否有用

计算头衔(Title)的WOE和IV

　　　　1 WOETable(X = factor(data$Title[1:nrow(train)]),Y = factor(data$Survived[1:nrow(train)]))

　　　 2 IV(X = factor(data$Title[1:nrow(train)]),Y = factor(data$Survived[1:nrow(train)]) )

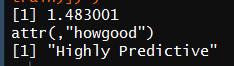
IV为1.520702，且”Highly Predictive”。因此，可暂将Title作为预测模型中的一个特征变量。

猜测性别和存活率有关

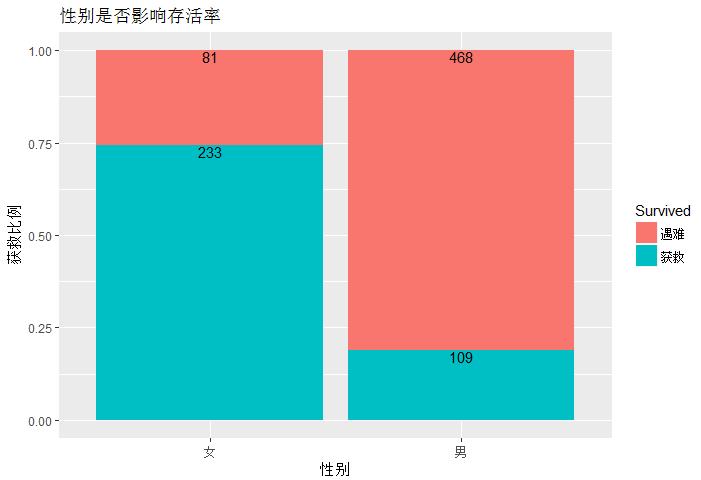
1 ggplot(data = data[1:nrow(train),],aes(x =Sex,y = ..count..,fill=factor(Survived)))+
2   geom_bar(stat=\'count\',position = \'fill\')+
3   geom_text(stat = \'count\',aes(label=..count..),position = \'fill\',vjust=1)+
4   labs(title="性别是否影响存活率",fill="Survived",x=\'性别\',y=\'获救比例\')+
5   scale_x_discrete(breaks = c(\'female\',\'male\'),labels = c(\'女\',\'男\'))+
6   scale_fill_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))

　　　　泰坦尼克号遇难之际，船上乘客秉承‘女士优先’的原则，实际情况是，75%的女性乘客获救，而仅有不到25%的男性乘客获救，这也充分说明了这一原则的真实性。

计算性别(Sex)的WOE和IV

　　　　 WOETable(X = factor(data$Sex[1:nrow(train)]),Y = factor(data$Survived[1:nrow(train)]))

　　　　 IV(X =factor(data$Sex[1:nrow(train)]),Y = factor(data$Survived[1:nrow(train)]) )

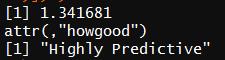
　　　　为高预测变量

统计年龄与存活率是否有关

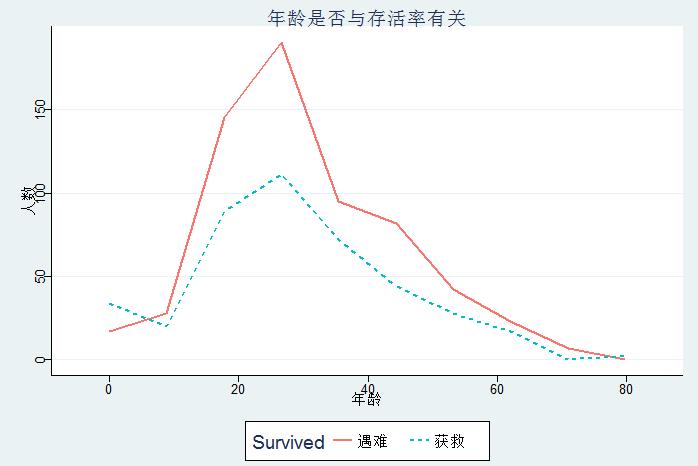
1 summary(data$Age[1:nrow(train)])
2 ggplot(data = data[!is.na(data$Age),],aes(Age,linetype=Survived,color=Survived))+
3   geom_line(stat=\'bin\',bins=10,size=0.8)+
4   labs(title=\'年龄是否与存活率有关\',x=\'年龄\',y=\'人数\',color="Survived",linetype="Survived")+
5   scale_color_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))+
6   scale_linetype_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))+
7   theme_stata()

除了女士优先，老弱人士可能也是优先照顾的对象，图中显示，20岁以下的人员获救比例确实较高，而25岁左右的青年人士获救人数最多，但遇难的人数也接近200人。

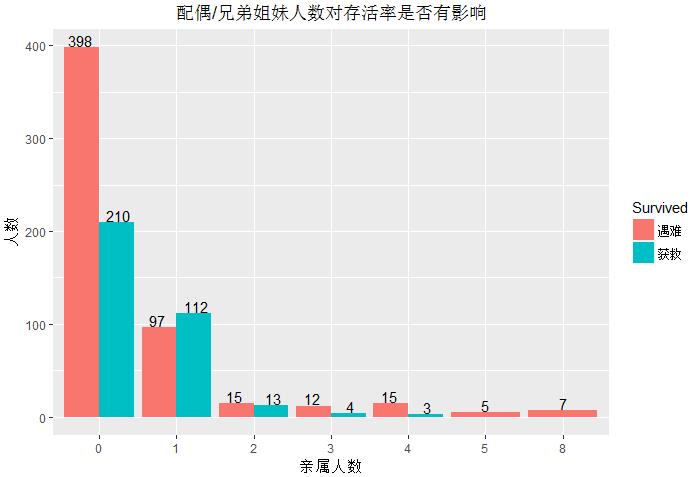
统计(SibSp)配偶/兄弟姐妹人数同时在船对存活率是否有影响

1 ggplot(data = train,aes(x=as.factor(train$SibSp),fill=Survived))+geom_bar(stat=\'count\',position = \'dodge\')+
2   geom_text(stat = \'count\',position = position_dodge(width = 1),aes(label=..count..),vjust=-0.1)+
3   labs(x=\'亲属人数\',y=\'人数\',title=\'配偶/兄弟姐妹人数对存活率是否有影响\')+
4   scale_fill_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))+
5   theme(plot.title = element_text(hjust = 0.5))

训练集中提供了乘客配偶或兄弟姐妹的人数，观察后发现没有亲属在船上的人数较多，沉船时，独身出行的乘客获救几率只有34%，有1~2名配偶或兄弟姐妹同时在船上时，该名乘客获救几率也较高。而人数达 4人以上时，几乎同时遇难。

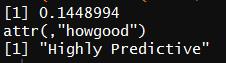
统计SibSp的WOE和IV

　　　　WOETable(X = factor(train$SibSp),Y = factor(train$Survived))

　　　　 IV(X = factor(train$SibSp),Y = factor(train$Survived))

IV为0.1449，为高预测性变量

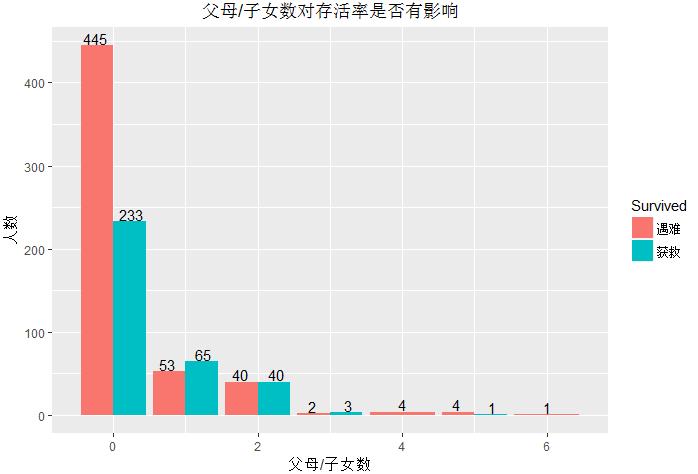
统计Parch(父母/子女人数)对存活率影响

1 ggplot(data = train,aes(Parch,fill=Survived))+
2   geom_bar(stat=\'count\',position = \'dodge\')+
3   labs(title=\'父母/子女数对存活率是否有影响\',x=\'父母/子女数\',y=\'人数\')+
4   geom_text(aes(label=..count..),stat = \'count\',position = position_dodge(width = 1),vjust=-0.1)+
5   scale_fill_discrete(limits=c(0,1),label=c(\'遇难\',\'获救\'))+
6   theme(plot.title = element_text(hjust = 0.5))

Parch列中提供的为乘客的父母/子女人数(同时在船),探究是否该变量会影响存活率。由图可看出，当船上没有自己的父母或者子女时，乘客存活率与SibSp情况相仿，不足1/3。当船上Parch数为1~3人时，获救率高于50%。

计算Parch的WOE和IV

　　　　 WOETable(X = factor(train$Parch),Y = factor(train$Survived))

　　　　 IV(X = factor(train$Parch),Y = factor(train$Survived))

　　　　计算Parch得0.116，认为高预测变量

找出Ticket与存活率关系,共享船票号的可能为一家人,单独船票为独身一人,分成两组进行比较。

1 ticket.count <- aggregate(data$Ticket,by=list(data$Ticket),function(x)sum(!is.na(x)))
2 #整合船票号,记录重复的次数,ticket.count记录这两列(有序),但data中船票号分布是无序的
3 head(ticket.count)
4 data$TicketCount <- apply(X = data,MARGIN = 1,FUN = function(x)ticket.count[which(ticket.count[,1]==x[\'Ticket\']),2])
5 #主体(X)为data,将ticket.count中的船票号(有序)与data$Ticket(无序)进行一一对应
6 head(data$TicketCount)
7 data$TicketCount <- factor(sapply(X = data$TicketCount,FUN = function(x)ifelse(x>1,\'Share\',\'Unique\')))
8 #重复次数>1则说明为共享船票,=1为独自一人.比较两组人员的存活率.

数据集中提供了Ticket列，提供了乘客的船票号。整合船票号，发现存在重复的船票号，猜想可以与家庭共享船票号有关。前面得存活率与SibSP和Parch有关，现可将Ticket分成两类，一类为家庭共享船票，一类为独自乘船所用船票号。

　　 1 #重复次数>1则说明为共享船票,=1为独自一人.比较两组人员的存活率.
　　 2 ggplot(data,aes(TicketCount,..count..,fill=factor(Survived)))+
　　 3   geom_bar(stat = \'count\',position = \'dodge\')+
　　 4   labs(title=\'船票号与存活率联系\',x=\'船票号\',y=\'人数\',fill=\'Survived\')+
　　 5   geom_text(stat = \'count\',aes(label=..count..),position = position_dodge(width = 0.9),vjust=-0.1)+
　　 6   scale_fill_discrete(limits=c(0,1),labels=c(\'遇难\',\'获救\'))+
　　 7   theme(plot.title = element_text(hjust = 0.5))

　　　　图可看出，共用一张船票的家庭，存活率为50%，而单张船票(即独自出行)的乘客，遇难的可能性高达73%

计算TicketCount的WOE和IV

1  WOETable(X = factor(data$TicketCount),Y = factor(data$Survived))
##      CAT GOODS BADS TOTAL     PCT_G     PCT_B        WOE        IV
## 1  share   308  288   596 0.6234818 0.3533742  0.5677919 0.1533649
## 2 unique   186  527   713 0.3765182 0.6466258 -0.5408013 0.1460745

1 > IV(X = factor(data$TicketCount),Y = factor(data$Survived))
## [1] 0.2994394
## attr(,"howgood")
## [1] "Highly Predictive"

IV为0.29，且为Highly Predictive　

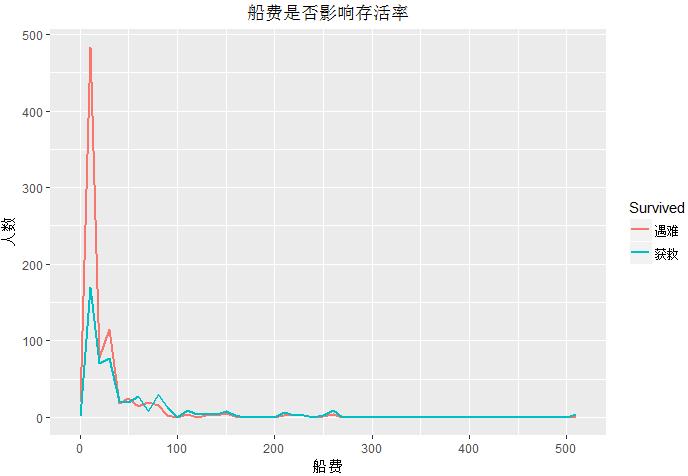
统计船费(Fare)和存活率关系

　　　　船费与舱位等级和行程距离有关，已知存活率与舱位等级(Pclass)存在一定关系,猜想船费可能也存在关系　　

　　 1 summary(data$Fare)
　　 2 class(data$Fare)
　　 3 ggplot(data[!is.na(data$Fare),],aes(x = Fare,color=factor(Survived)))+geom_line(stat = \'bin\',binwidth=10,size=1)+
　　 4   labs(title=\'船费是否影响存活率\',x=\'船费\',y=\'人数\',color=\'Survived\')+
　　 5   scale_color_discrete(labels=c(\'遇难\',\'获救\'))+
　　 6   theme(plot.title = element_text(hjust=0.5))

　　　　　　由图可看出，船费超过100元的乘客几乎都获救　　　　

计算Fare的WOE和IV

　　　　 WOETable(X = factor(data$Fare),Y = data$Survived) 　

　　　　IV(X = factor(data$Fare),Y = data$Survived)
　　　　[1] 0.709573
　　　　attr(,"howgood")
　　　　[1] "Highly Predictive"

　　　　　　同样Fare为高预测变量

统计舱位区域(Carbin)对存活率影响

　　　　对于Cabin变量，其值以字母开始，后面伴以数字。这里有一个猜想，字母代表某个区域，数据代表该区域的序号。类似于火车票即有车箱号又有座位号。因此，这里可尝试将Cabin的首字母提取出来，并分别统计出不同首字母仓位对应的乘客的幸存率。

　　 1 data$Cabin_level <- substr(x = data$Cabin,start = 1,stop = 1)
　　 2 ggplot(data,aes(data$Cabin_level,fill=Survived))+geom_bar(stat = \'count\',position = \'dodge\')+
　　 3   geom_text(stat = \'count\', aes(label=..count..),position = position_dodge(width = 1),vjust=-0.1)+
　　 4   labs(title=\'舱位区域对存活率影响\',x=\'舱位\',y=\'人数\')+
　　 5   scale_fill_discrete(label=c(\'遇难\',\'获救\'))

　　　　Cabin变量中存在的空字符串较多，分析其他得B,C,D,E舱的乘客幸存率远高于50%，其他舱的乘客则低于50%。

计算data$Cabin_level的WOE和IV

　　　　WOETable(X = factor(data$Cabin_level),Y = data$Survived)

　　　　 IV(X = factor(data$Cabin_level),Y = data$Survived)

统计登船码头是否与存活率有关

1 ggplot(train,aes(Embarked,fill=Survived))+geom_bar(stat = \'count\',position = \'dodge\')+
2   geom_text(stat = \'count\',aes(label=..count..),position = position_dodge(width = 1),vjust=-0.1)

　　　　到达C码头的乘客获救率高于50%，而到达S码头的乘客遇难人数达427人，幸存率仅有29%　　　　

计算Embarked(登船码头)WOE和IV

列出所有缺失数据

　　　　研究完变量后，接下来要对缺失数据进行处理

 1 attach(data)
 2 head(missing)
 3 missing<- list(Pclass=nrow(data[is.na(Pclass),]))
 4 missing$Name <- nrow(data[is.na(Name),])
 5 missing$Sex <- nrow(data[is.na(Sex),])
 6 missing$Age <- nrow(data[is.na(Age),])
 7 missing$SibSp <-  nrow(data[is.na(SibSp),])
 8 missing$Parch <-  nrow(data[is.na(Parch),])
 9 missing$Ticket <-  nrow(data[is.na(Ticket),])
10 missing$Fare <-  nrow(data[is.na(Fare),])
11 missing$Cabin <- nrow(data[which(data$Cabin==\'\'),])
12 missing$Embarked <-  nrow(data[which(data$Embarked==\'\'),])
13 #names(missing)
14 #missing[["Cabin"]][1]
15 for (name in names(missing)) {
16   if(missing[[name]][1]>0){
17     print(paste(\'\',name,\' miss \',missing[[name]][1],\' values\',sep=\'\'))
18   }
19 }
20 detach(data)

预测乘客年龄

　　　　　　乘客年龄数据共缺失263条，缺失量较大，不适合使用中位数或均值填补，通过使用其它变量预测或者直接将缺失值设置为默认值的方法填补，这里通过其它变量来预测缺失的年龄信息。

　　　　1 age.model <- rpart(Age~Pclass+factor(Sex)+SibSp+Parch+Fare+factor(Embarked)+Title,data = data[!is.na(data$Age),],method = \'anova\')
　　　　2 data$Age[is.na(data$Age)]
　　　　3 data$Age[is.na(data$Age)] <- predict(age.model,data[is.na(data$Age),])

中位数填补缺失的Embarked值

　　　　　　查看缺失码头,发现船费都为80,猜想船费与舱位和到达码头有关。绘图查看后发现到达码头C的头等舱船票为80,可以将该缺失的空值补为C

　　　　1 ggplot(data[which(data$Embarked!=\'\'),],aes(Embarked,Fare,fill=factor(Pclass)))+
　　　　2   geom_boxplot()+
　　　　3   geom_hline(yintercept = 80,color=\'red\',linetype=2,lwd=1)+
　　　　4   scale_y_continuous(labels = dollar_format())+
　　　　5   labs(title=\'船费和舱位及登船码头的关系\',x=\'登船码头\',y=\'船费\',fill=\'舱位等级\')+
　　　　6   theme(plot.title = element_text(hjust=0.5),panel.grid.major = element_blank())+
　　　　7   scale_fill_discrete(label=c(\'头等舱\',\'二等舱\',\'三等舱\'))

　　　　　　　　 1 data$Embarked[which(data$Embarked==\'\')] <- \'C\'

　　　　　　　　　 2 data$Embarked <- as.factor(data$Embarked) 　　　　　　

补船费的缺失值

　　　　船费和舱位等级，到达码头存在联系，已知另外两个条件，不难猜出船费为多少，将缺失的船费的数据补齐

　　　　1 data[is.na(data$Fare),c(\'Pclass\',\'Embarked\')]
　　　　2 summary(data[which(data$Pclass==\'3\'&&data$Embarked==\'S\'),\'Fare\'])
　　　　3 data[is.na(data$Fare),\'Fare\'] <-7.25

补Cabin(设为默认值)

　　　　　　因为除去这些缺失值后,测得IV已较高,所以可直接设为一个默认值

　　　　1 summary(data$Cabin)
　　　　2 head(data$Cabin)
　　　　3 data$Cabin <- as.factor(sapply(data$Cabin,FUN = function(x) ifelse(x==\'\',\'X\',str_sub(x,1,1))))

训练模型

1 set.seed(123)
2 class(data$Embarked)
3 data$Sex <- as.factor(data$Sex)
4 model <- cforest(Survived~Pclass+Title+Sex+Age+SibSp+Parch+TicketCount+Fare+Cabin+Embarked,data,controls = cforest_unbiased(ntree=2000,mtry=3)

交叉验证

1 cv.summarize <- function(data.true, data.predict) {
2   print(paste(\'Recall:\', Recall(data.true, data.predict)))
3   print(paste(\'Precision:\', Precision(data.true, data.predict)))
4   print(paste(\'Accuracy:\', Accuracy(data.predict, data.true)))
5   print(paste(\'AUC:\', AUC(data.predict, data.true)))

预测

1 predict.result <-predict(model,data[(1+nrow(train)):(nrow(data)),],OOB=TRUE,type=\'response\')
2 output <- data.frame(PassengerID=test$PassengerId,Survived=predict.result)
3 write.csv(output,file =\'F:/R/泰坦尼克幸存分析/cit1.csv\',row.names = FALSE)

以上是关于Titanic幸存预测分析(Kaggle)的主要内容，如果未能解决你的问题，请参考以下文章

kaggle入门之Titanic生存预测

Titanic生存预测（Kaggle入门赛）——基于R语言

kaggle Titanic心得

kaggle入门题Titanic

kaggle入门项目：Titanic存亡预测数据处理

kaggle入门项目：Titanic存亡预测验证与实现

Titanic幸存预测分析(Kaggle)

案例分析内容：

案例分析

加载包

加载文件

数据整理

统计幸存和遇难人数是否与舱位等级有关

计算舱位等级(Pclass)的WOE和IV

统计不同title(头衔)的乘客存活率

抽取完乘客Title后,绘图观察

计算头衔(Title)的WOE和IV

猜测性别和存活率有关

计算性别(Sex)的WOE和IV

统计年龄与存活率是否有关

统计(SibSp)配偶/兄弟姐妹人数同时在船对存活率是否有影响

统计SibSp的WOE和IV

统计Parch(父母/子女人数)对存活率影响

计算Parch的WOE和IV

找出Ticket与存活率关系,共享船票号的可能为一家人,单独船票为独身一人,分成两组进行比较。

计算TicketCount的WOE和IV

统计船费(Fare)和存活率关系

计算Fare的WOE和IV

统计舱位区域(Carbin)对存活率影响

计算data$Cabin_level的WOE和IV

统计登船码头是否与存活率有关

计算Embarked(登船码头)WOE和IV

列出所有缺失数据

预测乘客年龄

中位数填补缺失的Embarked值

补船费的缺失值

补Cabin(设为默认值)

训练模型

交叉验证

预测