kaggle练习项目—泰坦尼克乘客生还预测

Posted 2021-01-02 lengjie

一、问题复述

　　泰坦尼克号是一艘英国皇家邮轮，在当时是全世界最大的海上船舶。1912年4月，该邮轮在首航中碰撞上冰山后沉没。造成船上2224名人员中1514人罹难。

　　现在根据乘客的船舱等级、性别、年龄等信息，对其是否获救进行判定。我们一共有1309名乘客的信息，其中891名乘客信息作为训练集，另外418名乘客信息作为测试集。

　　先查看数据的总体情况：

# -*- coding: utf-8 -*-

import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import matplotlib.pyplot as plt

plt.rcParams[‘font.sans-serif‘]=[‘SimHei‘]  #用来正常显示中文标签
plt.rcParams[‘axes.unicode_minus‘]=False    #用来正常显示负号

pd.set_option(‘display.width‘, 2000, ‘display.max_rows‘, None,‘display.max_columns‘, None)  # 设置数据显示
trd=pd.read_csv("../data/train.csv")                   # 读取训练数据
tsd=pd.read_csv("../data/test.csv")                    # 读取测试数据
trd.info()                                       # 读取训练数据列信息
tsd.info()                                       # 读取测试数据列信息
print(trd.describe())                       # 显示训练数据特征
print(tsd.describe())                       # 显示测试数据特征

　　

　可看到包含如下属性：

　　PassengerId（乘客编号），训练集：1-891，测试集：892-1309；

　　Survived（是否获救），是用1表示，否用0表示，只训练集中有该项属性；

　　Pclass（船舱等级），分为1、2、3级；

　　Name（乘客姓名）；

　　Sex（乘客性别），female，male；

　　Age（乘客年龄），训练集：714名乘客有该项属性，177名乘客缺失，测试集：332名乘客有该项属性，86名乘客缺失；

　　SibSp（兄弟姐妹配偶个数）；

　　Parch （父母子女个数）；

　　Ticket （船票信息），每名乘客均不同，由数字编号，字母等组成，十分杂乱；

　　Fare（船票价格）；

　　Cabin（船舱编号） ， 由单个大写字母+数字组成，训练集：204名乘客有该项属性，687名乘客缺失；测试集：91名乘客有该项属性，241名乘客缺失。

　　Embarked（登船口），分别有C、S、Q三个登船口，训练集中两名乘客缺失该项信息。

 

二、数据初步分析

　　每位乘客的信息中，优先考虑数据质量相对较高的数值属性、标称属性等。对于PassengerId、Name、Ticket这3项暂时不做分析，另外8项属性，首先独立地分析每个属性对乘客获救与否的影响。

# -*- coding: utf-8 -*-

import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import matplotlib.pyplot as plt

plt.rcParams[‘font.sans-serif‘]=[‘SimHei‘]  #用来正常显示中文标签
plt.rcParams[‘axes.unicode_minus‘]=False    #用来正常显示负号

pd.set_option(‘display.width‘, 2000, ‘display.max_rows‘, None,‘display.max_columns‘, None)  # 设置数据显示
trd=pd.read_csv("../data/train.csv")    # 读取数据
trd.info()                              # 读取列信息
# print(trd.describe())                 # 显示特征值

# 两个Series，将一个索引处有值另一个为NaN的地方填充为0
def func1(Series1,Series2):
    for i in Series1.index:
        if i not in Series2.index:
            Series2[i]=0
    for i in Series2.index:
        if i not in Series1.index:
            Series2[1] = 0
    return Series1,Series2

# begin -*- 6.2属性与获救结果的关联统计 -*-
fig=plt.figure(figsize=(12,6))        # 定义图并设置画板尺寸
fig.set(alpha=0.2)                    # 设定图表颜色alpha参数
# fig.tight_layout()                  # 调整整体空白
plt.subplots_adjust(left=0.08,right=0.94,wspace =0.36, hspace =0.5)       # 调整子图间距

#1 各船舱等级的获救情况
ax1=fig.add_subplot(241)
ax1.set(title=u"各船舱等级乘客获救情况",xlabel=u"船舱等级",ylabel=u"人数")
ax1.set_title(u"各船舱等级乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax1.axis([0,4,0,600])
S0_Pclass= trd.Pclass[trd.Survived == 0].value_counts()
S1_Pclass= trd.Pclass[trd.Survived == 1].value_counts()
plt.xticks(rotation=90)
dfp1=pd.DataFrame({u‘未获救‘:S0_Pclass, u‘获救‘:S1_Pclass}).plot(ax=ax1,kind=‘bar‘, stacked=True,rot=1)
for i in S0_Pclass.index:                                                                   # 添加列标签
    plt.text(i-1.16,S0_Pclass[i]+S1_Pclass[i]+12,"{:.2f}".format(S1_Pclass[i]/(S0_Pclass[i]+S1_Pclass[i])))


#2 各船舱号乘客获救情况
ax2=fig.add_subplot(242)
ax2.set(title="各船舱号乘客获救情况",xlabel=u"船舱号",ylabel=u"人数")
ax2.set_title(u"各船舱号乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax2.axis([0,8,0,800])
trd2=trd.copy()
count=0
for i in trd2.Cabin.fillna("N").values:
    trd2.Cabin[count]=i[0]
    count+=1
S0_Cabin=trd2.Cabin[trd2.Survived==0].value_counts()
S1_Cabin=trd2.Cabin[trd2.Survived==1].value_counts()
dfp2=pd.DataFrame({"未获救":S0_Cabin,"获救":S1_Cabin}).plot(ax=ax2,kind="bar",stacked=True,rot=1)
S0_Cabin,S1_Cabin=func1(S0_Cabin,S1_Cabin)
S0_Cabin,S1_Cabin=S0_Cabin.sort_index(),S1_Cabin.sort_index()
count2=-0.5
for i in S0_Cabin.index:
    # print(i,S0_Cabin.index,S0_Cabin[i])
    # print(ax2.get_xticks())
    plt.text(count2,S0_Cabin[i]+S1_Cabin[i]+16,"{:.1f}".format(S1_Cabin[i]/(S0_Cabin[i]+S1_Cabin[i])))
    count2+=1

#3 各登船口的获救情况
ax3=fig.add_subplot(243)
ax3.set(title=u"各登船口乘客获救情况",xlabel=u"登船口",ylabel=u"人数")
ax3.set_title(u"各登船口乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax3.axis([0,3,0,800])
S0_Embarked= trd.Embarked[trd.Survived == 0].value_counts()
S1_Embarked= trd.Embarked[trd.Survived == 1].value_counts()
dfp2=pd.DataFrame({u‘未获救‘:S0_Embarked, u‘获救‘:S1_Embarked}).plot(ax=ax3,kind=‘bar‘, stacked=True,rot=1)
c=0
for i in S0_Embarked.index:                                                                   # 添加列标签
    plt.text(c-0.2,S0_Embarked[i]+S1_Embarked[i]+20,"{:.2f}"             .format(S1_Embarked[i]/(S0_Embarked[i]+S1_Embarked[i])))
    c+=1

#4 各船票价格乘客的获救情况
ax4=fig.add_subplot(244)
ax4.set(title="各船票价格乘客的获救情况",xlabel=u"票价",ylabel=u"获救率")
ax4.set_title(u"各船票价格乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax4.axis([0,300,0,1])
x=np.array(sorted(trd.Fare[trd.Fare.notnull()]))
y=[]
for i in x:
    y.append(trd.Fare[trd.Fare < i][trd.Survived == 1].count()/trd.Fare[trd.Fare < i].count())
y=np.array(y)
plt.plot(x,y,"--",linewidth=0.6)
    # ax4.set_xticks([])                                                   # 不显示x轴刻度

#5 各性别的获救情况
ax5=fig.add_subplot(245)
ax5.set(title=u"不同性别乘客获救情况",xlabel=u"性别",ylabel=u"人数")
ax5.set_title(u"不同性别乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax5.axis([0,5,0,700])
S0_Sex=trd.Sex[trd.Survived==0].value_counts()
S1_Sex=trd.Sex[trd.Survived==1].value_counts()
dfp3=pd.DataFrame({u‘未获救‘:S0_Sex, u‘获救‘:S1_Sex}).plot(ax=ax5,kind=‘bar‘, stacked=True,rot=0)
c=1
for i in S0_Sex.index:                                                                   # 添加列标签
    plt.text(c-0.15,S0_Sex[i]+S1_Sex[i]+16,"{:.2f}".format(S1_Sex[i]/(S0_Sex[i]+S1_Sex[i])))
    c-=1

#6 各年龄乘客的获救情况
ax6=fig.add_subplot(246)
ax6.set(title="各年龄乘客获救情况",xlabel=u"乘客年龄",ylabel=u"获救率")
ax6.set_title(u"各年龄乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
x6=np.array(sorted(trd.Age[trd.Age.notnull()]))
# print(x6)
y6=[]
for i6 in x6:
    y6.append(trd.Age[trd.Age<i6][trd.Survived==1].count()/trd.Age[trd.Age<i6].count())
plt.plot(x6,y6,"--",linewidth=0.6)
    # ax6.set_xticks([])                                                   # 不显示x轴刻度

#7 登船兄弟姐妹配偶人数-乘客获救情况
ax7=fig.add_subplot(247)
ax7.set(title=u"登船兄弟姐妹配偶人数-乘客获救情况",xlabel=u"登船兄弟姐妹配偶人数",ylabel=u"人数")
ax7.set_title(u"登船兄弟姐妹配偶人数-乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax7.axis([0,10,0,700])
S0_SibSp=trd.SibSp[trd.Survived==0].value_counts()
S1_SibSp=trd.SibSp[trd.Survived==1].value_counts()
dfp4=pd.DataFrame({"未获救":S0_SibSp,"获救":S1_SibSp}).plot(ax=ax7,kind="bar",stacked=True,rot=1)
S0_SibSp,S1_SibSp=func1(S0_SibSp,S1_SibSp)                      # 加起来
S0_SibSp=S0_SibSp.sort_index()                                  # 按照索引排序
S1_SibSp=S1_SibSp.sort_index()
c=0
for i in S0_SibSp.index:                                                                   # 添加列标签
    plt.text(c-0.3,S0_SibSp[i]+S1_SibSp[i]+16,"{:.2f}".format(S1_SibSp[i]/(S0_SibSp[i]+S1_SibSp[i])))
    c+=1

#8 登船父母子女人数-乘客获救情况
ax8=fig.add_subplot(248)
ax8.set(title=u"登船父母子女人数-乘客获救情况",xlabel=u"登船父母子女人数",ylabel=u"人数")
ax8.set_title(u"登船父母子女人数-乘客获救情况",fontdict={‘fontsize‘:10})                # 设置标题字体大小
ax8.axis([0,10,0,800])
S0_Parch=trd.Parch[trd.Survived==0].value_counts()
S1_Parch=trd.Parch[trd.Survived==1].value_counts()
dfp8=pd.DataFrame({"未获救":S0_Parch,"获救":S1_Parch}).plot(ax=ax8,kind="bar",stacked=True,rot=0.5)
S0_Parch,S1_Parch=func1(S0_Parch,S1_Parch)                      # 加起来
S0_Parch=S0_Parch.sort_index()                                  # 按照索引排序
S1_Parch=S1_Parch.sort_index()
c=0
for i in S0_Parch.index:                                                                   # 添加列标签
    plt.text(c-0.3,S0_Parch[i]+S1_Parch[i]+16,"{:.2f}".format(S1_Parch[i]/(S0_Parch[i]+S1_Parch[i])))
    c+=1

plt.savefig(‘../result/数据初步分析.jpg‘)
plt.show()

　　

　　得到如下图所示结果，对8个子图逐一进行解释和分析（子图编号按照从左至右，先行后列排序）。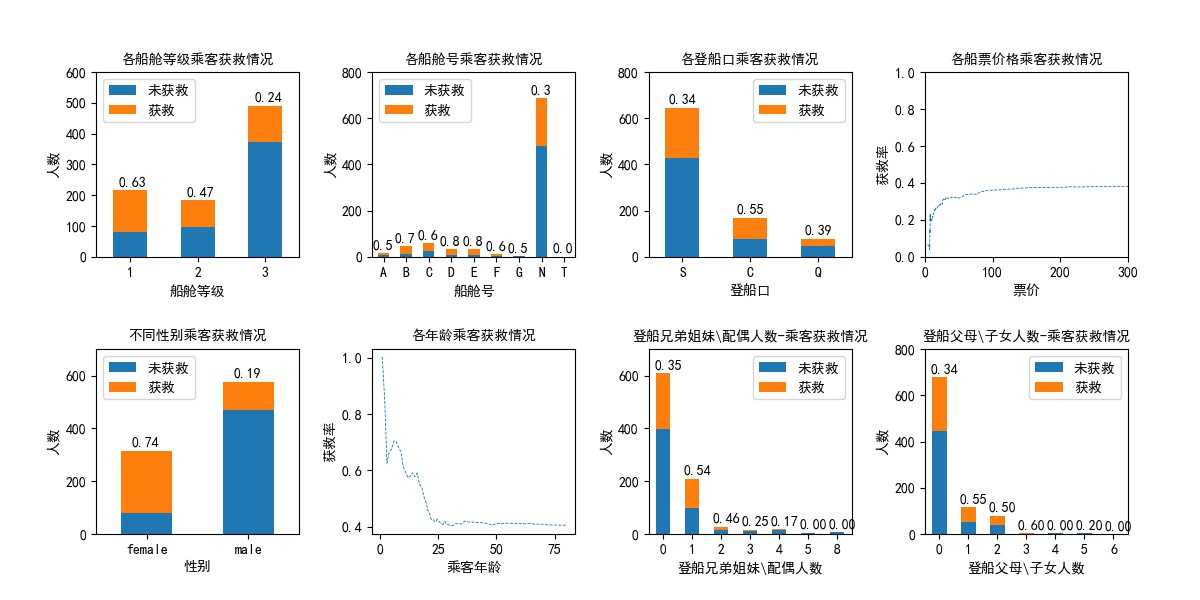

　　子图1，船舱不同等级乘客获救情况。共有3个等级，图上标签表示存活率。由图可知，船舱等级为1、2、3的乘客获救率分别为0.64、0.47、0.24。因此，船舱等级是一个较显著的影响因素。

　　子图2，由于各乘客船舱号是大写字母加数字，且大部分乘客缺失该项属性，尝试以船舱号首字母将其分类，并以N表示该项缺失。由子图2可知，缺失该项属性的乘客存活率为0.3，其它乘客存活率在0.5-0.8之间，且未缺失该项属性的乘客每类样本量均较小。因此在后续分析中，该项属性以是否缺失作为分类标准。

　　子图3，从S、C、Q登船口登船的乘客获救率分别为0.34、0.55、0.39。

　　子图4，票价-存活率的概率分布，即横坐标为票价，纵坐标为低于该票价的乘客的存活率。可以看出，票价越高，获救率越大。

　　子图5，按照乘客性别考查获救率，可以看出女性乘客获救率0.74，明显高于男性0.19的获救概率。是一个较显著的影响因素。

　　子图6，年龄-存活率的概率分布，即横坐标为年龄，纵坐标为小于该年龄的乘客的存活率。可以看出，年龄越小，获救率越大。

　　子图7，按照同登船的兄弟姐妹配偶个数考查，该属性值为0、1、2的乘客获救率分别为0.35、0.54、0.46，其它取值的乘客样本量较小，且获救率较低，可以归为一类。

　　子图8，按照同登船的父母子女个数考查，该属性值为0、1、2的乘客获救率分别为0.34、0.55、0.50，其它取值的乘客样本量较小，且获救率较低，可以归为一类。

 

三、数据预处理

　　通过以上分析，我们大致了解了各属性对乘客获救与否的影响，现对各属性作如下预处理：

　　船舱号：缺失该项属性标记为0，未缺失标记为1

　　登船口：缺失、C、S、Q分别标记为0、1、2、3

　　船票价格： 规范化（按照比例映射到[0,1]区间内）

　　性别：female标记为0，male标记为1

　　年龄：利用随机森林和其它属性填补缺失数据，再对其规范化（按照比例映射到[0,1]区间内）

　　登船兄弟姐妹配偶人数：大于等于3个统一记为3，其余不变

　　登船父母子女人数：大于等于3个统一记为3，其余不变

　　

# 数据数值化
def data_sd(trd):
    trd.loc[(trd.Cabin.notnull()), ‘Cabin‘] = 1
    trd.loc[(trd.Cabin.isnull()), ‘Cabin‘] = 0
    trd.loc[(trd[‘SibSp‘]>=3), ‘SibSp‘] = 3
    trd.loc[(trd[‘Parch‘]>=3),‘Parch‘] = 3
    trd.Sex[trd.Sex=="female"]=0
    trd.Sex[trd.Sex=="male"]=1
    trd.Embarked[trd.Embarked=="C"]=0
    trd.Embarked[trd.Embarked=="S"]=1
    trd.Embarked[trd.Embarked=="Q"]=2
    trd.Embarked[trd.Embarked.isnull()]=3
data_sd(trd)       # 训练数据数值化
data_sd(tsd)       # 测试数据数值化

# 随机森林填补缺失的年龄属性
def set_missing_ages(df):
    df1= df[[‘Age‘, ‘Pclass‘, ‘Fare‘, "Embarked",‘Cabin‘,‘Parch‘, ‘SibSp‘]][df.Fare.notnull()]  # 提取特征较显著的几个属性数据
    y = df1[df1.Age.notnull()].values[:, 0]    # 提取有年龄乘客的年龄数据
    x = df1[df1.Age.notnull()].values[:, 1:]   # 提取有年龄乘客的其它属性数据
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)  # 定义随机森林
    rfr.fit(x, y)                              # 进行训练
    predictedAges = rfr.predict(df1[df1.Age.isnull()].values[:, 1:])  # 进行预测。
    df.loc[(df.Age.isnull()), ‘Age‘] = predictedAges                  # 用得到的预测结果填补原缺失数据
    return df, rfr
trd, rfr = set_missing_ages(trd)                   # 调用年龄填补函数
trd.Age=trd.Age.astype(np.int32)                   # 年龄数据换为整数
tsd, rfr = set_missing_ages(tsd)                   # 调用年龄填补函数
tsd.Age=tsd.Age.astype(np.int32)                   # 年龄数据换为整数


# 年龄数据规范化
import sklearn.preprocessing as prc
def data_asd(trd):
    mmsc= prc.MinMaxScaler(feature_range=(0, 1))    # 年龄数据规范区间（0，1）
    T=np.array([trd.Age]).transpose()               # 年龄数据加维、数组化、取转置。才能顺利进行规范化操作。
    trd_d=mmsc.fit_transform(T).transpose()[0]      # 数据规范化，转置回来，取一维。
    trd["Age_mmsc"]=trd_d                           # 规范化的年龄数据拼接到原数据
data_asd(trd)
data_asd(tsd)


# 票价数据规范化
def data_fsd(trd):
    trd.Fare[trd.Fare.isnull()]=trd.Fare.mean()      # 空缺票价填充为平均值
    mmsc= prc.MinMaxScaler(feature_range=(0, 1))     # 票价数据规范区间（0，1）
    T=np.array([trd.Fare]).transpose()               # 票价数据加维、数组化、取转置。才能顺利进行规范化操作。
    trd_d=mmsc.fit_transform(T).transpose()[0]       # 数据规范化，转置回来，取一维。
    trd["Fare_mmsc"]=trd_d                           # 规范化的票价数据拼接到原数据
data_fsd(trd)
data_fsd(tsd)

　

四、建模及结果输出　

　对于8个属性，一共可以有$c^1_8+c^2_8+...+c^8_8=255$种特征组合。对每种特征组合，我们用训练集进行交叉验证，并在指定标准差范围内，选取出平均分最高的特征组合。

　　采用k-邻近算法、逻辑回归、SVM、决策树等方法进行建模，下面为k-邻近算法代码，其余方法代码框架与其类似：

# k-邻近算法
score=[]                  # 记录评分的列表
temp0=[]                  # 记录当前选取的特征组合的评分
temp1=0                   # 记录当前选取组合的平均分数
temp2=0                   # 记录当前选取组合的分数标准差
z=["Pclass","Sex","Embarked","Age_mmsc","Cabin","Fare_mmsc",‘SibSp‘,‘Parch‘]        # 用于生成特征组合的完整属性列表
for j in range(1,9):
    for i in itertools.combinations(z, j):                     # 取包含j个属性的特征组合
        i=list(i)

        # 交叉验证库，将训练集进行切分交叉验证取平均
        from sklearn import cross_validation
        from sklearn.model_selection import cross_val_score
        knc_kf=KNeighborsClassifier()                          # 定义一个k-邻近分类器
        x =trd[i]                                           
        y =trd["Survived"]
        score=cross_val_score(knc_kf, x, y, cv=5)              # k为5的交叉验证分数列表

        if (score.mean() > temp1 and score.std() < 0.016):     # 特征组合选取条件，在指定标准差范围内，平均分最大
            temp0 = score
            temp1 = score.mean()
            temp2 = score.std()
            dict = {temp1: i}                      # 字典，key为平均分数，value为当前选取的特征组合

c =dict[temp1]   　　　　　　　　　　　　　　          # 最终选取的特征组合，用于建模

# K-邻近算法建模
knc1 = KNeighborsClassifier()  　　　　　　　　　　　 # 定义一个K-邻近分类器
x_trd = trd[c]
y_trd = trd["Survived"]
knc1.fit(x_trd, y_trd)          　　　　　　　　　　　# 训练模型
x_tsd = tsd[c]
y_tsd = knc1.predict(x_tsd)     　　　　　　　　　　　# 进行预测
result = pd.DataFrame({‘PassengerId‘: tsd[‘PassengerId‘].values, ‘Survived‘: y_tsd.astype(np.int32)})  # 预测结果改为要求的格式
result.to_csv("../result/result_knc.csv", index=False)      # 输出结果

　　

　　在提交的结果中k-邻近算法得分相对较高，为0.78947，相应特征组合为["Pclass","Sex","Embarked","Age_mmsc"]。

　　尝试模型融合，方法为在k-邻近算法基础上，用另外几种算法结果进行优化，多次尝试后，得分没有得到提高，不再详述。