Ants 二分图带权最小匹配

Posted 2021-11-22 bhllx

Ants

Solution：

此题最重要的是转化题意！

直接上图（图中红色才是正确方案）：

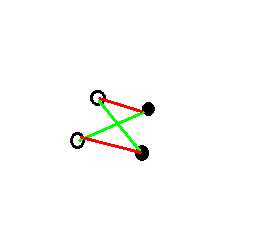
这是一种很简单的情况，但是却告诉了我们很重要的信息。

仔细观察，可以发现，似乎最优方案的两两间连的边，距离值和最小！

那么，找一组连边方案，使得两两距离值和最小必然是最优方案。

为什么会这样呢，

其实是因为只要有相交的边，就会构成类似上图的‘X’型，

那么就必定会存在两个三角形，相交的边一起构成两个三角形中的两边，必然大于其对应的第三边！

因而，我们只要选则第三边，就能保证不交，与此同时，选出来的边距离值和最小。

所以，这就变成了一个裸的二分图带权匹配的问题。

可以用费用流求解，由于此题保证二分图具有完备匹配，所以可以KM。

Code↓：

#include<cmath>
#include<string>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define RG register
#define IL inline
#define LL long long
#define DB double
using namespace std;

IL int gi() {
    char ch=getchar(); RG int x=0,w=0;
    while(ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    return w?-x:x;
}

const int N=110;
const DB eps=1e-6;

DB Min,Max[N],love[N][N],boy[N],girl[N];
int n,ans[N],visboy[N],visgirl[N],match[N];

struct DOT{int x,y;}whi[N],bla[N];

IL DB getdis(DOT A,DOT B) {
    return -sqrt((DB)(A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
}

int getlover(int x) {
    RG int i;
    RG DB dat;
    for (i=1,visgirl[x]=1;i<=n;++i) {
        if (visboy[i]) continue;
        dat=boy[i]+girl[x]-love[x][i];
        if (fabs(dat)<=eps) {
            visboy[i]=1;
            if (!match[i]||getlover(match[i])) {
                match[i]=x;
                return 1;
            }
        }
        else Max[i]=min(Max[i],dat);
    }
    return 0;
}

void KM() {
    memset(boy,0,sizeof(boy));
    memset(girl,0,sizeof(girl));
    memset(match,0,sizeof(match));
    RG int i,j;
    for (i=1;i<=n;++i) {
        girl[i]=love[i][1];
        for (j=2;j<=n;++j)
            girl[i]=max(girl[i],love[i][j]);
    }
    for (i=1;i<=n;++i) {
        memset(Max,67,sizeof(Max));
        while(1) {
            memset(visboy,0,sizeof(visboy));
            memset(visgirl,0,sizeof(visgirl));
            if (getlover(i)) break;
            for (j=1,Min=1e18;j<=n;++j)
                if (!visboy[j]) Min=min(Min,Max[j]);
            for (j=1;j<=n;++j) {
                if (visboy[j]) boy[j]+=Min;
                else Max[j]-=Min;
                if (visgirl[j]) girl[j]-=Min;
            }
        }
    }
    for (i=1;i<=n;++i) ans[match[i]]=i;
    for (i=1;i<=n;++i) printf("%d\\n",ans[i]);   
}

int main()
{
    RG int i,j;
    while (scanf("%d",&n)!=EOF) {
        for (i=1;i<=n;++i) whi[i].x=gi(),whi[i].y=gi();
        for (i=1;i<=n;++i) bla[i].x=gi(),bla[i].y=gi();
        for (i=1;i<=n;++i)
            for (j=1;j<=n;++j) love[i][j]=getdis(whi[i],bla[j]);
        KM();
    }
    return 0;
}

The End