打印杨辉三角形(Pascal's triangle)——利用队列

Posted 2020-07-17 Cainv89

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了打印杨辉三角形(Pascal's triangle)——利用队列相关的知识，希望对你有一定的参考价值。

打印杨辉三角形(Pascal’s triangle)——利用链式队列

1. 杨辉三角的概念

杨辉三角，又称贾宪三角形，帕斯卡三角形，是二项式系数在三角形中的一种几何排列。
将二项式 $(a+b)^i$ 展开，其系数构成杨辉三角形(国外称Pascal’s triangle)，按行将展开式系数的前n行打印出来。从三角形的形状可知，除第1行以外，在打印第i行时，用到上一行(第i-1行)的数据，在打印第i+1行时，又用到第i行的数据。
注：在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623—-1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。

2. 杨辉三角的基本性质

前提是端点的数为1。
每个数等于它上方两数之和。
每行数字左右对称，由1开始逐渐变大。
第n行的数字有n+1项。
第n行数字和为 $2^{n-1}$ 。
第n行的m个数可表示为 C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
第n行的第m个数和第n-m+1个数相等，为组合数性质之一。
每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
$(a+b)^n$ 的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
将各行数字相排列，可得 $11^{n-1}$ (n为行数)：1= $11^0$ ; 11= $11^1$ ; 121= $11^2$ ……当n>5时会不符合这一条性质，此时应把第n行的最右面的数字“1”放在个位，然后把左面的一个数字的个位对齐到十位，以此类推，把空位用“0”补齐，然后把所有的数加起来，得到的数正好是 $11^{n-1}$ 。以n=11为例，第十一行的数为：1,10,45,120,210,252,210,120,45,10,1，结果为 25937424601=1110。

3. 打印杨辉三角形的算法原理

第i行元素与第i+1行元素的关系示意图：
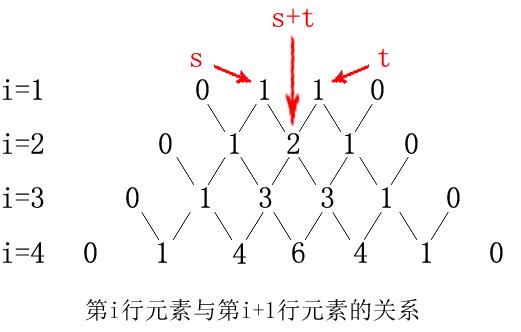
从第i行的数据出队并计算出第i+1行的数据入队的示意图：

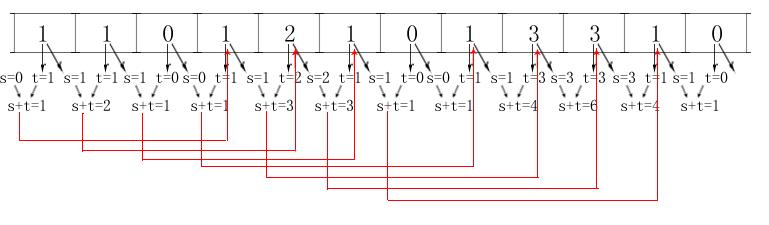
4. 利用队列实现逐行打印杨辉三角形的前n行

4.1 链表结点结构的定义

文件：LinkNode.h


#ifndef LINK_NODE_H_


#define LINK_NODE_H_



#include <iostream>


#include <string>


#include <strstream>


using namespace std;

template <class T>
struct LinkNode         //链表结点类的定义
{
    T data;             //数据域
    LinkNode<T> *link;  //指针域——后继指针
    //仅初始化指针成员的构造函数
    LinkNode(LinkNode<T>* ptr = NULL){ link = ptr; }
    //初始化数据与指针成员的构造函数
    LinkNode(const T& value, LinkNode<T>* ptr = NULL){ data = value; link = ptr; }
};


#endif /* LINK_NODE_H_ */

4.2 链式队列的类定义及其操作的实现

文件：LinkedQueue.h


#ifndef LINKED_QUEUE_H_


#define LINKED_QUEUE_H_



#include "LinkNode.h"


#include "Queue.h"


template <class T>
class LinkedQueue : public Queue<T>
{
public:
    LinkedQueue();                      //构造函数
    virtual ~LinkedQueue();             //析构函数
public:
    virtual bool getHead(T& x) const;       //读取队头元素，并将该元素的值保存至x
    virtual bool EnQueue(const T& x);       //新元素x入队
    virtual bool DeQueue(T& x);             //队头元素出队，并将该元素的值保存至x    
    virtual bool IsEmpty() const;           //判断队列是否为空
    virtual bool IsFull() const;            //判断队列是否为满
    virtual void MakeEmpty();               //清空队列的内容
    virtual int getSize() const;            //计算队列中元素个数
public:
    template <class T>
    friend ostream& operator<<(ostream& os, const LinkedQueue<T>& q);   //输出队列中元素的重载操作<<
private:
    LinkNode<T> *front; //队头指针，即链头指针
    LinkNode<T> *rear;  //队尾指针，即链尾指针
};

//构造函数
template <class T>
LinkedQueue<T>::LinkedQueue()
    : front(NULL), rear(NULL)
{
    cout << "$ 执行构造函数" << endl;
}

//析构函数
template <class T>
LinkedQueue<T>::~LinkedQueue()
{
    cout << "$ 执行析构函数" << endl;
    MakeEmpty();
}

//读取队头元素，并将该元素的值保存至x
template <class T>
bool LinkedQueue<T>::getHead(T& x) const
{
    if (true == IsEmpty())
    {
        return false;
    }
    x = front->data;
    return true;
}

//新元素x入队
template <class T>
bool LinkedQueue<T>::EnQueue(const T& x)
{
    LinkNode<T> *newNode = new LinkNode<T>(x);
    if (NULL == newNode)
    {
        return false;
    }

    if (NULL == front)
    {
        front = newNode;
        rear = newNode;
    }
    else
    {
        rear->link = newNode;
        rear = rear->link;
    }
    return true;
}

//队头元素出队，并将该元素的值保存至x
template <class T>
bool LinkedQueue<T>::DeQueue(T& x)
{
    if (true == IsEmpty())
    {
        return false;
    }
    LinkNode<T> *curNode = front;
    front = front->link;
    x = curNode->data;
    delete curNode;
    return true;
}

//判断队列是否为空
template <class T>
bool LinkedQueue<T>::IsEmpty() const
{
    return (NULL == front) ? true : false;
}

//判断队列是否为满
template <class T>
bool LinkedQueue<T>::IsFull() const
{
    return false;
}

//清空队列的内容
template <class T>
void LinkedQueue<T>::MakeEmpty()
{
    LinkNode<T> *curNode = NULL;
    while (NULL != front)           //当链表不为空时，删去链表中所有结点
    {
        curNode = front;            //保存被删结点
        front = curNode->link;      //被删结点的下一个结点成为头结点
        delete curNode;             //从链表上摘下被删结点
    }
}

//计算队列中元素个数
template <class T>
int LinkedQueue<T>::getSize() const
{
    int count = 0;
    LinkNode<T> *curNode = front;
    while (NULL != curNode)
    {
        curNode = curNode->link;
        count++;
    }
    return count;
}

//输出队列中元素的重载操作<<
template <class T>
ostream& operator<<(ostream& os, const LinkedQueue<T>& q)
{
    int i = 0;
    LinkNode<T> *curNode = q.front;
    while (NULL != curNode)
    {
        os << "[" << i++ << "]" << " : " << curNode->data << endl;
        curNode = curNode->link;
    }
    return os;
}


#endif /* LINKED_QUEUE_H_ */

4.3 利用队列实现逐行打印杨辉三角形的前n行的算法实现

文件：YANGVI.h


#ifndef YANGVI_H_


#define YANGVI_H_



#include "LinkedQueue.h"


void set_space(int count, int i)
{
    cout << endl;
    while (i <= count + 1)
    {
        cout << "   ";
        i++;
    }
}

template <class T>
void YANGVI(LinkedQueue<T>* linkedQueue, int n)
{
    //分行打印二项式(a+b)^n展开式的系数。
    //在程序中利用了一个队列，在输出上一行系数时，将其下一行的系数预先放入队列中，在各行系数之间插入一个0。
    cout << "=> 打印杨辉三角形，行数n = " << n << endl;
    int i = 1;
    int s = 0;
    int k = 0;
    int t = 0;
    linkedQueue->EnQueue(i);
    linkedQueue->EnQueue(i);
    for (i = 1; i <= n; i++)
    {
        set_space(n, i);
        linkedQueue->EnQueue(k);
        for (int j = 1; j <= i + 2; j++)
        {
            linkedQueue->DeQueue(t);
            linkedQueue->EnQueue(s + t);
            s = t;
            if (j != i + 2)
            {
                cout << s << "    ";
            }
        }
    }
    cout << endl;
}


#endif /* YANGVI_H_ */

4.4 主函数(main函数)的实现

文件：main.cpp


#include "YANGVI.h"


//判断输入的字符串每个字符是否都是数值0~9
bool IsNumber(const string& s_num)
{
    for (size_t i = 0; i < s_num.size(); i++)
    {
        if ((s_num[i] < '0') || (s_num[i] > '9'))
        {
            return false;
        }
    }
    return true;
}

//输入行数n
int get_n()
{
    cout << "> 输入行数，n = ";
    string s_n;
    cin >> s_n;
    while (false == IsNumber(s_n))
    {
        cout << "* 输入有误，请重新输入：";
        cin >> s_n;
    }
    return atoi(s_n.c_str());
}

//构造链式队列
template <class T>
LinkedQueue<T>* construct_linkedqueue()
{
    cout << "\\n==> 创建链式队列" << endl;
    LinkedQueue<T> *linkedQueue = new LinkedQueue<T>;
    return linkedQueue;
}

//析构链式队列
template <class T>
void destory_linkedqueue(LinkedQueue<T>* linkedQueue)
{
    cout << "\\n==> 释放链式队列在堆中申请的空间，并将指向该空间的指针变量置为空" << endl;
    delete linkedQueue;
    linkedQueue = NULL;
}

int main(int argc, char* argv[])
{
    LinkedQueue<int> *linkedQueue = construct_linkedqueue<int>();
    int n = get_n();
    YANGVI(linkedQueue, n);
    destory_linkedqueue(linkedQueue);
    system("pause");
    return 0;
}

4.5 杨辉三角形打印结果

控制台输出，当杨辉三角形行数n=6的情况。

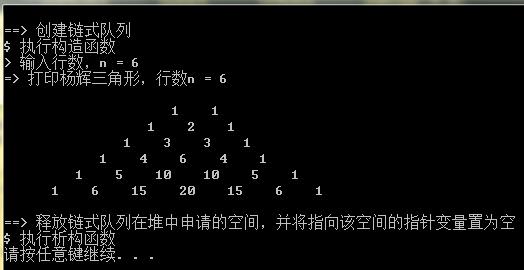
参考文献：
[1]《数据结构(用面向对象方法与C++语言描述)(第2版)》殷人昆——第三章
[2] 百度搜索关键字：杨辉三角

以上是关于打印杨辉三角形(Pascal's triangle)——利用队列的主要内容，如果未能解决你的问题，请参考以下文章

算法：杨辉三角（Pascal's Triangle）

[LeetCode] 118. Pascal's Triangle 杨辉三角

杨辉三角形

LeetCode118 Pascal's Triangle

杨辉三角形递归与非递归

119 Pascal's Triangle II 帕斯卡三角形 II Pascal's Triangle II