数据结构之树篇3——平衡二叉树（AVL树）

Posted 2020-11-30 czc1999

引入

上一篇写了二叉排序树，构建一个二叉排序树，如果构建序列是完全有序的，则会出现这样的情况：

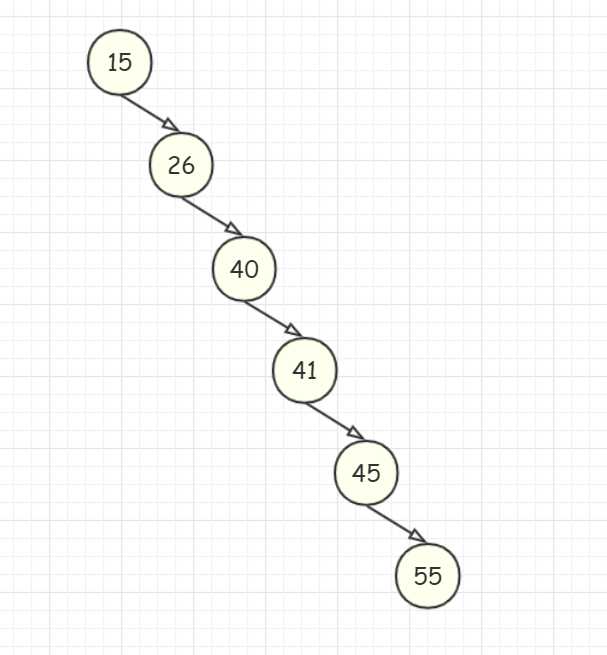
显然这种情况会使得二叉搜索树退化成链表。当出现这样的情况，二叉排序树的查找也就退化成了线性查找，所以我们需要合理调整二叉排序树的形态，使得树上的每个结点都尽量有两个子结点，这样整个二叉树的高度就会大约在(log(n)) 左右，其中 (n) 为结点个数。

基本性质

? AVL树也称为平衡二叉树，是一种自平衡的二叉排序树，本质上仍然是一颗二叉排序树，只是增加了“平衡”的要求，平衡是指，对AVL树中任何节点的两个子树的高度之差（称为平衡因子）的绝对值不超过 (1) 。能保证上面这一点，AVL树的高度就能始终保持在 (O(logn)) 级别。

数据结构定义

由于需要对每个结点都得到平衡因子，因此在AVL树的结构中加入一个变量height，用来记录当前结点为根结点的子树的高度：

typedef struct Node
{
    char data;
    int height;
    struct Node* Left;
    struct Node* Right;
}*AVLTree;

获取 root 结点高度：

int getHeight(Node *root){
    if(!root) return 0;//空节点高度为0
    return root->height;
}

基本操作

查找

? AVL树是一颗二叉查找树，因此查找操作与二叉查找树相同。因为AVL树的高度为 (O(logn)) 级别，所以查找操作的时间复杂度为 (O(logn))。

可以得到和二叉查找树完全相同的代码：

//找不到返回NULL，找到返回该节点。
//非递归
Node* Find(AVLTree t, int x) {
    if (!t)return NULL;
    if (t->data == x) return t;
    if (x < t->data) return BSTreeFind(t->Left, x);
    if (x > t->data) return BSTreeFind(t->Right, x);
}
//非递归
Node* Find(AVLTree T,int x) {
    BSTree p = T;
    while (p) {
        if (x == p->data)
            return p;
        p = x > p->data ? p->Right : p->Left;
    }
    return NULL;
}

插入

左旋

先抛开AVL树的插入问题，看下面左边的二叉排序树。大家本来和平共处，突然有一天 B 觉得自己的权值比 A 大，要造反，但是B要做根结点，必须也要保证调整后的树仍然是一颗二叉排序树。

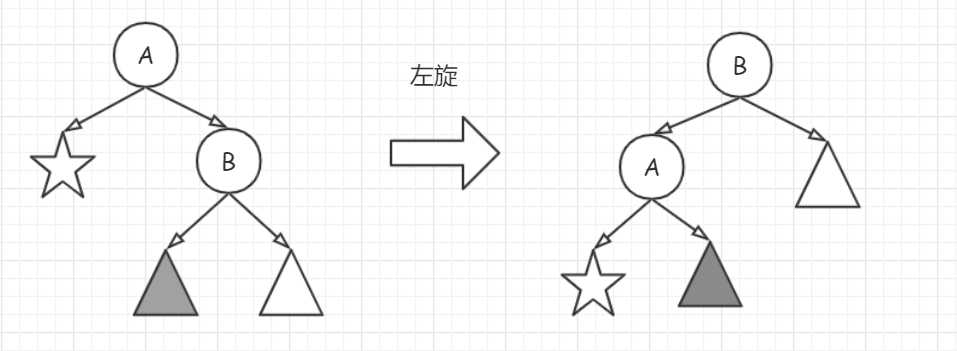
☆上所有权值都比A小， ? 上所有权值都比B大，无需在调整中进行位置变动；因为调整后B的左孩子变成了A，那么▲必须移动到其他地方去，因为A、B、▲的权值关系满足 A<▲<B ，所以让▲成为A的右子树即可。

这个调整过程称为左旋，分解调整过程如下：

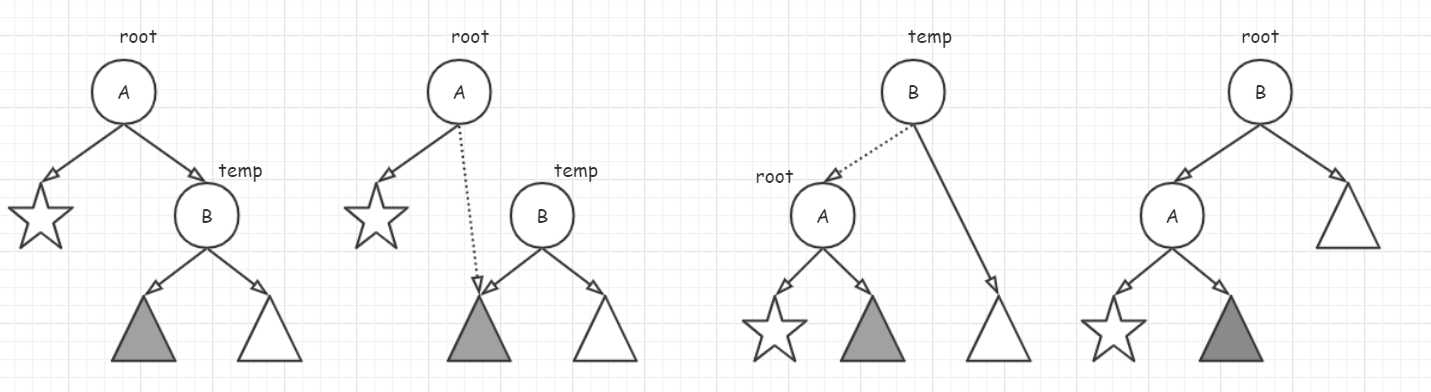
代码如下：

void L(AVLTree *root){
    Node* temp = (*root)->Right; //root指向结点A，temp指向结点B
    (*root)->Right = temp->Left; //图示步骤2
    temp->Left = *root; //图示步骤3
    root->height = max(getHeight(root->Left), getHeight(root->Rihgt)) + 1;//更新结点A高度
    temp = max(getHeight(temp->Left), getHeight(temp->Rihgt)) + 1;//更新结点B高度
    *root = temp;//图示步骤4
}

右旋

右旋是左旋的逆过程，如下：

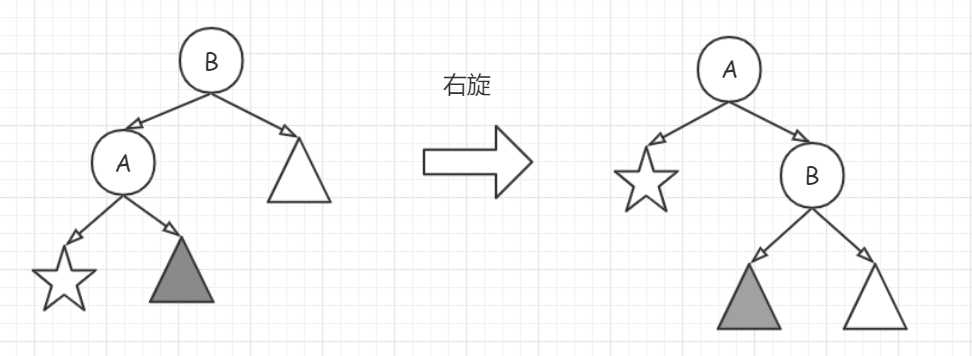
分解调整过程如下：

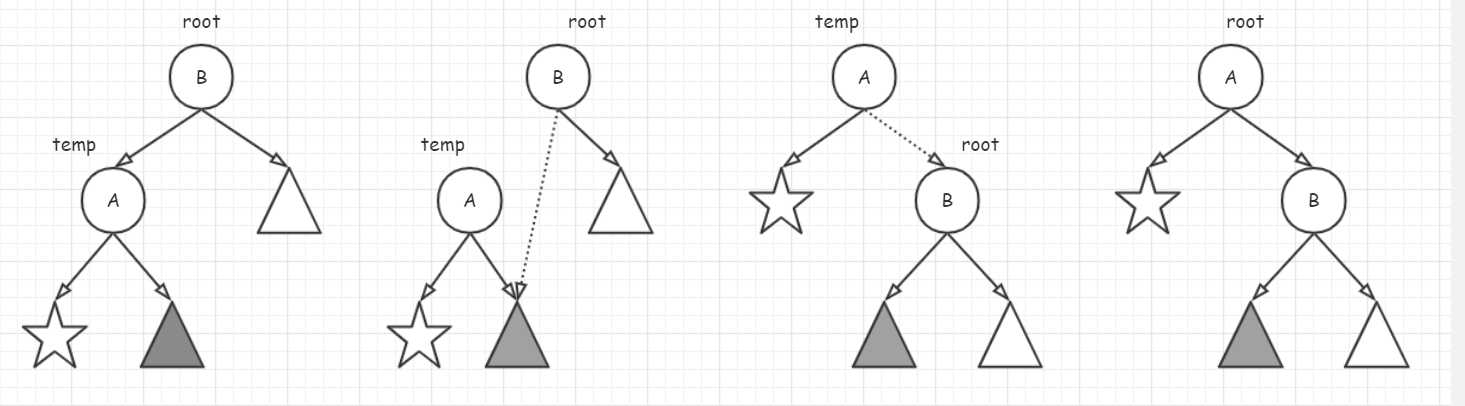
代码如下：

void R(AVLTree *root) {
    Node* temp = (*root)->Left;//root指向结点B，temp指向结点A
    (*root)->Left = temp->Right;
    temp->Right = *root;
    root->height = max(getHeight(root->Left), getHeight(root->Rihgt)) + 1;
    temp = max(getHeight(temp->Left), getHeight(temp->Rihgt)) + 1;
    *root = temp;
}

? 接下来讨论AVL树的插入操作，假设现在已经有一颗平衡二叉树，那么在向其中插入一个结点时，一定会有结点的平衡因子发生改变，此时就可能会有结点的平衡因子大于1 ，这样以该结点为根结点的子树就是失去平衡的，会使平衡二叉树发生失衡的情况可以分为下面四种：

LL、RR型

左左（LL）、右右（RR），LL，RR只表示树型（导致树失去平衡的插入位置），不是左旋、右旋的意思。

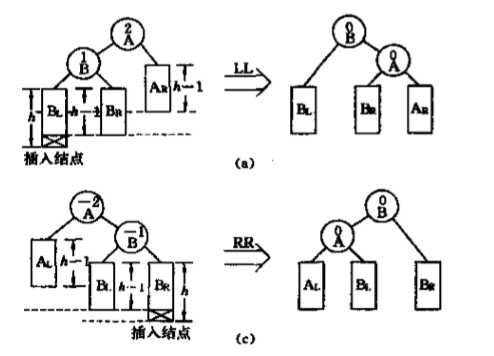
对于LL型，需要以A结点为根进行右旋；

对于RR型，需要以A为根结点进行左旋。

所以代码如下：

void RR_Rotate(AVLTree *root){
    L(root);
}

void LL_Rotate(AVLTree *root) {
    R(root);
}

LR，RL型

左右（LR）、右左（RL）。

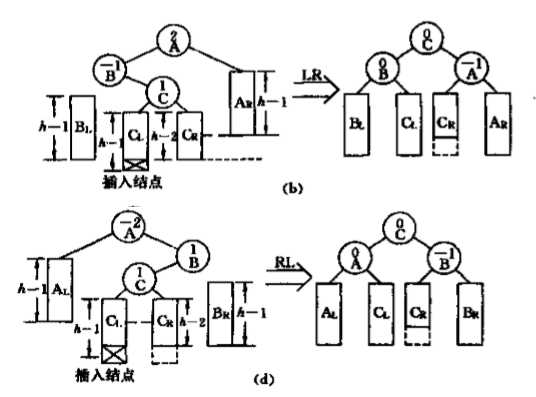
对于LR型，需要先以B结点为根结点进行一次左旋，再以A结点为根结点进行一次右旋。

对于RL型，需要先以B结点为根结点进行一次右旋，再以A结点为根结点进行一次左旋。

void LR_Rotate(AVLTree *root) {
    L(&(*root)->Left);
    R(root);
}
void RL_Rotate(AVLTree *root) {
    R(&(*root)->Right);
    L(root);
}

插入结点

插入算法就是出现不平衡状态时，判断需要使用哪种旋转方式来使得二叉树保持平衡

AVLTree InsertAVLTree(AVLTree root, int x) {
    if (root == NULL) {
        root = new Node;
        root->Left = NULL;
        root->Right = NULL;
        root->data = x;
        return root;
    }
    if (x > root->data) { 
            //递归返回插入位置的父节点或者祖父……。
            root->Right = InsertAVLTree(root->Right, x); 
            //如果插入之后失去了平衡
            if (height(root->Left) - height(root->Right) == -2) {
                //如果插入的值大于,当前节点的左孩子节点，说明该节点是插在root的右子树上的
                if (x > root->Left->data) RR_Rotate(&root);
                else RL_Rotate(&root);
            }
    }

    else if (x < root->data) {
        root->Left = InsertAVLTree(root->Left, x);
        if (height(root->Left) - height(root->Right) == 2) {
            if (x < root->Left->data) LL_Rotate(&root);
            else LR_Rotate(&root);
        }
    }
    else { 
        cout << "the number is already included." << endl;
        return NULL; 
    }
    return root;
}

删除结点

和二叉排序树的节点的删除差不多，就是多出来一个判断从哪个子树删除节点的问题。

void AVLTreeDel(AVLTree *root, int data)
{
    if (!*root) {
        cout << "delete failed" << endl;
        return;
    }
    Node *p = *root;  
    if (data == p->data) {
        //左右子树都非空  
        if (p->Left && p->Right) {
            //在高度更大的那个子树上进行删除操作
            //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
            if (height(p->Left) > height(p->Right)) {
                Node *pre=NULL,*q = p->Left;
                if (!q->Right)
                    q->Right = p->Right;
                else {
                    while (q->Right) {
                        pre = q;
                        q = q->Right;
                    }
                    pre->Right = q->Left;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root = q;
            }
            else {
                Node *pre = NULL, *q = p->Right;
                if (!q->Left)
                    q->Left = p->Left;
                else {
                    while (q->Left) {
                        pre = q;
                        q = q->Left;
                    }
                    pre->Left = q->Right;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root=q;
            }
        }
        else 
            (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
        delete p;
    }
    else if (data < p->data){//要删除的节点在左子树中  
        //在左子树中进行递归删除  
        AVLTreeDel(&(*root)->Left, data);
        //判断是否仍然满足平衡条件  
        if (height(p->Right) - height(p->Left) == 2){
            //如果当前节点右孩子的左子树更高
            if (height(p->Right->Left) > height(p->Right->Right))
                RL_Rotate(root);
            else  
                RR_Rotate(root);
        }
    }
    else{
        AVLTreeDel(&(*root)->Right, data);
        if (height(p->Left) - height(p->Right) == 2) {
            if (height((*root)->Left->Left) > height((*root)->Left->Right))
                LL_Rotate(root);
            else
                LR_Rotate(root);
        }
    }
}

完整测试代码：

#pragma once
#include "top.h"

typedef BTreeNode Node, *AVLTree;

void RR_Rotate(AVLTree *root){
    Node* Right = (*root)->Right;
    (*root)->Right = Right->Left;
    Right->Left = *root;
    *root = Right;
}

void LL_Rotate(AVLTree *root) {
    Node* Left = (*root)->Left;
    (*root)->Left = Left->Right;
    Left->Right = *root;
    *root = Left;
}
void LR_Rotate(AVLTree *root) {
    RR_Rotate(&(*root)->Left);
    return LL_Rotate(root);
}
void RL_Rotate(AVLTree *root) {
    LL_Rotate(&(*root)->Right);
    RR_Rotate(root);
}
AVLTree AVLTreeInsert(AVLTree root, int x) {
    if (root == NULL) {
        root = new Node;
        root->Left = NULL;
        root->Right = NULL;
        root->data = x;
        return root;
    }
    if (x > root->data) { 
            root->Right = AVLTreeInsert(root->Right, x); 
            //递归返回插入位置的父节点或者祖父……，如果失去了平衡
            if (height(root->Left) - height(root->Right) == -2) {
            //如果插入的值大于,当前节点的右孩子节点，说明该节点是插在root的右子树上的
                //if (x > root->Left->data) RR_Rotate(&root);不能保证该节点一定有左子树
                if (x > root->Right->data)RR_Rotate(&root);
                else RL_Rotate(&root);
            }
    }
    else if (x < root->data) {
        root->Left = AVLTreeInsert(root->Left, x);
        if (height(root->Left) - height(root->Right) == 2) {
            if (x < root->Left->data) LL_Rotate(&root);
            else LR_Rotate(&root);
        }
    }
    else { 
        cout << "the number is already included." << endl;
        return NULL; 
    }
    return root;
}

AVLTree AVLTreeCreat(int *a, int length) {
    AVLTree T = NULL;
    for (int i = 0; i < length; i++) {
        T = AVLTreeInsert(T, a[i]);
    }
    return T;
}
Node* AVLFind(AVLTree T, int x) {
    Node *p = T;
    while (p) {
        if (x == p->data) break;
        p = x > p->data ? p->Right : p->Left;
    }
    return p;
}

AVLTree AVLMax(AVLTree p)
{
    if (!p) return NULL;
    if (p->Right == NULL)
        return p;
    return AVLMax(p->Right);
}

AVLTree AVLMin(AVLTree p)
{
    if (!p)
        return NULL;
    if (p->Left == NULL)
        return p;
    return AVLMin(p->Left);
}

void AVLTreeDel(AVLTree *root, int data)
{
    if (!*root) {
        cout << "delete failed" << endl;
        return;
    }
    Node *p = *root;  
    if (data == p->data) {
        //左右子树都非空  
        if (p->Left && p->Right) {
            //在高度更大的那个子树上进行删除操作
            //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
            if (height(p->Left) > height(p->Right)) {
                Node *pre=NULL,*q = p->Left;
                if (!q->Right)
                    q->Right = p->Right;
                else {
                    while (q->Right) {
                        pre = q;
                        q = q->Right;
                    }
                    pre->Right = q->Left;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root = q;
            }
            else {
                Node *pre = NULL, *q = p->Right;
                if (!q->Left)
                    q->Left = p->Left;
                else {
                    while (q->Left) {
                        pre = q;
                        q = q->Left;
                    }
                    pre->Left = q->Right;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root=q;
            }
        }
        else 
            (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
        delete p;
    }
    else if (data < p->data){//要删除的节点在左子树中  
        //在左子树中进行递归删除  
        AVLTreeDel(&(*root)->Left, data);
        //判断是否仍然满足平衡条件  
        if (height(p->Right) - height(p->Left) == 2){
            //如果当前节点右孩子的左子树更高
            if (height(p->Right->Left) > height(p->Right->Right))
                RL_Rotate(root);
            else  
                RR_Rotate(root);
        }
    }
    else{
        AVLTreeDel(&(*root)->Right, data);
        if (height(p->Left) - height(p->Right) == 2) {
            if (height((*root)->Left->Left) > height((*root)->Left->Right))
                LL_Rotate(root);
            else
                LR_Rotate(root);
        }
    }
}

int height(BTree L) {
    if (L == NULL)
        return 0;
    int left = height(L->Left);
    int right = height(L->Right);
    return left >= right ? left + 1 : right + 1;
}

void checkCreat() {
    int length = 10;
    int *a = getNoRepateRandomArray(length, 10);

    for (int i = 0; i < length; i++) {
        cout << a[i] << ",";
    }
        
    cout << endl;
    AVLTree T = AVLTreeCreat(a, length);
    int t = rand() % length;
    AVLTreeDel(&T, a[t]);
    for (int i = t; i < length - 1; i++) {
        a[i] = a[i + 1];
    }
    
    Preorder(T);
    cout << endl;
    Inorder(T);
    cout << endl;
    Postorder(T);
    cout << endl;
    free(a);
}