数据结构与算法:树 AVL平衡二叉排序树
Posted 史大拿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法:树 AVL平衡二叉排序树相关的知识,希望对你有一定的参考价值。
Tips: 采用java语言,关注博主,底部附有完整代码
工具:IDEA
本系列介绍的是数据结构: 树
这是第九篇目前计划一共有11篇:
- 二叉树入门
- 顺序二叉树
- 线索化二叉树
- 堆排序
- 赫夫曼树(一)
- 赫夫曼树(二)
- 赫夫曼树(三)
- 二叉排序树(BST)
- 平衡二叉排序树AVL本篇
- 2-3树,2-3-4树,B树 B+树 B*树 了解
- 数据结构与算法:树 红黑树 (十一)
敬请期待吧~~
高光时刻:
添加情况分析:
| 情况一(左旋) | 情况二(右旋) | 情况三(左旋 右旋) | 情况四(右旋 左旋) |
|---|---|---|---|
 |  |  |  |
删除情况分析:
| 情况一(右旋) | 情况二(左旋) | 情况三(右旋左旋 ) | 情况四(左旋 右旋) |
|---|---|---|---|
 |  |  |  |
基本介绍
在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树
特点:
- AVL树首先是一颗二叉排序树(BST)
- 根节点左子树高度和右子树高度相差高度最大为1
- 每一个左子树和右子树也都是AVL树
- AVL树的结构一定是‘扁平的’
一张图搞懂:
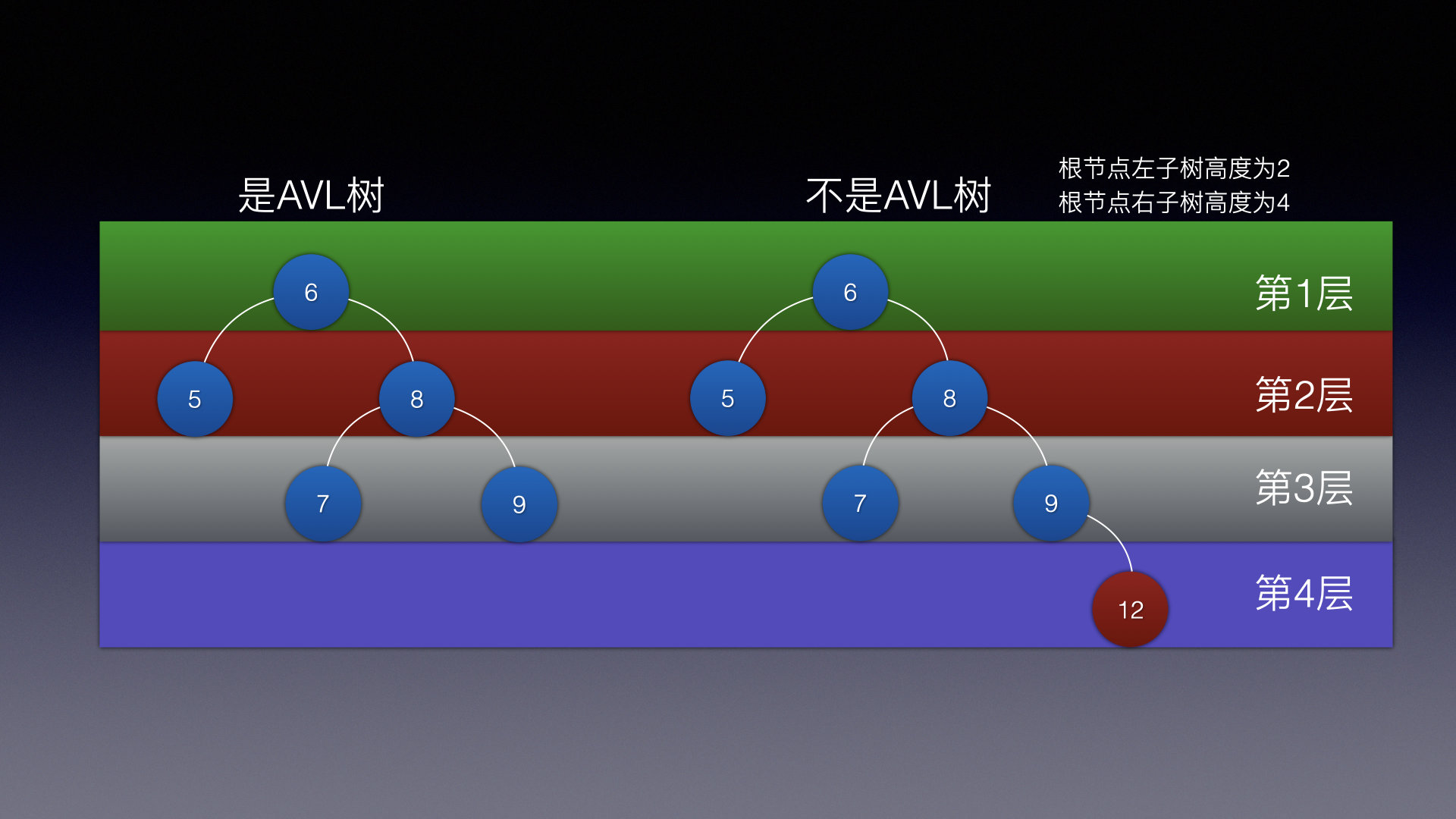
定义结点类
public class AVLNode
int value;
// 左子结点
AVLNode leftNode;
// 右子结点
AVLNode rightNode;
public AVLNode(int value)
this.value = value;
@Override
public String toString()
return "SortTreeNode" +
"value=" + value +
'';
// 搜索当前结点
// @param return: [null 不存在]
public AVLNode search(int value)
.....
// 搜索当前结点的父结点
public AVLNode searchParent(int value)
..........
// 中序遍历
public void show()
...
这里隐藏了三个方法
- 搜索当前结点
- 搜索当前结点的父结点
- 中序遍历
是因为上一篇:二叉排序树(BST)已经说过了,就不重复介绍了,代码很简单,有需要的话翻过去看看吧~
添加结点
public void add(AVLNode node)
if (node == null)
return;
// 如果传入的结点 <= 当前结点
// 说明当前结点应该存放在左子结点上
if (node.value <= value)
// 如果左子结点为null 说明是叶子结点 直接存放即可
if (leftNode == null)
leftNode = node;
else
leftNode.add(node);
// 如果传入的结点 >= 当前结点
// 说明当前结点应该存放在右子结点上
if (node.value >= value)
// 如果左子结点为null 说明是叶子结点 直接存放即可
if (rightNode == null)
rightNode = node;
else
rightNode.add(node);
/// .... 旋转......
添加结点和上一篇讲的也一模一样
但是如果真这样写,那不就成了BST树了么,先来分析情况,然后再看代码
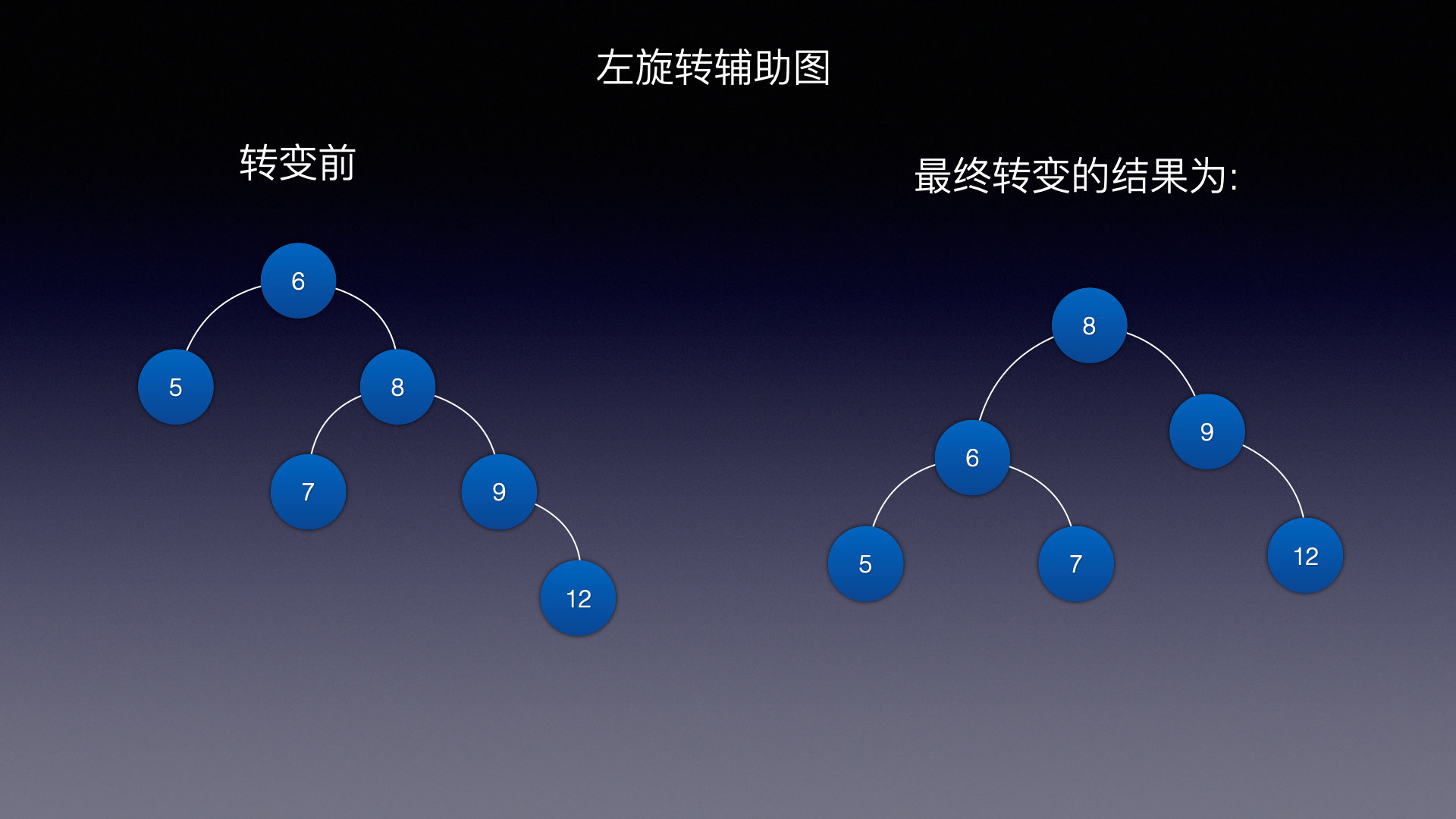
情况一 (左旋)
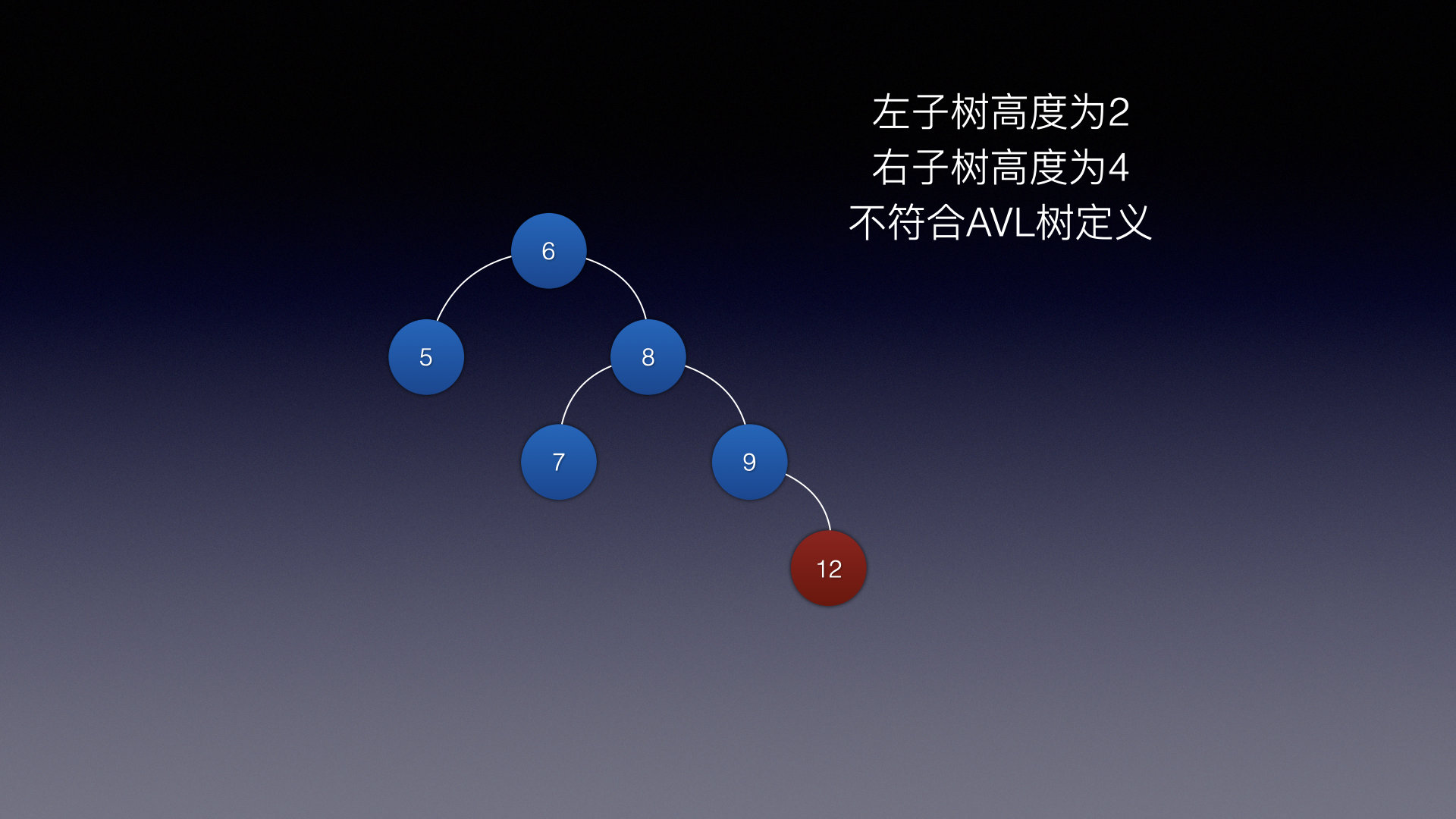
假设当前树结构是这样的,在没添加12之前,这是一颗AVL树
但是一旦添加了12就不满足AVL树的特性了
因为右子树高度 - 左子树高度 = 2 ,说明已经不平衡了
那么就以root结点为“支点” 向左旋转一下
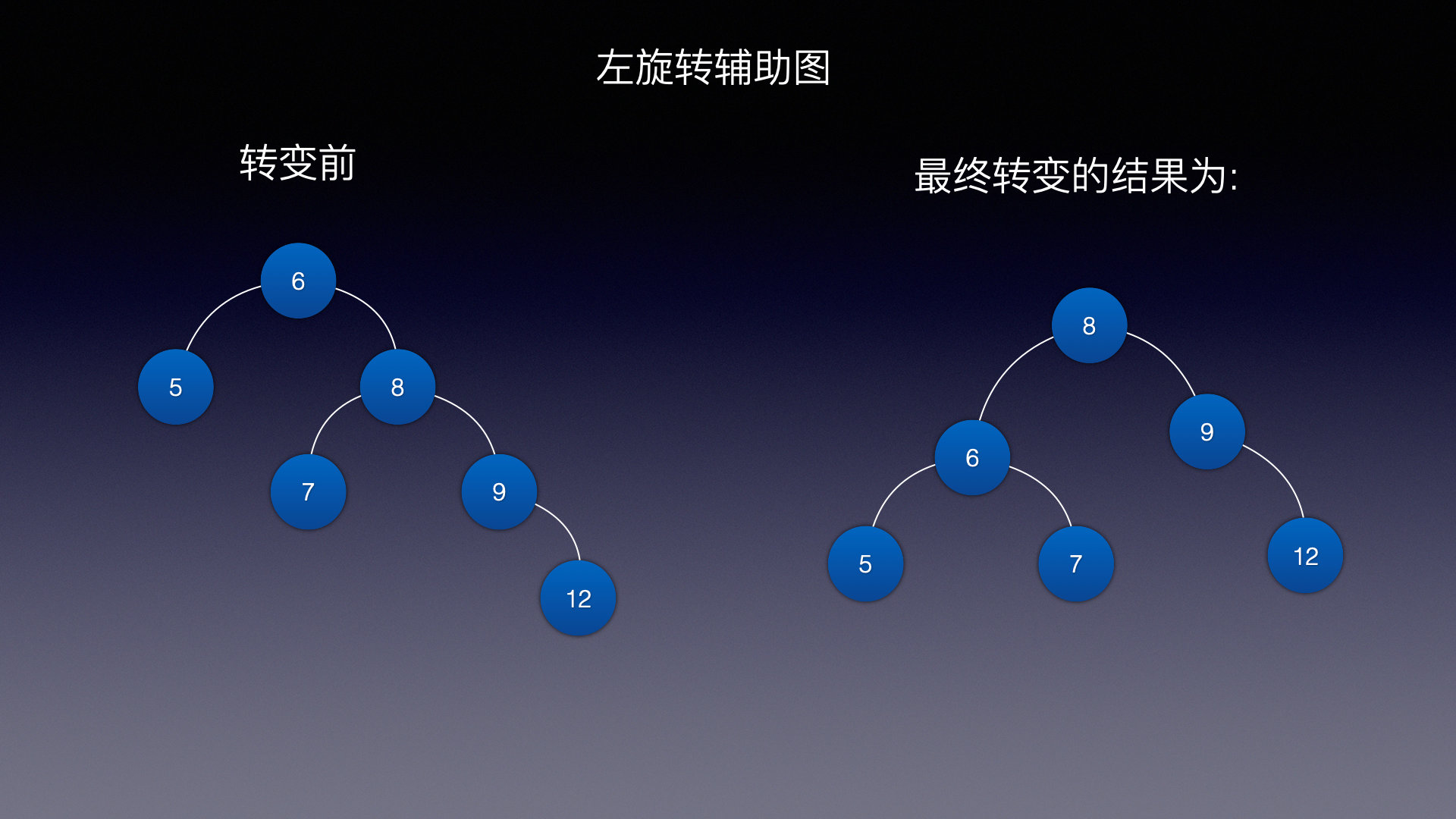
转变前中序遍历结果为: 5, 6, 7, 8, 9, 12
转变后的中序结果为: 5, 6, 7, 8, 9, 12
说明是成功的!
那么问题就来了,如何左旋?

这张图很重要一定要多看几遍,左旋搞不懂,AVL树就不用看了!!
这里支点 是根节点
左旋是将支点的右子结点指向 支点的右子结点的左子结点
支点的右子结点 指向 支点
这几个字分开都认识,合在一起好像是有点晕,直接看完整流程图!
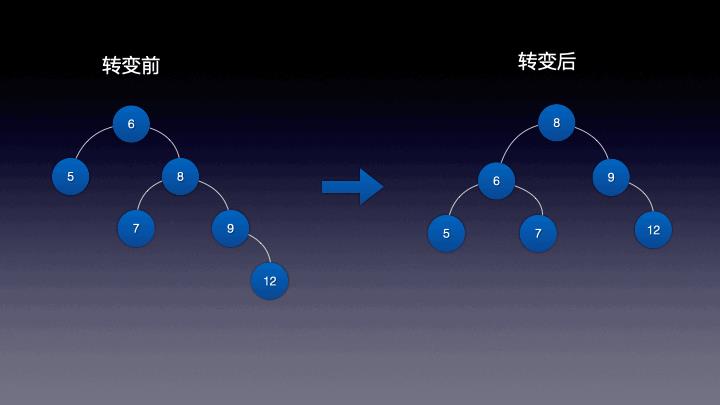
一共拆分成了6步:
- 创建一个新结点,和root结点相同
- 将原本left结点赋值到新结点左子结点上
- 将原本右结点的左结点,赋值到新结点的右结点上
- 将根节点转变为 右结点
- 将根节点右结点赋值为右结点的右结点
- 将新结点赋值到左结点上
来看一眼代码:
# AVLNode.java
// 左旋
public void leftRotate()
// 1. 创建一个新结点 和 root结点相同
AVLNode newNode = new AVLNode(value);
// 2. 将原本left结点赋值到新结点上
newNode.leftNode = leftNode;
// 3. 将原本右结点的左结点 赋值到新结点的右结点上
newNode.rightNode = rightNode.leftNode;
// 4. 将根节点转变为右结点
value = rightNode.value;
// 5. 将根节点右结点赋值为右结点的右结点
// 此时根节点就转变了!
rightNode = rightNode.rightNode;
// 6. 将新结点复制到左结点上
leftNode = newNode;
那么知道了左旋,代码应该怎么写呢?
现在已知条件是 右子树高度 - 左子树高度 >= 2 需要左旋
那么树的高度怎么计算呢?
# AVLNode.java
// 获取树的高度
public int height()
int leftH = leftNode == null ? 0 : leftNode.height();
int rightH = rightNode == null ? 0 : rightNode.height();
return Math.max(leftH, rightH) + 1;
// 左子树高度
public int leftHeight()
return leftNode == null ? 0 : leftNode.height();
// 右子树高度
public int rightHeight()
return rightNode == null ? 0 : rightNode.height();
这里要注意,不是什么树都能获取树的高度的!
这里是通过递归获取到树的高度,这里能使用递归完全是因为是AVL树,AVL树的结构一定是扁平的,
这里细品一下!
获取到了树的高度,那么直接旋转即可
public void add(AVLNode node)
if (node == null)
return;
....
// 添加结点
// 右子树高度 - 左子树高度 >= 2 说明需要 '左旋转'
if ( rightHeight() - leftHeight() >= 2)
leftRotate();
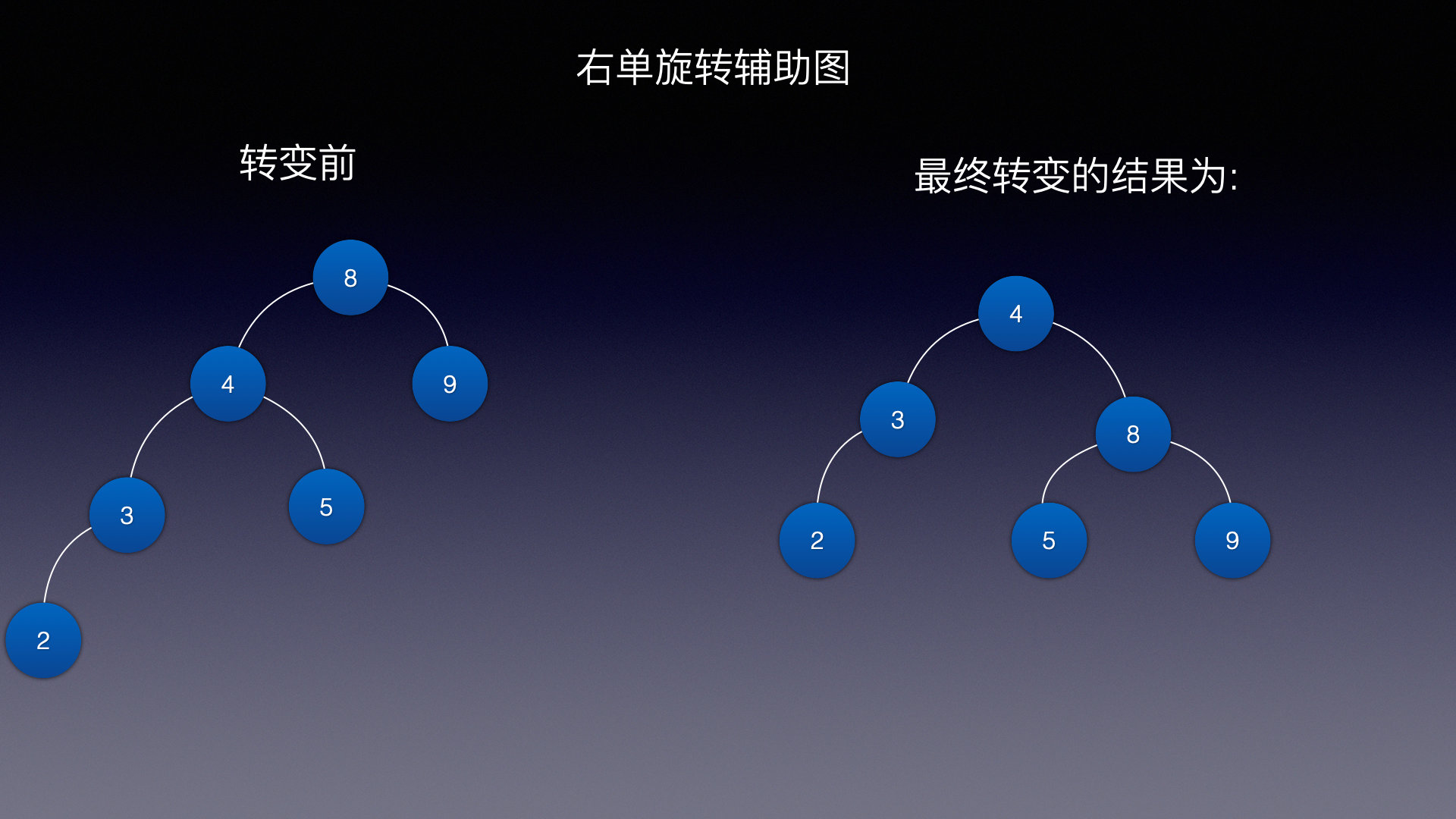
情况二 (右旋)
右旋和左旋道理一样,来看一张图什么情况下需要右旋
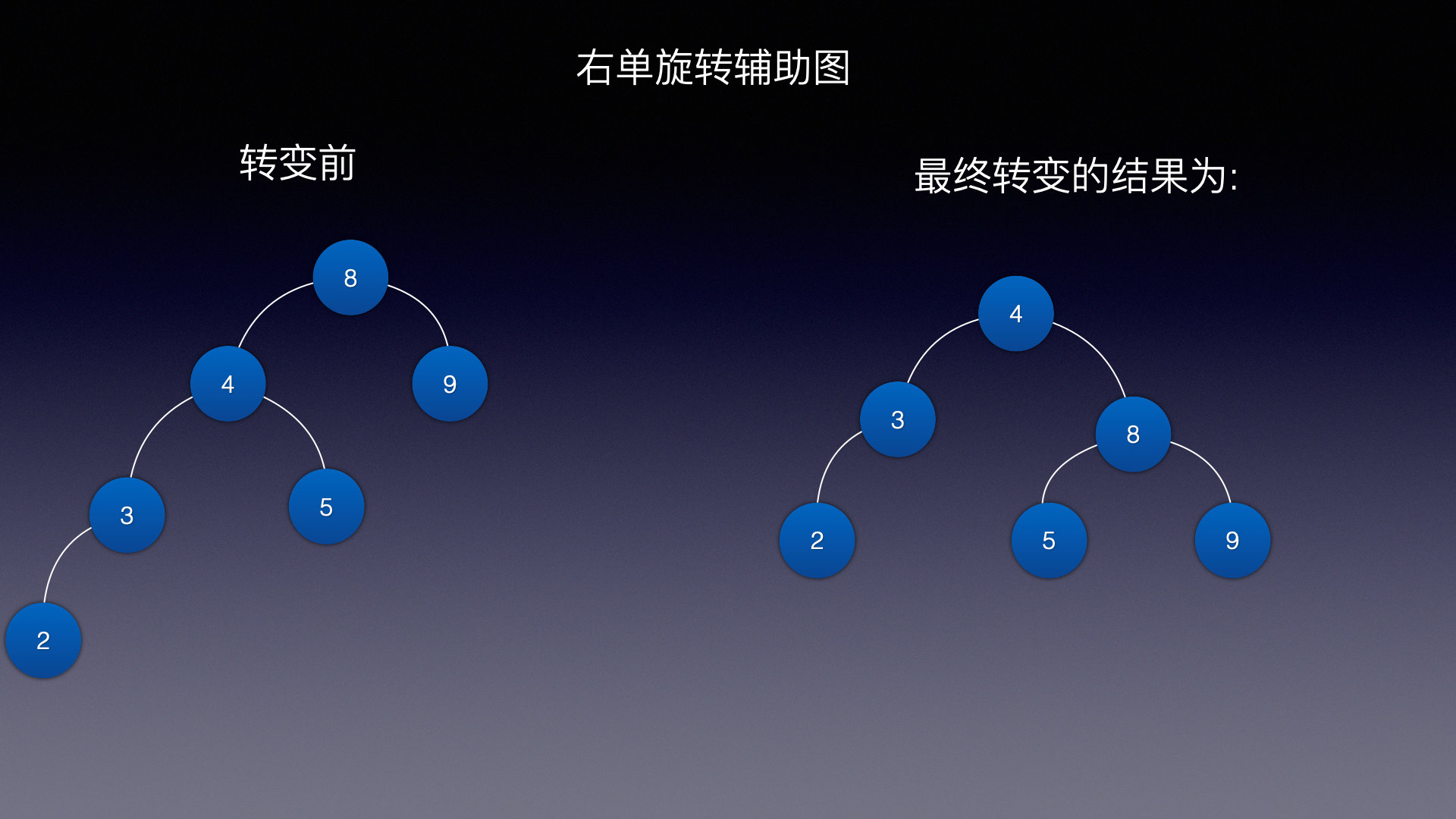
如果左子树高度 - 右子树高度 >= 2 说明这棵树已经不平衡了,需要右旋
来看看右旋代码
# AVLNode.java
// 右旋
public void rightRotate()
// 1. 创建一个新结点 和 root结点相同
AVLNode newNode = new AVLNode(value);
// 2. 将原本left结点赋值到新结点上
newNode.rightNode = rightNode;
// 3. 将原本左结点的右结点 赋值到新结点的左结点上
newNode.leftNode = leftNode.rightNode;
// 4. 将根节点转变为左结点
value = leftNode.value;
// 5. 将根节点左结点赋值为左结点的左结点
leftNode = leftNode.leftNode;
// 6. 将新结点复制到左结点上
rightNode = newNode;
右旋和左旋步骤一样,都是分了6步! 只不过是相反的方向罢了
那么代码也很好写了
public void add(AVLNode node)
if (node == null)
return;
....
// 添加结点
// 右子树高度 - 左子树高度 >= 2 说明需要 '左旋转'
if ( rightHeight() - leftHeight() >= 2)
leftRotate();
// 左子树高度 - 右子树高度 >= 2 说明需要 '右旋转'
if (leftHeight() - rightHeight() >= 2)
rightRotate();
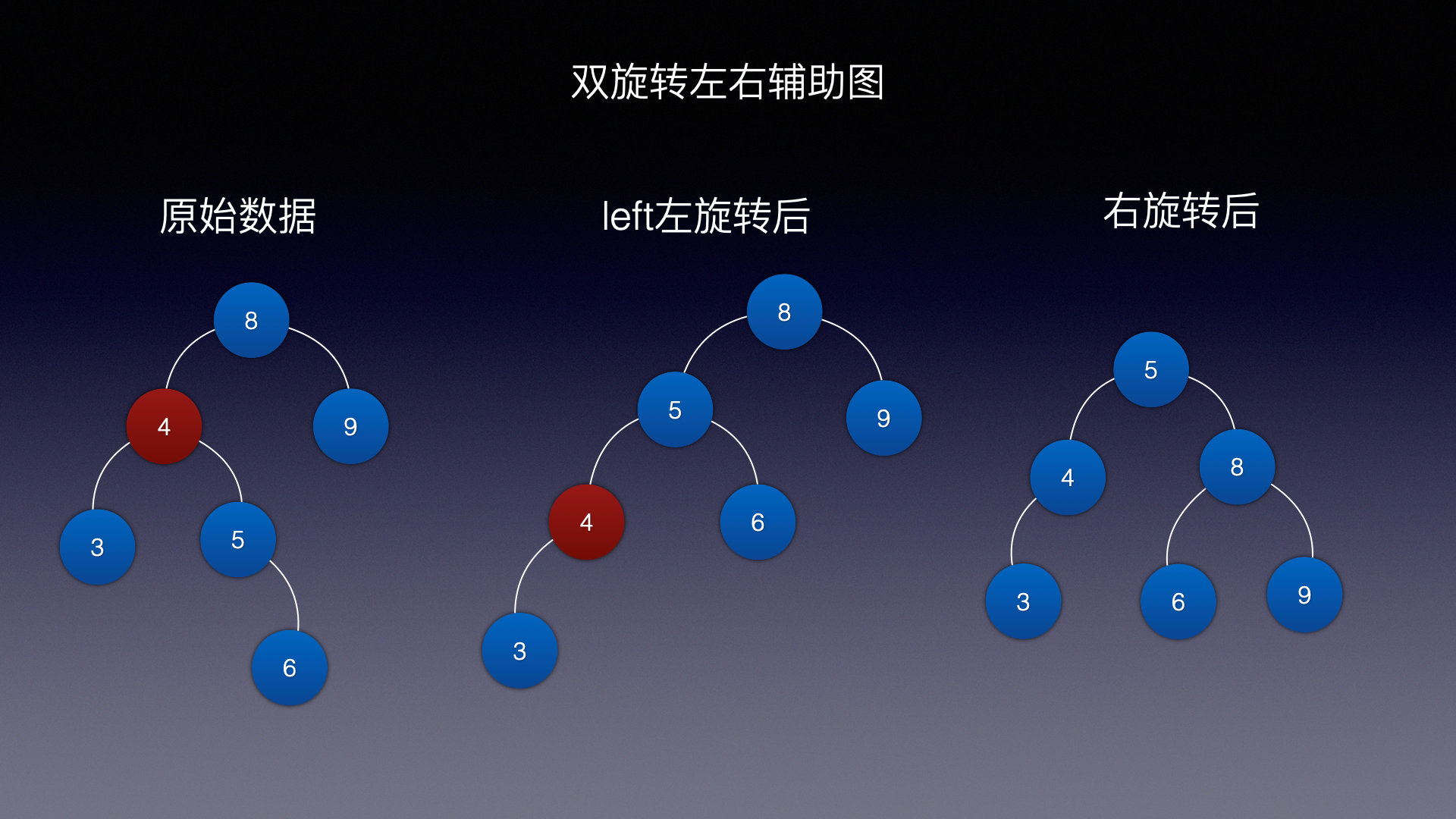
情况三 (左旋 右旋)
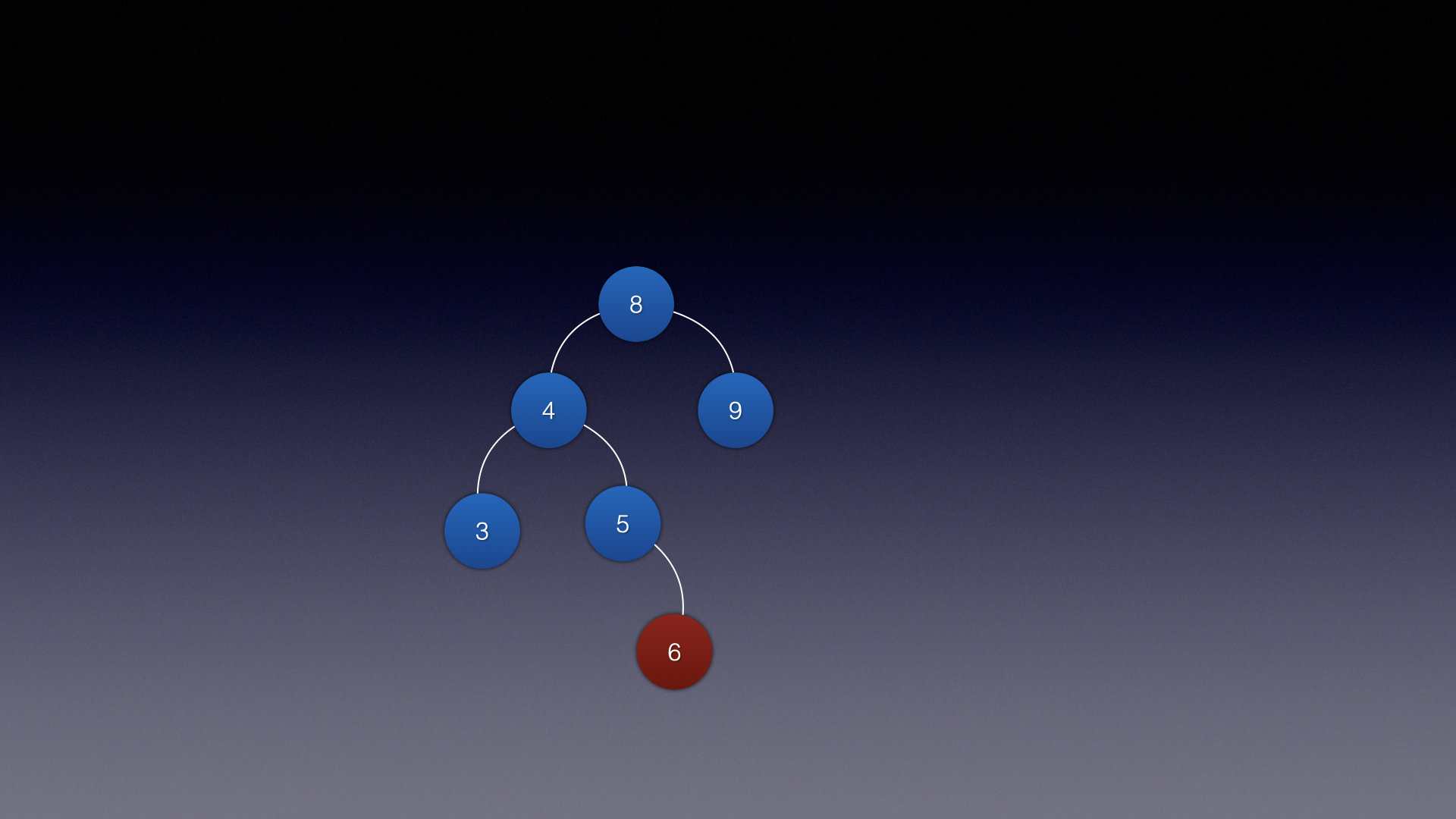
假设遇到这种情况,当前插入的结点是6,很显然破坏了AVL的平衡性
如果按照之前的情况旋转 左子树 比 右子树高 那么就进行右旋转
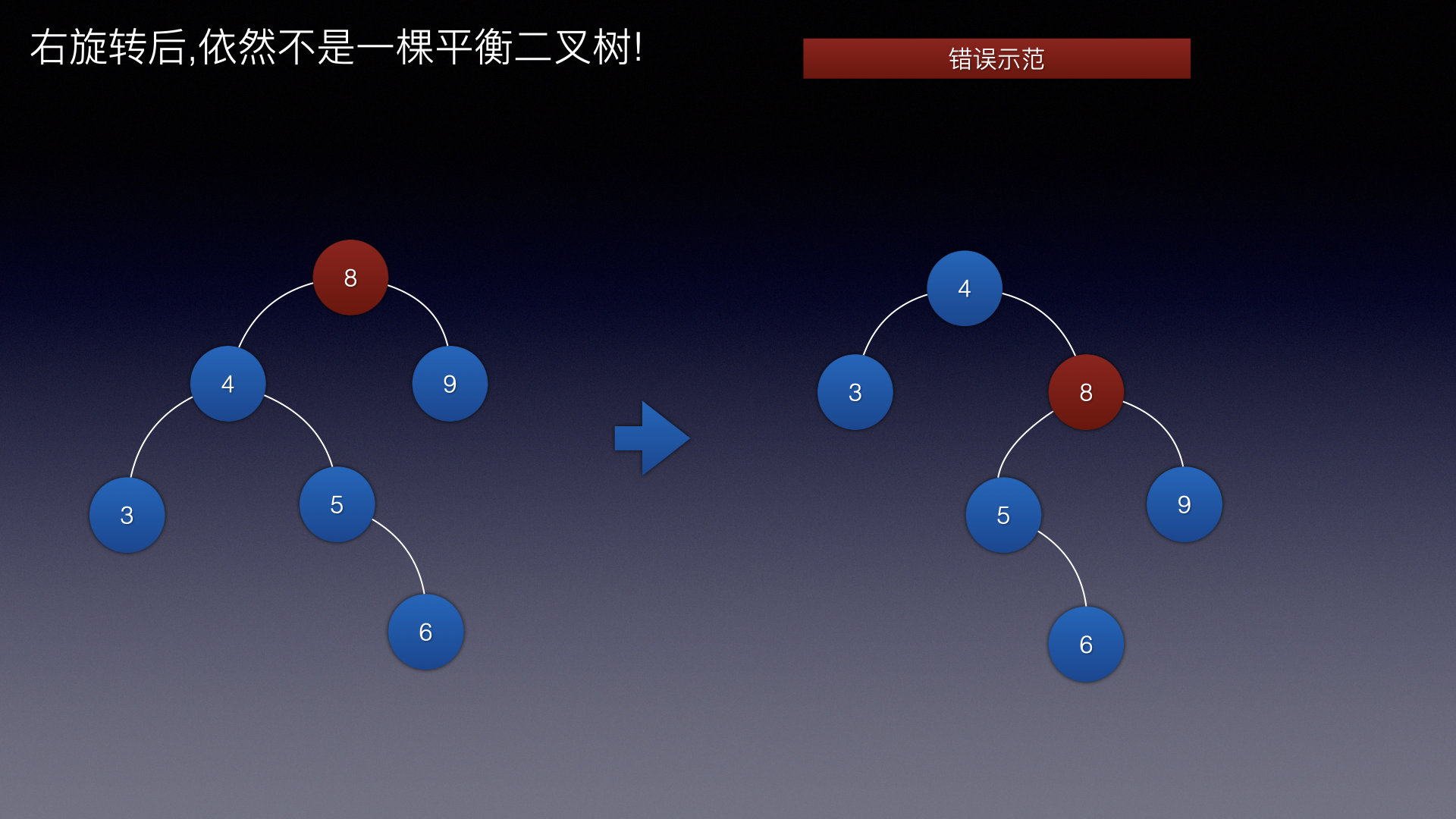
旋转过后还不是一个合格的AVL树!
现在出现的问题是:
根结点的左子结点的左子树 < 根结点左子结点的右子树
如果出现这种情况,想要平衡的话,又分为2步骤
- 根节点的左子结点 先向左旋转
- 然后以根节点为支点向右旋转
根节点的左子结点 先向左旋转:
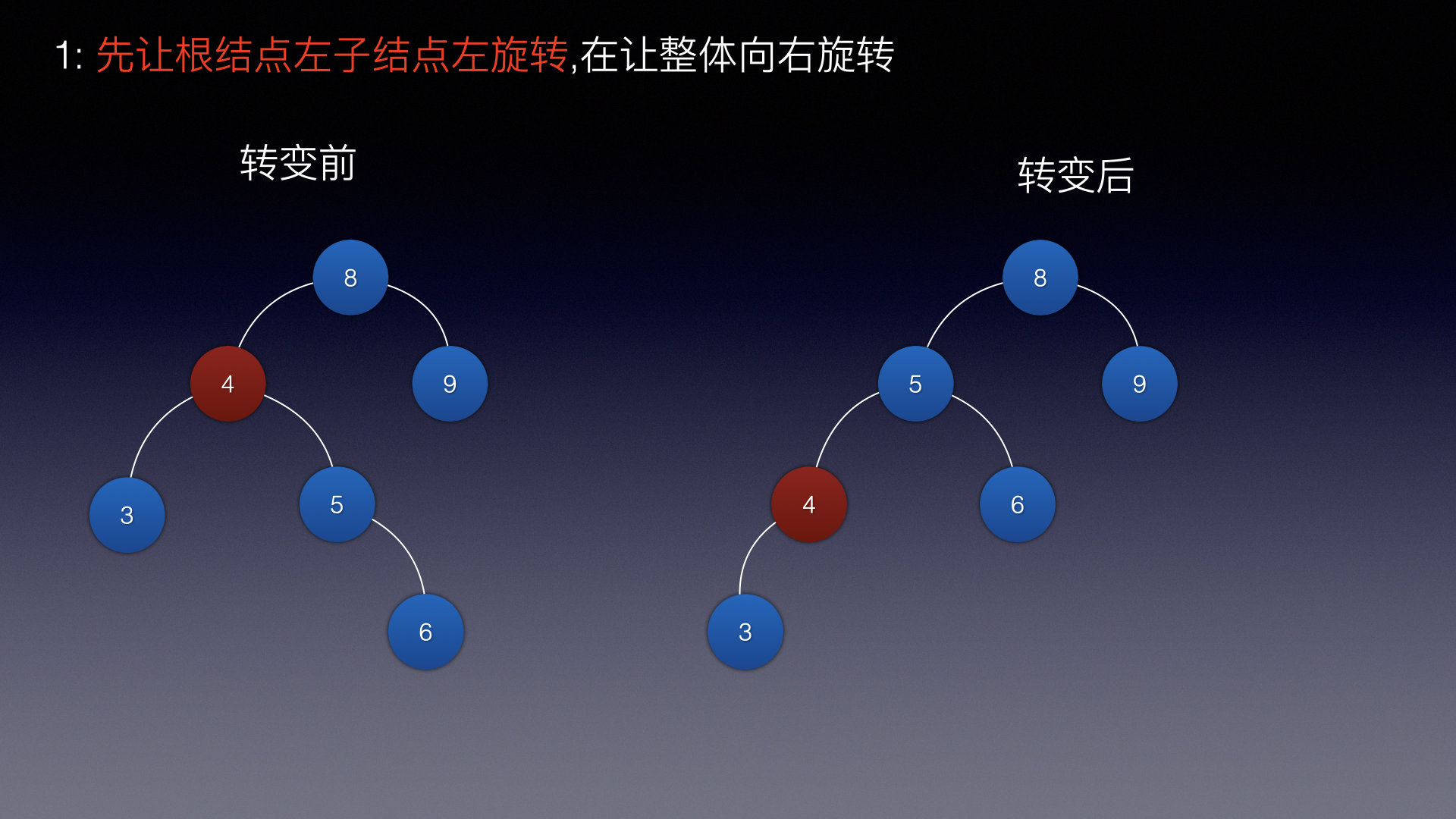
然后以根节点为支点向右旋转:
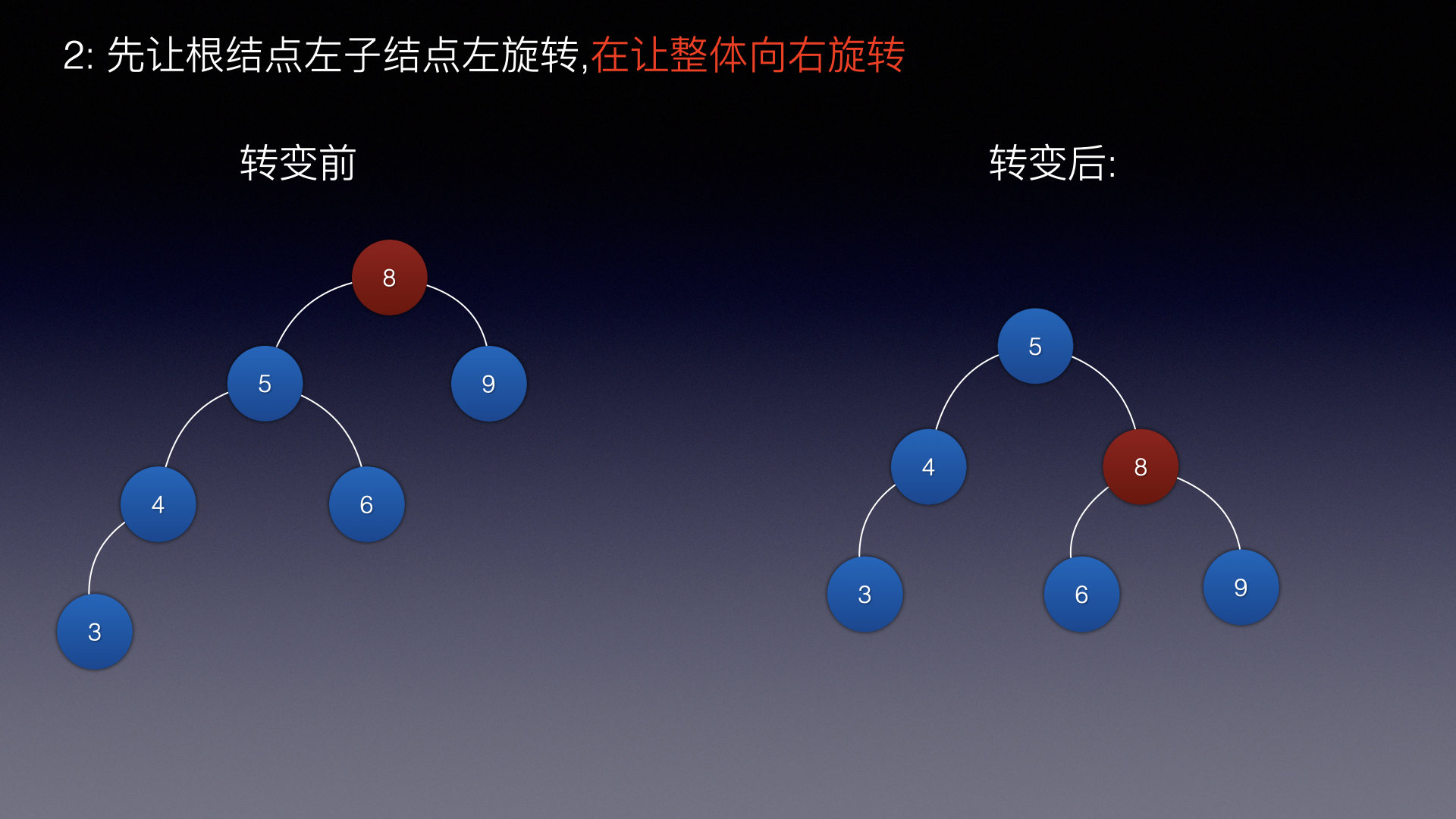
来看看代码怎么写:
# AVLNode.java
public void add(AVLNode node)
if (node == null)
return;
....
// 添加结点
// 右子树高度 - 左子树高度 >= 2 说明需要 '左旋转'
if ( rightHeight() - leftHeight() >= 2)
leftRotate();
// 左子树高度 - 右子树高度 >= 2 说明需要 '右旋转'
if (leftHeight() - rightHeight() >= 2)
// 如果左子结点高度 < 右子结点高度
if (leftNode != null && leftNode.leftHeight() < leftNode.rightHeight())
// 先让left结点 左旋转
leftNode.leftRotate();
rightRotate();
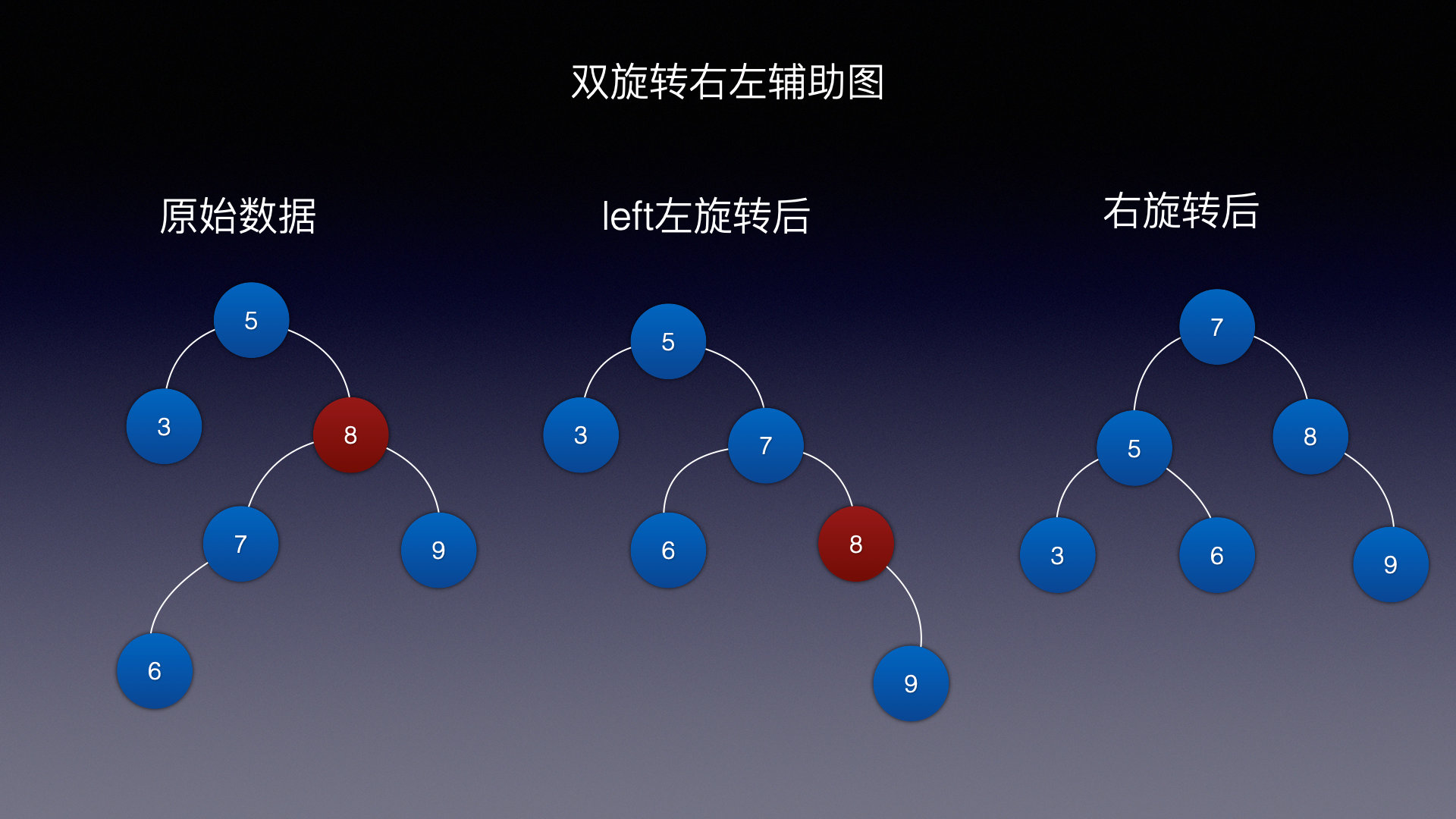
情况四 (右旋 左旋)
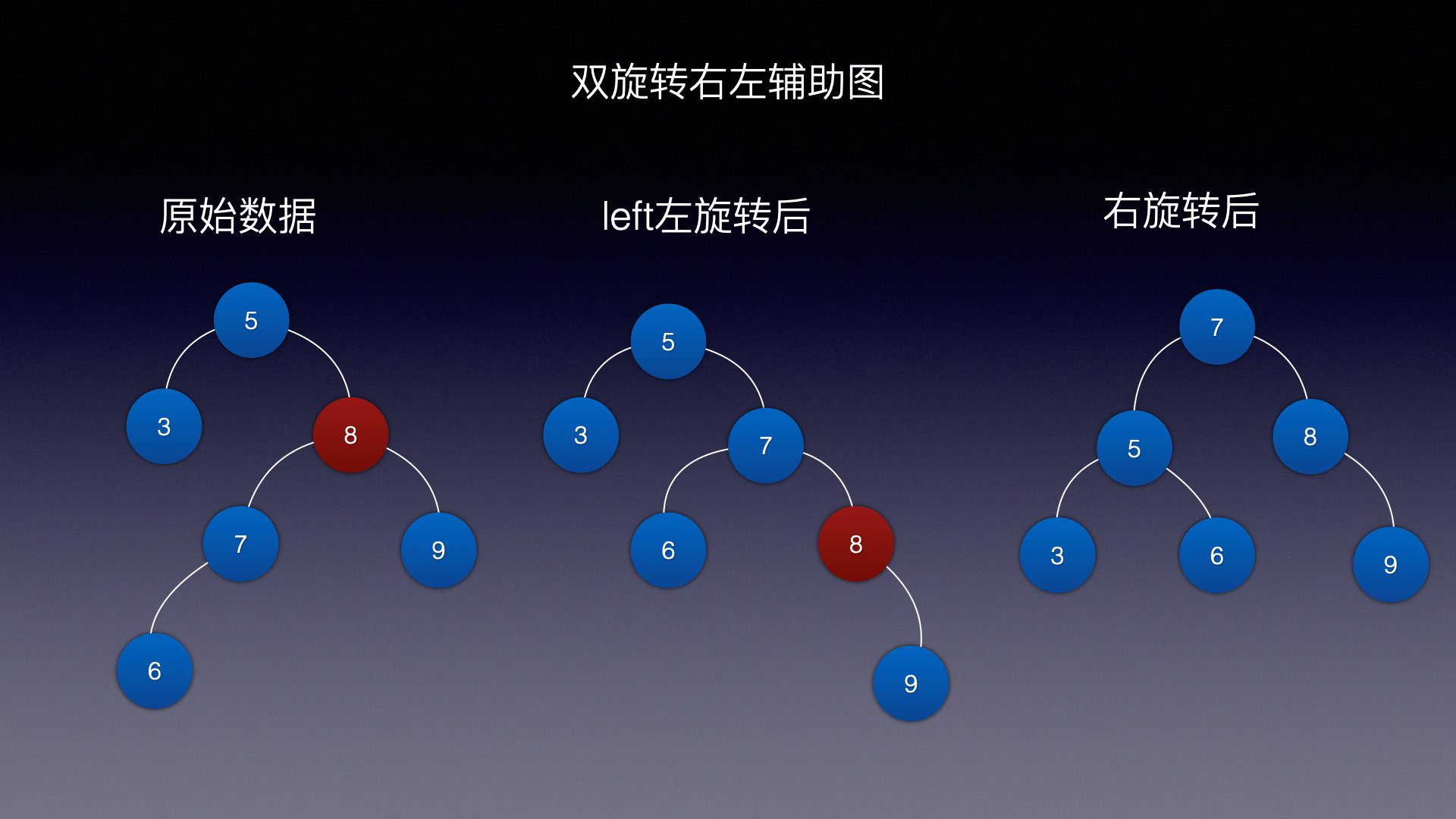
道理一样,直接看看添加的完整代码吧~
public void add(AVLNode node)
if (node == null)
return;
// 如果传入的结点 <= 当前结点
// 说明当前结点应该存放在左子结点上
if (node.value <= value)
// 如果左子结点为null 说明是叶子结点 直接存放即可
if (leftNode == null)
leftNode = node;
else
leftNode.add(node);
// 如果传入的结点 >= 当前结点
// 说明当前结点应该存放在右子结点上
if (node.value >= value)
// 如果左子结点为null 说明是叶子结点 直接存放即可
if (rightNode == null)
rightNode = node;
else
rightNode.add(node);
// 右子树高度 - 左子树高度 - >= 2 说明需要 '左旋转'
if (rightHeight() - leftHeight() >= 2)
if (rightNode != null && rightNode.leftHeight() > rightNode.leftHeight())
// 右旋转
rightNode.rightRotate();
leftRotate();
// 左子树高度 - 右子树高度 >= 2 说明需要 '右旋转'
if (leftHeight() - rightHeight() >= 2)
// 如果左子结点不为null 并且 左子结点高度 < 右子结点高度
// 说明需要先让left左旋转 在整体右旋转
if (leftNode != null && leftNode.leftHeight() < leftNode.rightHeight())
// 先让left结点 左旋转
leftNode.leftRotate();
// 在整体右旋转
rightRotate();
如果细细品味这4种情况,这还是很简单的!
删除结点
Tips: 删除结点也是根据上一篇:二叉排序树(BST)来写的,能够复用的代码全都复用了,只考虑不满足情况下如何处理即可!
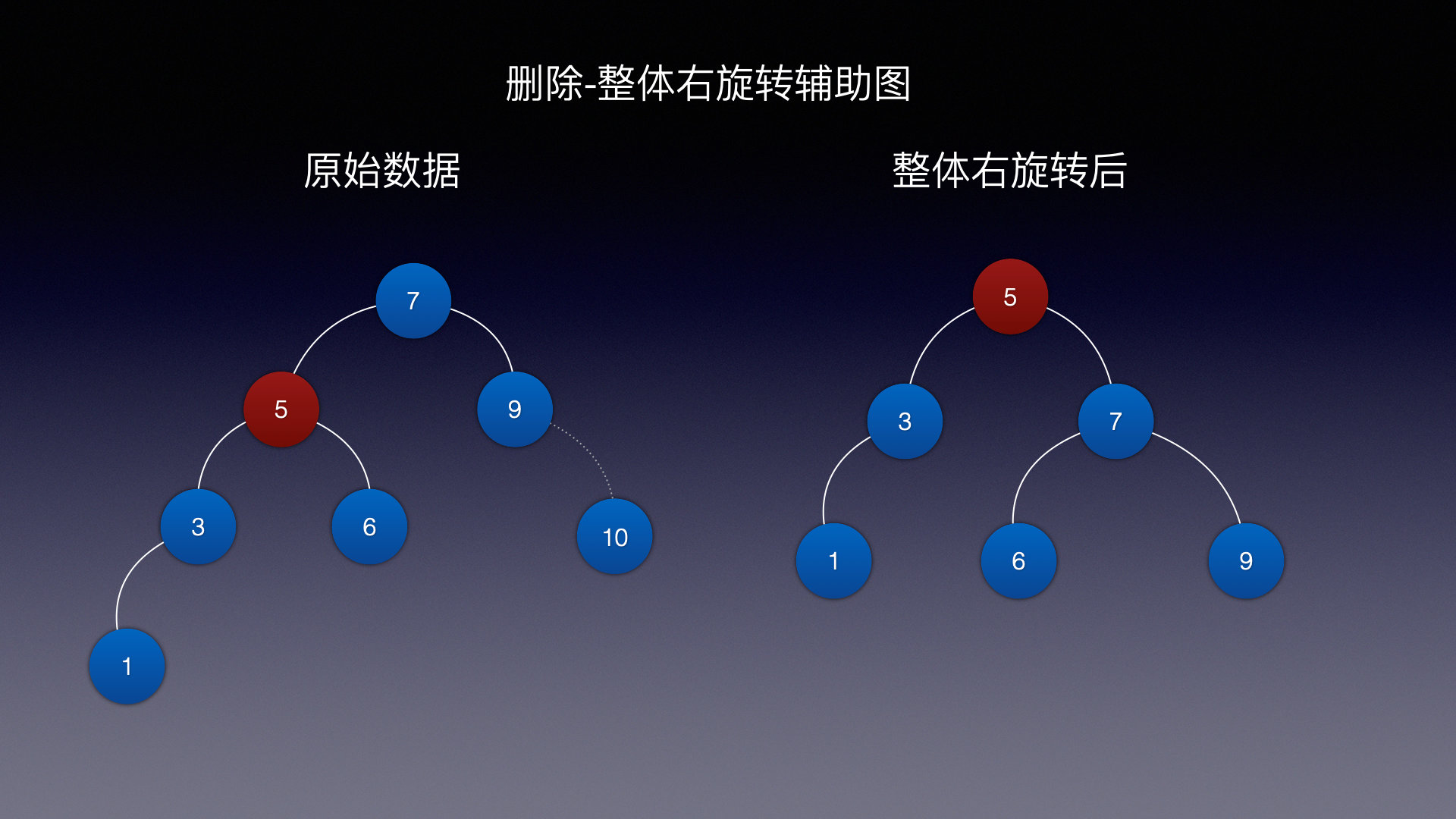
情况一 (右旋)

删除结点为10
- 判断 根结点左子树高度 和 根结点右子树高度
- 根结点左子树高度 > 根结点右子树高度 根结点右旋
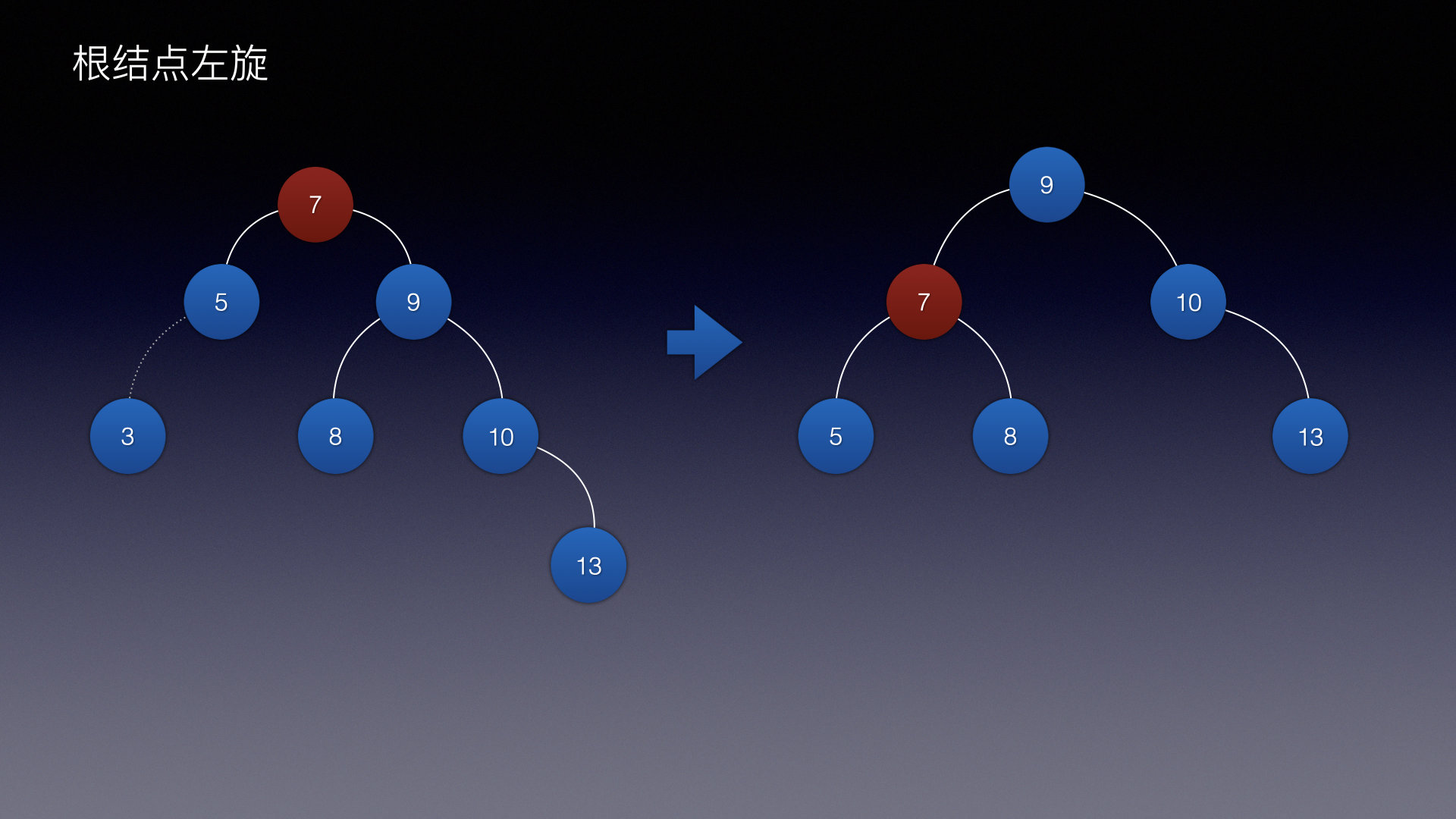
情况二(左旋)

删除结点为3
- 判断根结点左子树高度 和 根结点右子树高度
- 如果根结点右子树高度 > 根结点左子树高度
- 根结点左旋
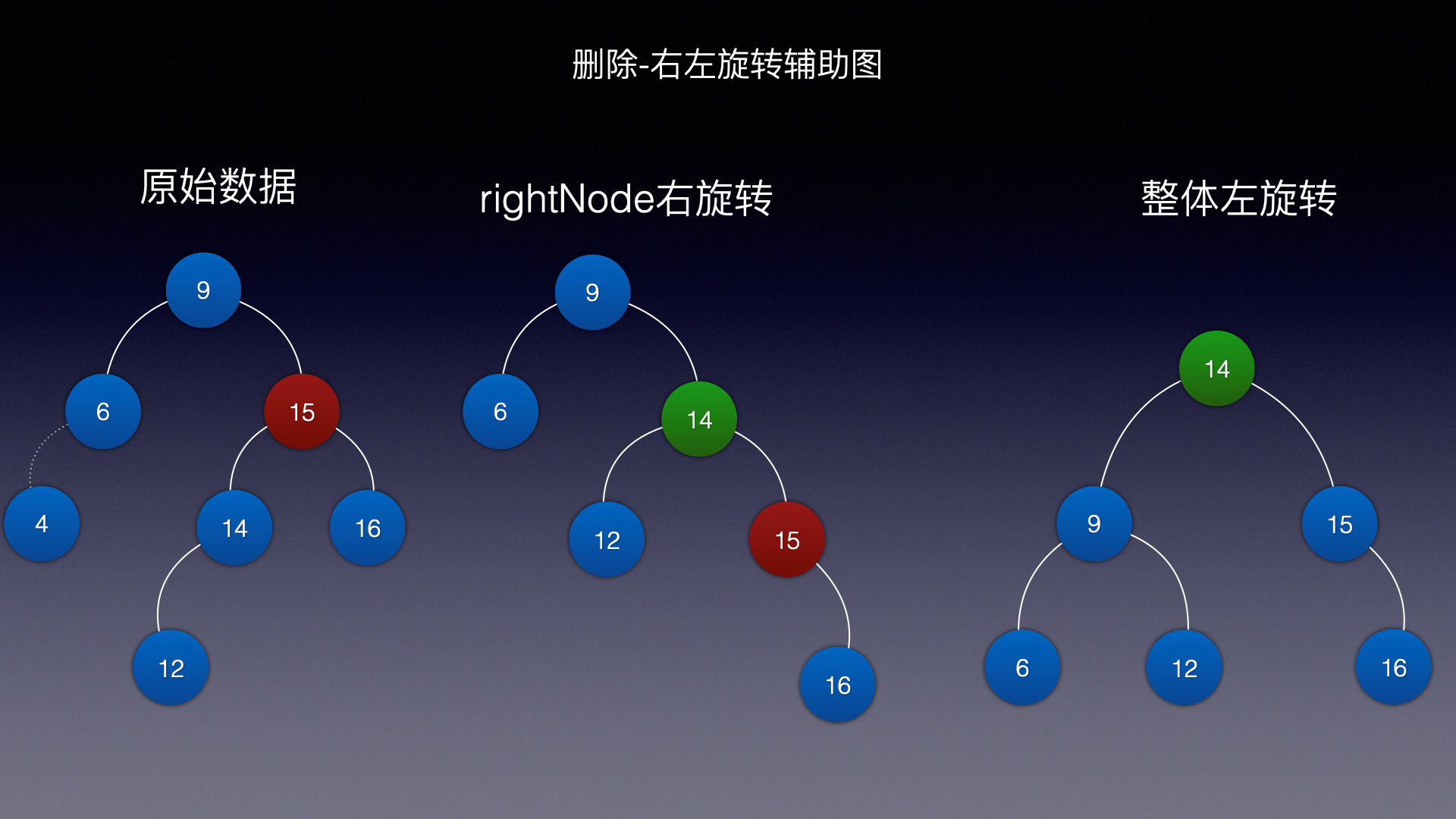
情况三 (右旋 左旋)

当前删除的结点是4
分为3步:
- 判断根结点
右子结点左子树高度和 根结点右子结点右子树高度 右子结点左子树高度>右子树右子结点高度,先让根结点右子结点右旋- 然后再让根结点左旋
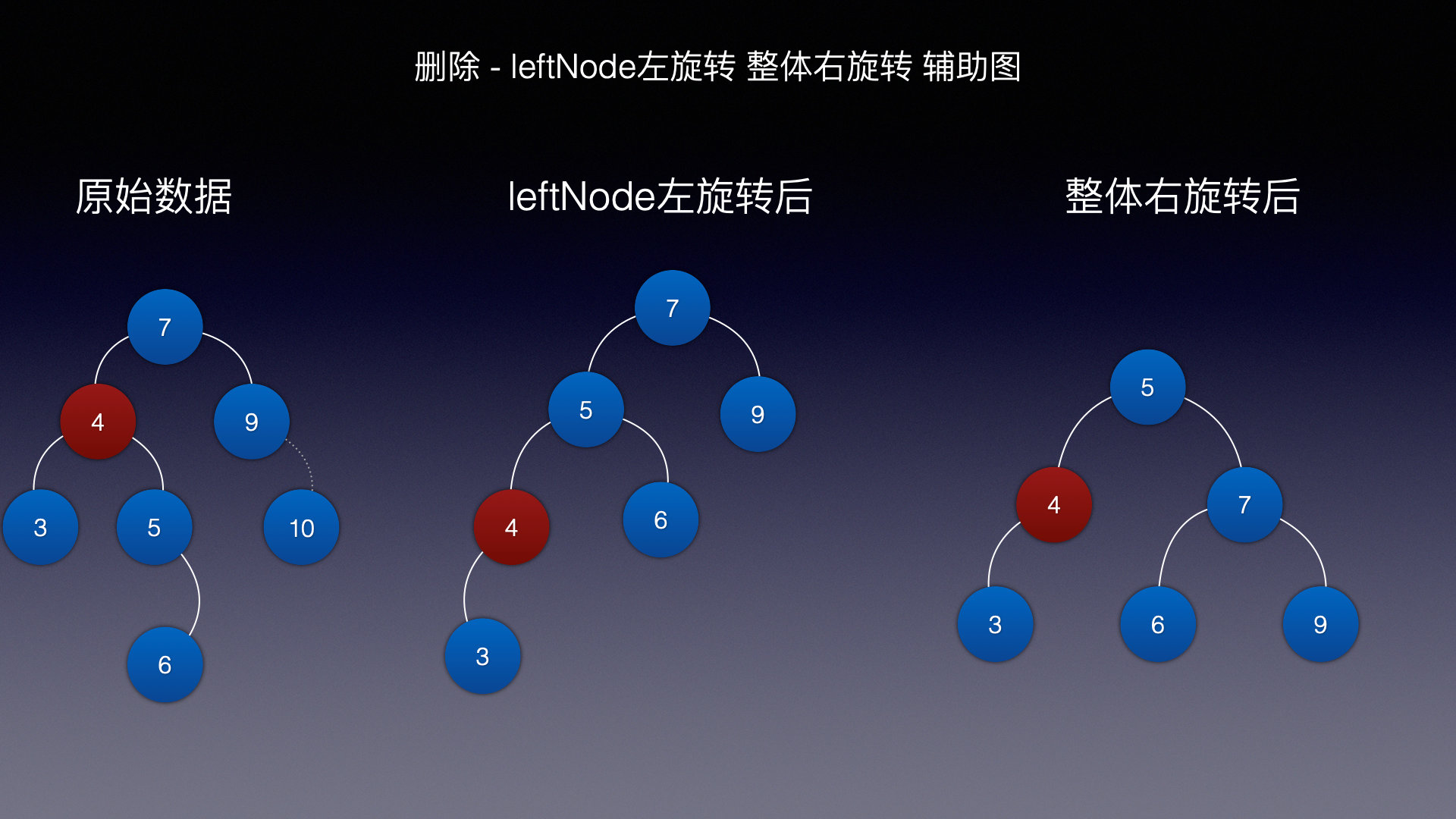
情况四 (左旋 右旋)

删除的节点是10
分为3步:
- 判断根结点左子结点左子树高度 和 跟结点左子树右子树高度
- 根结点左子结点右子树高度 > 根结点左子结点左子树高度,根结点左子结点左旋
- 然后根结点右旋
来看看删除完整代码:
# AVLNode.java
public void del(int value)
// 判断当前结点是左子结点还是 右子结点
// TODO 当前结点
AVLNode searchNode = search(value);
if (searchNode == null)
System.out.println("没有找到结点");
return;
// TODO 当前结点的父结点
AVLNode searchParentNode = searchParent(value);
// 左子结点和右子结点为null 说明是叶子结点
// TODO 删除叶子结点
if (searchNode.leftNode == null && searchNode.rightNode == null)
// 如果左子结点和当前结点相同 那么就删除左子结点
....
else if (searchNode.leftNode == null)
// TODO 删除只有一个叶子结点
....
else if (searchNode.rightNode == null)
// TODO 删除只有一个叶子结点
....
else
// TODO 左子结点和右子结点都有值!
....
// 如果当前左侧高度 - 右侧高度 <= -2 说明需要旋转
if (leftHeight() - rightHeight() <= -2)
// 如果右结点 的左子结点高度 > 右子结点高度 说明需要先让右子结点右旋转 再让整体左旋转
if (rightNode != null && rightNode.leftHeight() > rightNode.rightHeight())
// 右结点 右旋转
rightNode.rightRotate();
// 整体左旋转
leftRotate();
// 如果当前左侧高度 - 右侧高度 >= 2 说明需要旋转
if (leftHeight() - rightHeight() >= 2)
if (leftNode != null && leftNode.leftHeight() < leftNode.rightHeight())
// 左结点 左旋转
leftNode.leftRotate();
// 整体右旋转
rightRotate();
原创不易,您的点赞就是对我最大的支持!
其他树结构文章:
- 二叉树入门
- 顺序二叉树
- 线索化二叉树
- 堆排序
- 赫夫曼树(一)
- 赫夫曼树(二)
- 赫夫曼树(三)
- 二叉排序树(BST)
- 平衡二叉排序树AVL本篇
- 2-3树,2-3-4树,B树 B+树 B*树 了解
- 数据结构与算法:树 红黑树 (十一)
以上是关于数据结构与算法:树 AVL平衡二叉排序树的主要内容,如果未能解决你的问题,请参考以下文章