平衡二叉搜索树（最小高度树）

Posted 2020-11-29 blairgrowing

　　

 

 

 

 

 

　　首先复习下二叉搜索树的定义：

　　在二叉搜索树中：

　　1.若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。

　　2. 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。

　　3.任意结点的左、右子树也分别为二叉搜索树

　　总结一下就是，树的中序遍历可以得到一个升序序列。

 

　　　　　　　　　　

 

 

 

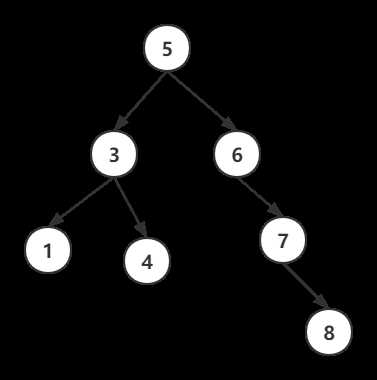
　　那如何保证高度最小呢？当树中的任意结点的左右子树高度差都不超过 1 时，整棵树的深度最小。

下面是一种构造最小高度树的思路：

　　（1）如果序列长度为 0，那么是一棵空树。
　　（2）如果序列长度为 1，那么只有一个根节点。
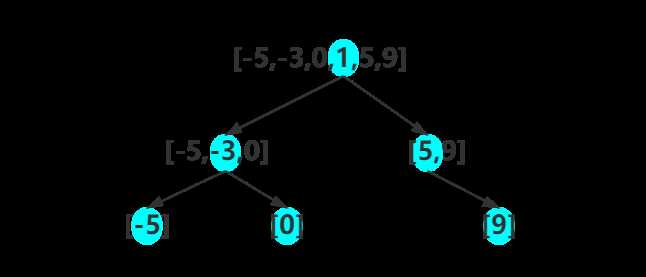
　　（3）如果长度大于 1，那么选取中间位置的数赋给根节点，然后前一半递归构建左子树，后一半递归构建右子树。

　　以 [-5,-3,0,1,5,9] 为例，构造过程如下图所示：

　　

 

 

#include<iostream>
#include<vector>
using namespace std;
struct TreeNode{
    int val;
    TreeNode * left;
    TreeNode *right;
    TreeNode(int x):val(x),left(NULL),right(NULL){}
};
TreeNode * dfs(const vector<int> &nums ,int L,int R){
    if(L>R) return nullptr;
    int mid=(L+R)>>1;
    TreeNode ptr = new TreeNode(num[mid]);//填充根节点
    ptr->left=dfs(nums,L,mid-1);//构造左子树
    ptr->right=dfs(nums,mid+1,R);//构造右子树
    return ptr;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
        return dfs(nums, 0, nums.size()-1);
}