三角形不等式。这个怎么用？

Posted 2023-05-10

看了一道题，上面有一个步骤是根据三角形不等式，可是我忘记了这个了，有这个定理吗？

就是 两个相加后的绝对值 小于等于 这两个绝对值的和

参考技术A 三角不等式是解决绝对值不等式的常用方法。有些绝对值不等式表面上难解但是在绝对值符号里面通过添项减项构造出三角形不等式解决起来很轻松。a|-|b|≤|a±b|≤|a|+|b| 参考技术B 三角不等式是解决绝对值不等式的常用方法。有些绝对值不等式表面上难解但是在绝对值符号里面通过添项减项构造出三角形不等式解决起来很轻松。 参考技术C |a|-|b|≤|a±b|≤|a|+|b|本回答被提问者采纳 参考技术D 不知道你什么意思
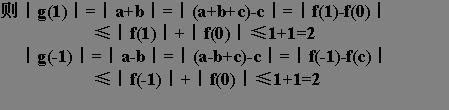
这个|a+b|≤|a|+|b|是有的啊

代数不等式与超越不等式

前言

超越不等式

如果不等式的两边至少有一个是超越函数，则称这个不等式为超越不等式。如\(2^x>x-1\)，包括指数不等式、对数不等式、三角不等式和反三角不等式等。

备注：代数函数¹；超越函数²；代数不等式³；

超越不等式求解思路

例1求解关于\(x\)的不等式\((2^x)-3\cdot 2^x+2<0\)；

分析：换元法，令\(2^x=t>0\)，则原超越不等式可以等价转化为代数不等式，不过是带有条件的，比如\(t>0\);

转化为\(t^2-3t+2<0(t>0)\)，用求解代数不等式的相应方法求解，

解得\(1<t<2\)，即\(1<2^x<2\)，解得\(0<x<1\)，

故所求的解集为\((0，1)\)。

例2求解关于\(x\)的不等式 \(2^x\geqslant 3-x\)

分析：不能使用代数不等式的求解方法，故想到数形结合的思路，

在同一个坐标系中做出两个函数\(y=2^x\)和\(y=3-x\)的图像，其交点往往比较特殊；

由图像可知，不等式的解集为\([1，+\infty)\)。

引申：上述例子中的图像交点往往比较特殊，如果变为一般的情形呢？

例3求解关于\(x\)的不等式\(2^x\geqslant 4-x\)

分析：绝大多数的题目的交点坐标往往比较特殊，我们都可以轻松解决；但不是所有题目都这样，比如本题目；

此时我们还是有办法的，就是用到零点存在性定理和二分法，

令函数\(f(x)=2^x+x-4\)，则\(f(1)=-1<0\)，\(f(2)=2>0\)，故函数的零点\(x_0\)一定满足\(x_0\in (1，2)\)，能不能将有解区间再压缩呢？

用二分法，求解\(f(1.5)=2^1.5+1.5-4\approx 0.3>0\)，故有解区间压缩为\((1，1.5)\)之间，

如果还嫌不够，继续求解\(f(1.25)=2^1.25+1.25-4\approx 0.1\)，\(2^1=2^\frac44<2^1.25=2^\frac54<2^\frac64=2\sqrt2\)；

---

1. 代数函数
   变量之间的关系是用有限次加、减、乘、除、乘方、开方运算表示的函数。如\(y=x^3+2x^2\)\(-x+1\)，\(y=\sqrtx-3\)等；?

2. 超越函数
   是指变量之间的关系不能用有限次加、减、乘、除、乘方、开方运算表示的函数。如对数函数\(y=log_2^x\)，反三角函数如\(y=arcsinx\)，指数函数如\(y=2^x\)，三角函数如\(y=sinx\)等就属于超越函数，它们属于初等函数中的初等超越函数。对数和指数函数即为超越函数的例子。?

3. 代数不等式
   不等式两边的函数，如果都是代数函数，则称这个不等式为代数不等式，如\(\cfrac2x-1>2x+1\)；可以划分为有理不等式(整式不等式和分式不等式)和无理不等式；?