矩阵权（Matrix weighted）Bezier三角（曲面）片

Posted 2022-06-23 拉风小宇

参考文献仍然是杨老师的这篇

Matrix weighted rational curves and surfaces

文章，结合上篇博文中的算法，再次将其引申到三角面片上

算法描述

假设$P_i,j,k,0\\leq i,j,k\\leq n,i+j+k=n$是给定的控制点，并且$M_ijk$是对应的加权矩阵。矩阵权有理三角面片由下式定义

$$Q_3(u,v,w)=[\\sum_i+j+k=nM_ijkB^n_i,j,k(u,v,w)]^-1\\sum_i+j+k=nM_ijkP_i,j,kB^n_i,j,k(u,v,w)，\\\\ (u,v)\\in[u_k_1-1,u_m+1]\\times[v_k_2-1,v_n+1]$$
其中 $B^n_i,j,k(u,v,w)=\\fracn!i!j!k!$是定义在三角域上的Berstein基函数。

代码实现

用matlab编写的如下程序为实现函数wm_tri.m

function trepBer = wm_tri( controls,num,M,N )
%WM_TRI Summary of this function goes here
%   Detailed explanation goes here
points=cell(num,num);
for i=1:num
    for j=1:i
        pointsi,j=[(j-1)*(1/(num-1)),1-(i-1)*(1/(num-1)),(i-j)*(1/(num-1))];
    end
end

n=size(controls,1);



Bpoints=cell(num,num);
for i=1:num
    for j=1:i
        Bpointsi,j=[0;0;0];
        tempM=zeros(3);
        for u=1:n
            for v=1:u
                %i=v-1;j=n-u;k=u-v
                tempM=tempM+Mu+v-1*factorial(n-1)/(factorial(v-1)*factorial(n-u)*factorial(u-v))*(pointsi,j(1)^(v-1)*pointsi,j(2)^(n-u)*pointsi,j(3)^(u-v));
                Bpointsi,j=Bpointsi,j+Mu+v-1*controlsu,v'*factorial(n-1)/(factorial(v-1)*factorial(n-u)*factorial(u-v))*(pointsi,j(1)^(v-1)*pointsi,j(2)^(n-u)*pointsi,j(3)^(u-v));
            end
        end
        Bpointsi,j=(tempM\\Bpointsi,j)';
    end
end


triConPoi=zeros(n*(n+1)/2,3);
temp=1;
for i=1:n
    for j=1:i
       triConPoi(temp,:)=controlsi,j;
       temp=temp+1;
    end
end

triConSur=zeros((n-1)^2,3);
temp=1;
for i=2:n%the first in the i-th line is n(n-1)/2
    for j=1:i-1
        %Counter clockwise order,up triangle
        triConSur(temp,:)=[i*(i-1)/2+j,i*(i-1)/2+j+1,i*(i-1)/2+j+1-i];
        temp=temp+1;
    end
end
for i=2:n-1%the first in the i-th line is n(n-1)/2
    for j=1:i-1
        %Counter clockwise order,down triangle
        triConSur(temp,:)=[i*(i-1)/2+j+1,i*(i-1)/2+j,i*(i-1)/2+j+1+i];
        temp=temp+1;
    end
end
trepCon=triangulation(triConSur,triConPoi); 


triBezPoi=zeros(n*(n+1)/2,3);
temp=1;
for i=1:num
    for j=1:i
       triBezPoi(temp,:)=Bpointsi,j;
       temp=temp+1;
    end
end
triBerSur=zeros((num-1)^2,3);
temp=1;
for i=2:num%the first in the i-th line is n(n-1)/2
    for j=1:i-1
        %Counter clockwise order,up triangle
        triBerSur(temp,:)=[i*(i-1)/2+j,i*(i-1)/2+j+1,i*(i-1)/2+j+1-i];
        temp=temp+1;
    end
end
for i=2:num-1%the first in the i-th line is n(n-1)/2
    for j=1:i-1
        %Counter clockwise order,down triangle
        triBerSur(temp,:)=[i*(i-1)/2+j+1,i*(i-1)/2+j,i*(i-1)/2+j+1+i];
        temp=temp+1;
    end
end
trepBer=triangulation(triBerSur,triBezPoi); 

trisurf(trepCon,'edgecolor','k','FaceColor', 'interp');alpha(.2);axis equal;hold on;
trisurf(trepBer,'edgecolor','none','FaceColor', 'interp');alpha(.9);hold on;
for i=1:3
quiver3(triConPoi(i,1),triConPoi(i,2),triConPoi(i,3),N(i,1),N(i,2),N(i,3),'r','filled','LineWidth',2);hold on;
end

end

示例

下面绘制一个瞅瞅哈

controls = cell(2,2);
controls1,1=[0,0,0];
controls2,1=[0.5,1,-0.2];controls2,2=[-0.4,0.9,0.1];

N=[0.1,-0.3,0.6;0.4,0.3,0.6;-0.3,0.4,0.4];

omega=ones(3,1);
niu=ones(3,1);
M=cell(3,1);

for i=1:3
S=sqrt(N(i,1)^2+N(i,2)^2+N(i,3)^2);
N(i,1)=N(i,1)/S;
N(i,2)=N(i,2)/S;
N(i,3)=N(i,3)/S;
end

I=[1 0 0;0 1 0;0 0 1];
for i=1:3
Mi=omega(i)*(I+niu(i)*N(i,:)'*N(i,:));
end

trepBer = wm_tri( controls,30,M,N);

结果如下图

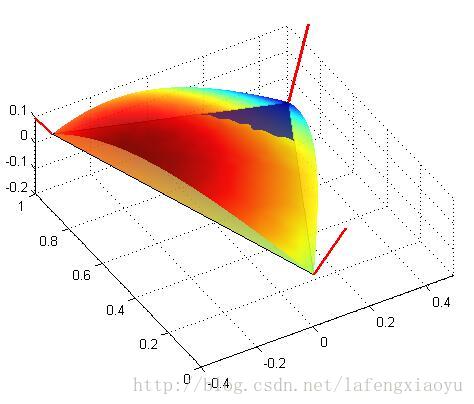
再来一个例子

来一整个模型瞅瞅，比如说人脸的例子

原本的网格	Bezier曲面片

老铁没毛病