权值衰减weight decay的理解

Posted 2023-03-30 @BangBang

1. 介绍

权值衰减weight decay即L2正则化，目的是通过在Loss函数后加一个正则化项，通过使权重减小的方式，一定减少模型过拟合的问题。

• L1正则化：即对权重矩阵的每个元素绝对值求和，$\lambda \ast ||W||$
• L2正则化：即对权重矩阵的每个元素求平方和（先平方，后求和）:
  $$1/2\ast \lambda \ast ||W|{|}^2$$

注意：正则化项不需要求平均数，因为权重矩阵和样本数量无关，只是为了限制权重规模。

L1损失函数：最小化绝对误差，因此L1损失对异常点有较好的适应更鲁棒，不可导，有多解，解的稳定性不好。关于L1损失函数的不连续的问题，可以通过平滑L1损失函数代替：

L2损失函数：最小化平方误差，因此L2损失对异常点敏感，L2损失函数会赋予异常点更大的损失值和梯度，调整网络参数向减小异常点误差的方向更新，因此容易造成训练的不稳定和发散。仅有一解，解的稳定更好

2. weight decay的作用

从直观上讲，L2正则化(weight decay)使得训练的模型在兼顾最小化分类（或其他目标）的Loss的同时，使得权重w尽可能地小，从而将权重约束在一定范围内，减小了模型的复杂度；同时，如果将w约束在一定范围内，也能够有效防止梯度爆炸。

3. Pytorch中的L2正则项——weight decay

L2正则项本质上相当于是权值衰减，这是因为目标函数为:
$Obj=Cost+Regularization$, 在梯度下降公式中:

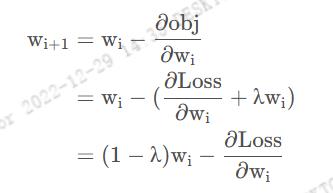
由于这里的正则化系数$\lambda$是一个介于0 到1之间数，因此可以看出，与不加正则项的梯度下降公式: $w_{i+1}=w_i-\frac{\partial Loss}{\partial w_i}$ 相比，相当于是做了一个权值的下降

Pytorch中的 weight decay 是在优化器中实现的，在优化器中加入参数weight_decay=即可，参数中的weight_decay等价于正则化系数$\lambda$。例如下面的两个随机梯度优化器，一个是没有加入正则项，一个加入了正则项，区别仅仅在于是否设置了参数weight_decay的值：

optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

4. weight decay效果示例

hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)

from tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter

set_seed(1)  # 设置随机种子
n_hidden = 200
max_iter = 2000
disp_interval = 200
lr_init = 0.01


# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):

   w = 1.5
   train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
   train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
   test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
   test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())

   return train_x, train_y, test_x, test_y


train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))


# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
   def __init__(self, neural_num):
       super(MLP, self).__init__()
       self.linears = nn.Sequential(
           nn.Linear(1, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, 1),
       )

   def forward(self, x):
       return self.linears(x)


net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)

# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()

# ============================ step 5/5 迭代训练 ============================

writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):

   # forward
   pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
   loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

   optim_normal.zero_grad()
   optim_wdecay.zero_grad()

   loss_normal.backward()
   loss_wdecay.backward()

   optim_normal.step()
   optim_wdecay.step()

   if (epoch+1) % disp_interval == 0:

       # 可视化
       for name, layer in net_normal.named_parameters():
           writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
           writer.add_histogram(name + '_data_normal', layer, epoch)

       for name, layer in net_weight_decay.named_parameters():
           writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)
           writer.add_histogram(name + '_data_weight_decay', layer, epoch)

       test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)

       # 绘图
       plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
       plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
       plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
       plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
       plt.text(-0.25, -1.5, 'no weight decay loss=:.6f'.format(loss_normal.item()), fontdict='size': 15, 'color': 'red')
       plt.text(-0.25, -2, 'weight decay loss=:.6f'.format(loss_wdecay.item()), fontdict='size': 15, 'color': 'red')

       plt.ylim((-2.5, 2.5))
       plt.legend(loc='upper left')
       plt.title("Epoch: ".format(epoch+1))
       plt.show()
       plt.close()

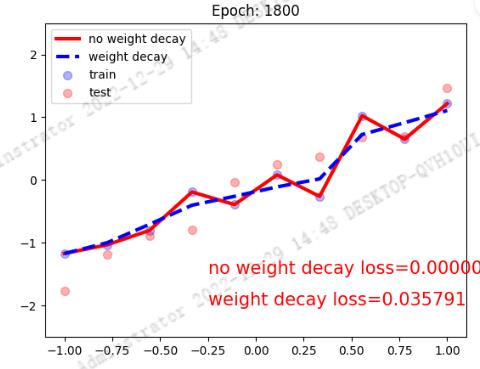
红色曲线为没有 weight decay 的结果，蓝色虚线为加入 weight decay 的训练结果，可以看到加入后能够非常有效的缓解过拟合现象。

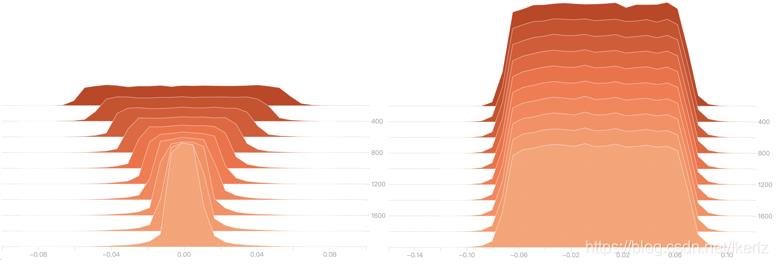
下图为第二层的权值柱状图，左边为加入正则项，右边为没有加正则项，可以看出，左边的权值确实有一个递减的趋势，而右边几乎是保持不变的状态。

参考：深度之眼Pytorch框架训练营第四期——正则化之weight decay

神经网络权重衰减（weight-decay）

权重衰减（weight-decay）

• 权重衰减
• • 方法
  • 高维线性回归实验
  • 从零开始实现
  • • 初始化模型参数
    • 定义$L_2$范数惩罚项
    • 定义训练和测试
    • 观察过拟合
    • 使用权重衰减
  • 简洁实现
  • 小结

权重衰减

上一节中我们观察了过拟合现象，即模型的训练误差远小于它在测试集上的误差。虽然增大训练数据集可能会减轻过拟合，但是获取额外的训练数据往往代价高昂。本节介绍应对过拟合问题的常用方法：权重衰减（weight decay）。

方法

权重衰减等价于 $L_2$ 范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。我们先描述$L_2$范数正则化，再解释它为何又称权重衰减。

$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项，从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以3.1节（线性回归）中的线性回归损失函数

$$\ell (w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right)}^2$$

为例，其中$w_1,w_2$是权重参数，$b$是偏差参数，样本$i$的输入为$x_1^{(i)},x_2^{(i)}$，标签为$y^{(i)}$，样本数为$n$。将权重参数用向量$\mathbf{w}=[w_1,w_2]$表示，带有$L_2$范数惩罚项的新损失函数为

$$\ell (w_1,w_2,b)+\frac{\lambda }{2n}\Vert \mathbf{w}{\Vert }^2,$$

其中超参数 $\lambda >0$。当权重参数均为0时，惩罚项最小。当$\lambda$较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时，惩罚项完全不起作用。

上式中$L_2$范数平方$\Vert \mathbf{w}{\Vert }^2$展开后得到$w_1^2+w_2^2$。有了$L_2$范数惩罚项后，在小批量随机梯度下降中，我们将线性回归一节中权重$w_1$和$w_2$的迭代方式更改为：

$$\begin{array}{rl}{w}_1& \leftarrow \left(1-\frac{\eta \lambda }{|\mathcal{B}|}\right)w_1-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{x}_1^{(i)}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right),\\ w_2& \leftarrow \left(1-\frac{\eta \lambda }{|\mathcal{B}|}\right)w_2-\frac{\eta }{|\mathcal{B}|}\end{array}$$

神经网络权重衰减（weight-decay）

weight decay

从keras中SGD源码理解基于时间的学习速率衰减decay策略

Tensorflow实现学习率衰减

TensorFlow深度学习实战---MNIST数字识别问题