Matrix 矩阵
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Matrix 矩阵相关的知识,希望对你有一定的参考价值。
CSS3中的矩阵指的是一个方法,书写为matrix()和matrix3d(),前者是元素2D平面的移动变换(transform),后者则是3D变换。2D变换矩阵为3*3, 如上面矩阵示意图;3D变换则是4*4的矩阵。
transform 里面的:斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)。本质上就是通过matrix实现的快捷方法(注意:
translate, rotate等方法都是需要单位的,而matrix方法e, f参数的单位可以省略。)transform-origin: 50px 70px; (向左移50,向上移70)代表的是transform的中心点(也就是下面的x, y)
开始:
transform: matrix(a,b,c,d,e,f);
(a表示缩放x轴,b和c影响拉伸,d表示缩放y轴,e水平偏移距离,f垂直偏移距离)
实际上,这6参数,对应的矩阵就是:


矩阵计算:
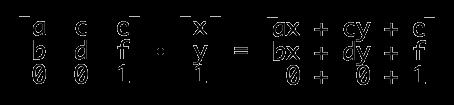
ax+cy+e,是由3*3矩阵每一行的第1个值与后面1*3的第1个值相乘,第2个值与第2个相乘,第3个与第3个,然后相加。ax+cy+e为变换后的水平坐标,bx+dy+f表示变换后的垂直位置。
举例:
transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */
假设元素中心点为: x = 0; y = 0;
变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30
也就是元素从(0, 0) 移动到右下方 (30, 30)(等同于transform: translate(30px, 30px);)
以上是关于Matrix 矩阵的主要内容,如果未能解决你的问题,请参考以下文章