第二节2:K-Means算法及其Python实现(算法实现结果展示)
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第二节2:K-Means算法及其Python实现(算法实现结果展示)相关的知识,希望对你有一定的参考价值。
文章目录
- 所用数据集及可视化代码均在本专栏文章中给出
四:Python实现
算法代码
cluster:该列表用于标识某个数据点属于哪一个簇;例如cluster[3] = 2,cluster[252] = 1,cluster[26] = 2标识3、252、26号数据点分别属于簇2、1、2,很显然3号和26号数据点属于同一个簇centroids:该列表用于记录质心,保存的是质心数据,便于在可视化时标记
import numpy as np
'''
1:随机初始化k个质心
2:计算每个样本点到这k个质心的距离,然后把它们分配到距其最近的质心所在的簇中
3:针对每个簇,计算属于该簇的所有样本的均值作为新的质心
4:重复步骤2和3,直到质心不再发生变化
'''
# 随机初始化质心
def centorids_init(data_set, k):
examples_nums = np.shape(data_set)[0] # 样本数量
random_ids = np.random.permutation(examples_nums) # 随机打乱序列
centorids = data_set[random_ids[:k], :] # 随机选取k质心
return centorids
# 计算距离实现划分
def compute_cluster(data_set, centorids):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids_nums = np.shape(centorids)[0] # 质心数量
cluster = np.zeros((examples_nums, 1)) # 返回结果
for examples_index in range(examples_nums):
distance = np.zeros(centorids_nums) # 保存examples_index这个样本点到各质心点的距离
for centorids_index in range(centorids_nums):
distance[centorids_index] = np.sqrt(np.sum(
np.power(data_set[examples_index, :]-centorids[centorids_index, :], 2)))
cluster[examples_index] = np.argmin(distance) # 最终在这些距离中选择出最小的一个
return cluster
# 用于更新质心
def renew_centoids(data_set, cluster, k):
features_num = data_set.shape[1] # 特征格式,即属性
centorids = np.zeros((k, features_num)) # k个簇每个都要计算,且每个簇的点都有features_num个属性,所以要对应计算
for centroid_id in range(k):
closest_ids = cluster == centroid_id # 不懂的话可以查阅 “Numpy布尔数组”相关内容
centorids[centroid_id] = np.mean(data_set[closest_ids.flatten(), :], axis=0)
return centorids
# 算法主体
def k_means(data_set, k, max_iterations):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids = centorids_init(data_set, k) # 随机选取k个质心
cluster = np.zeros(examples_nums) # 用于标识该样本点与那个质心最近,其本质就是划分的簇
for _ in range(max_iterations): # 不断迭代
# 计算距离且分配
cluster = compute_cluster(data_set, centorids)
# 更新质心
centorids = renew_centoids(data_set, cluster, k)
return centorids, cluster
五:效果展示
(1)Iris数据集(较好)
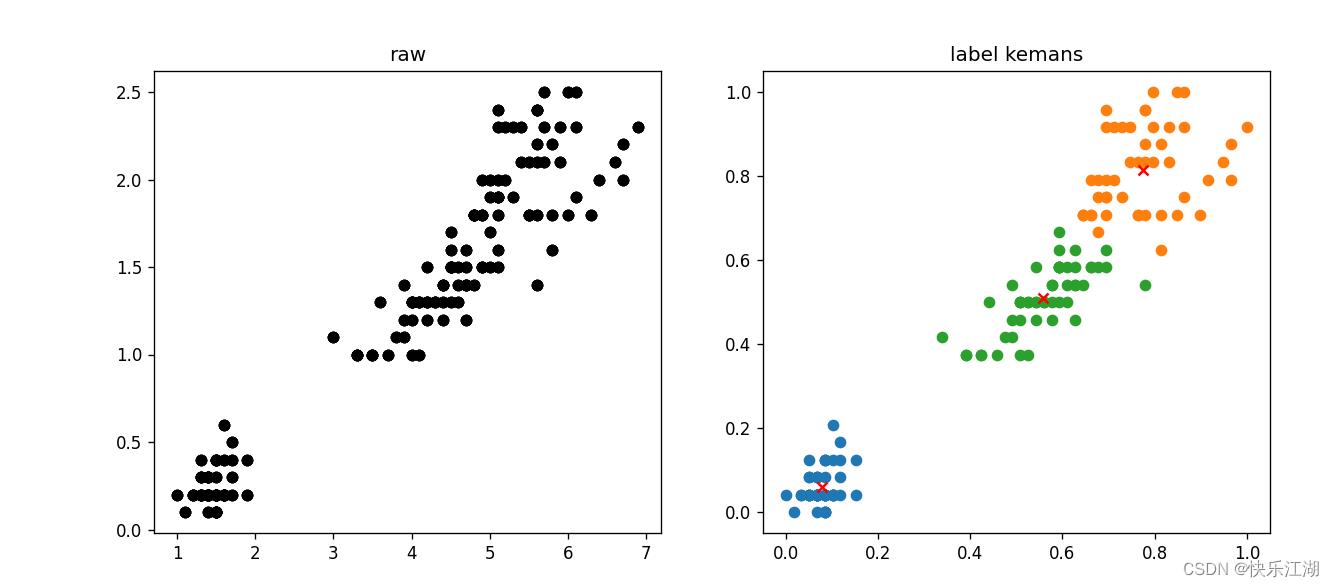
import pandas as pd
import matplotlib.pyplot as plt
import KMeans2
import numpy as np
Iris_types = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'] # 花类型
Iris_data = pd.read_csv('./Iris.csv')
x_axis = 'PetalLengthCm' # 花瓣长度
y_axis = 'PetalWidthCm' # 花瓣宽度
# x_axis = 'SepalLengthCm' # 花萼长度
# y_axis = 'SepalWidthCm' # 花萼宽度
examples_num = Iris_data.shape[0] # 样本数量
train_data = Iris_data[[x_axis, y_axis]].values.reshape(examples_num, 2) # 整理数据
# 归一化
min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))
# 训练参数
k = 3 # 簇数
max_iterations = 50 # 最大迭代次数
centroids, cluster = KMeans2.k_means(normal_data, k, max_iterations)
plt.figure(figsize=(12, 5), dpi=80)
# 第一幅图是已知标签或全部数据
plt.subplot(1, 2, 1)
for Iris_type in Iris_types:
plt.scatter(Iris_data[x_axis], Iris_data[y_axis], c='black')
plt.title('raw')
# 第二幅图是聚类结果
plt.subplot(1, 2, 2)
for centroid_id, centroid in enumerate(centroids): # 非聚类中心
current_examples_index = (cluster == centroid_id).flatten()
plt.scatter(normal_data[current_examples_index, 0], normal_data[current_examples_index, 1])
for centroid_id, centroid in enumerate(centroids): # 聚类中心
plt.scatter(centroid[0], centroid[1], c='red', marker='x')
plt.title('label kemans')
plt.show()
(2)人造数据集(好)
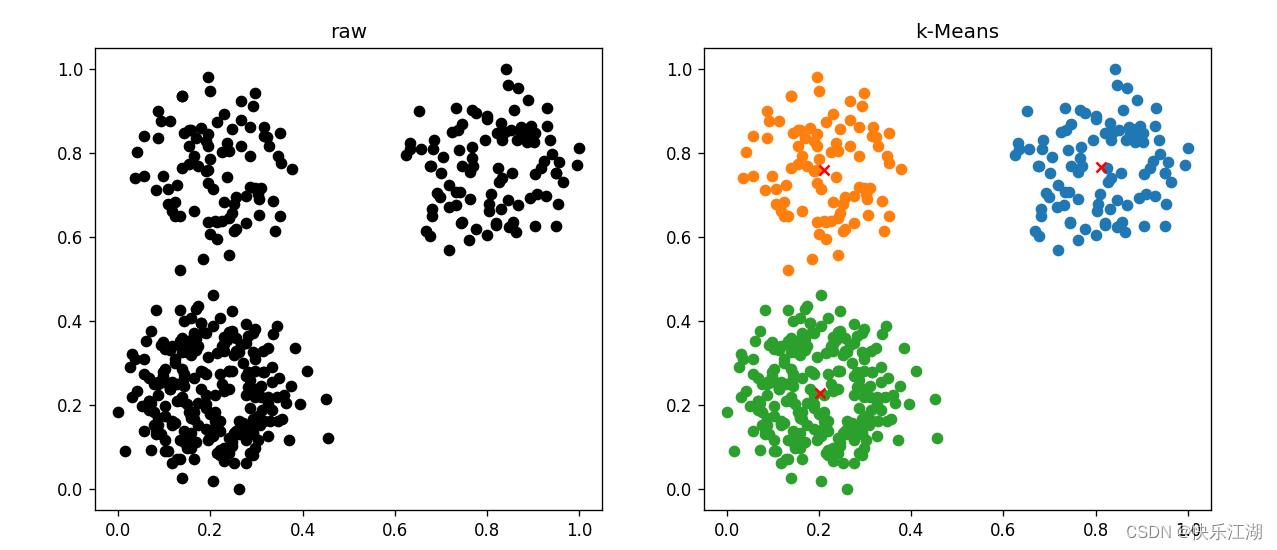
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import KMeans2
raw_data = pd.read_csv('./438-3.csv', header=None)
examples_num = raw_data.shape[0]
train_data = raw_data[[0, 1]].values.reshape(examples_num, 2)
# 归一化
min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))
print(normal_data)
# 训练参数
k = 3
max_iterations = 50
centroids, cluster = KMeans2.k_means(normal_data, k, max_iterations)
plt.figure(figsize=(12, 5), dpi=80)
# 第一幅图已知标签
plt.subplot(1, 2, 1)
plt.scatter(normal_data[:, 0], normal_data[:, 1], c='black')
plt.title('raw')
# 第二幅图聚类结果
plt.subplot(1, 2, 2)
for centroid_id, centroid in enumerate(centroids):
current_examples_index = (cluster == centroid_id).flatten()
plt.scatter(normal_data[current_examples_index, 0], normal_data[current_examples_index, 1])
for centroid_id, centroid in enumerate(centroids):
plt.scatter(centroid[0], centroid[1], c='red', marker='x')
plt.title('k-Means')
plt.show()
(3)Jain数据集(较差)
- 代码同(2)
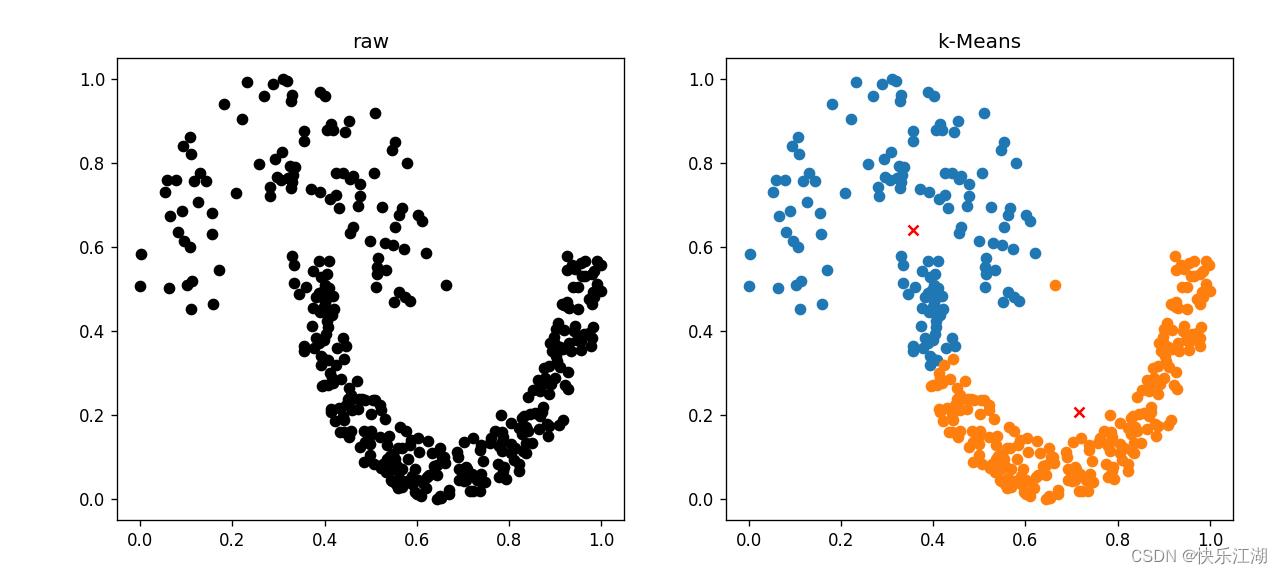
(4)melon数据集(好)
- 代码同(2)
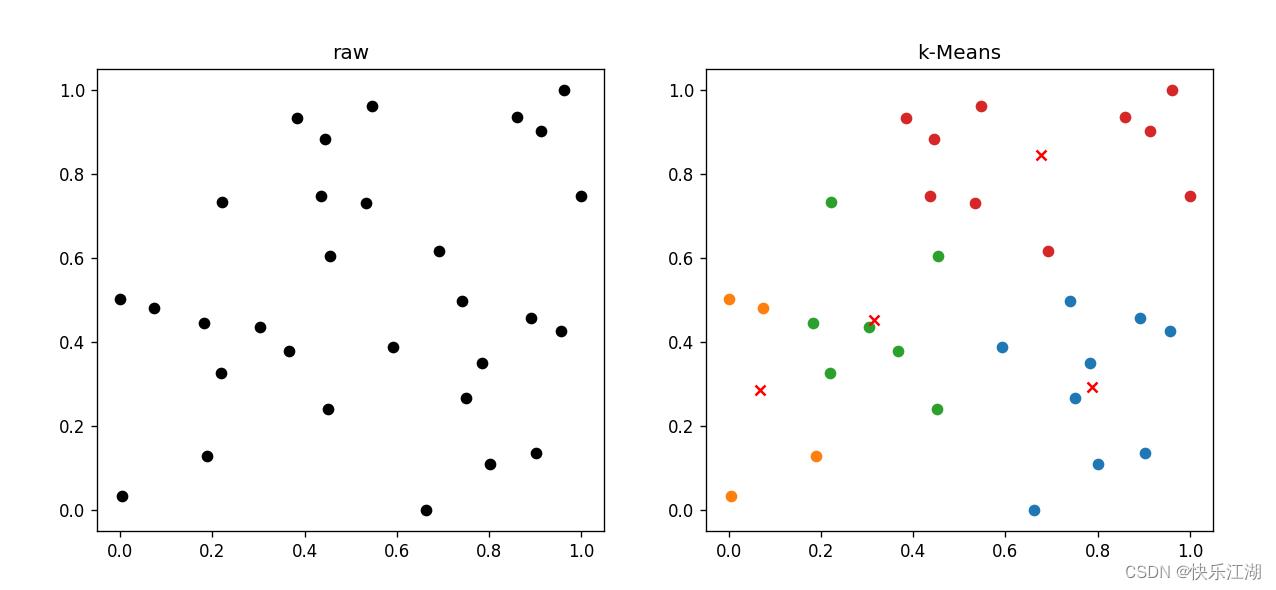
(5)Spril数据集(差)
- 代码同(2)
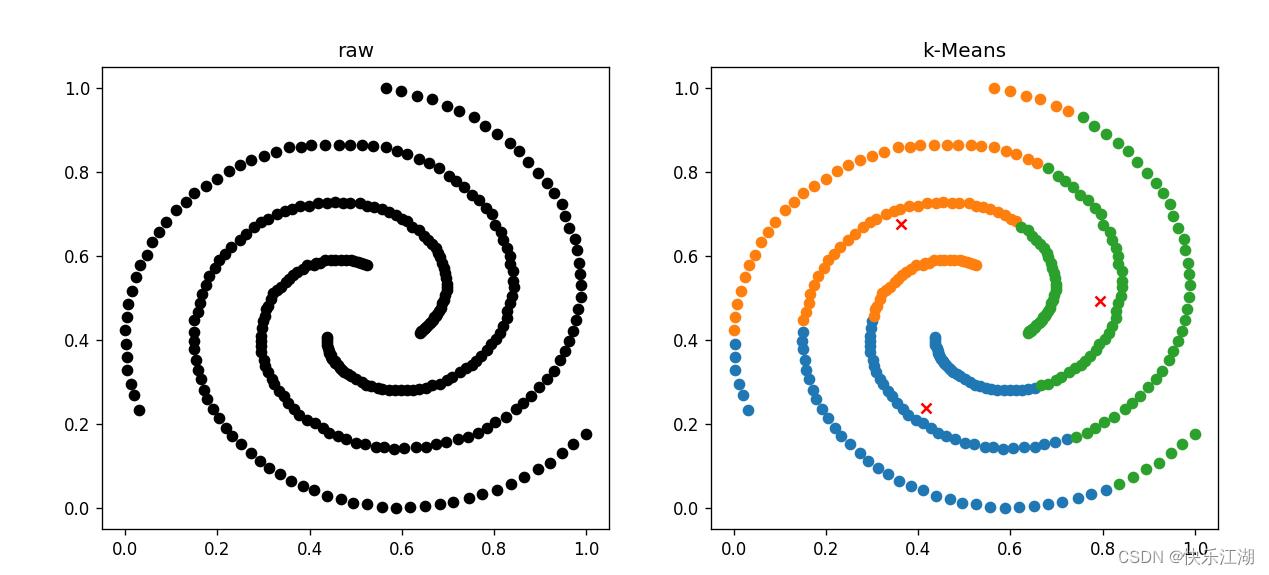
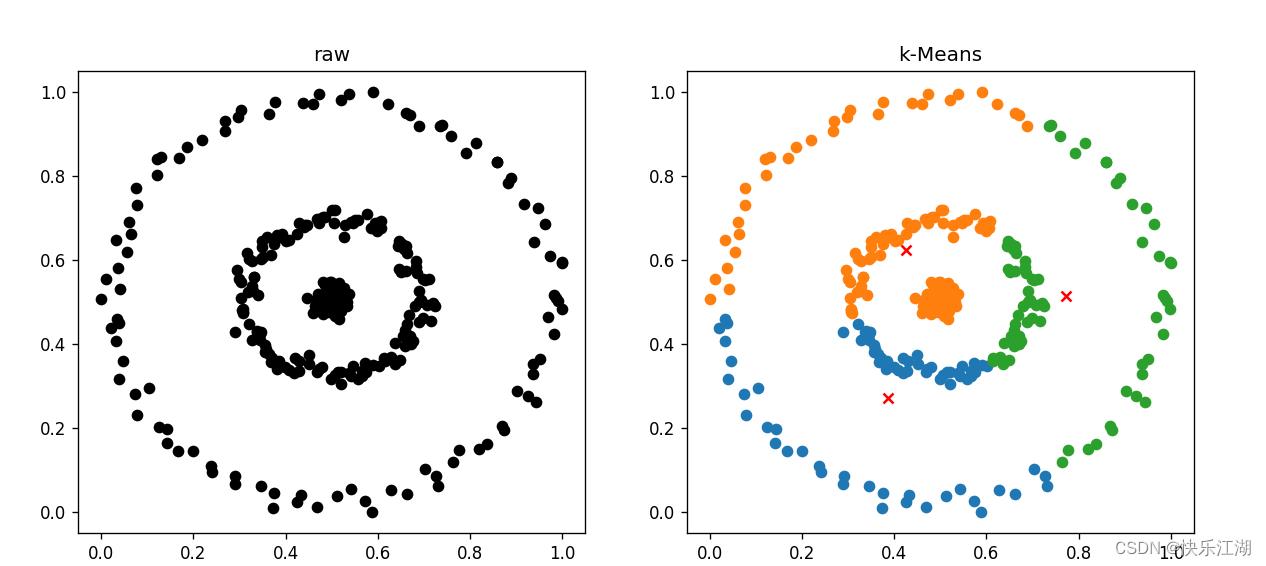
(6)threeCircles数据集(差)
- 代码同(2)
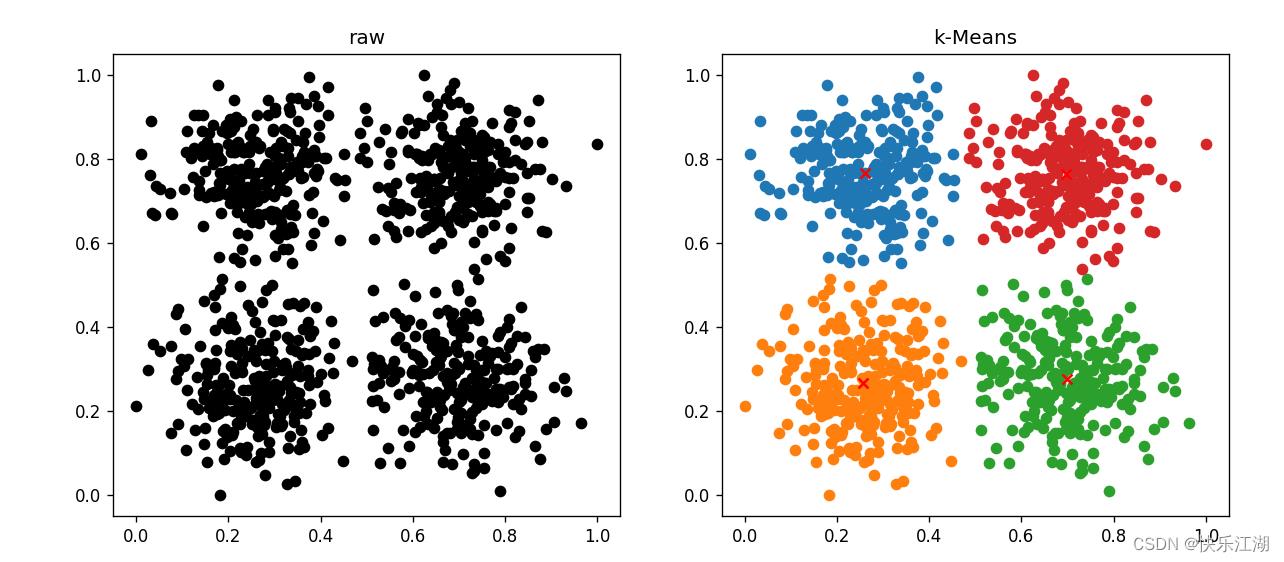
(7)Square数据集(好)
- 代码同(2)
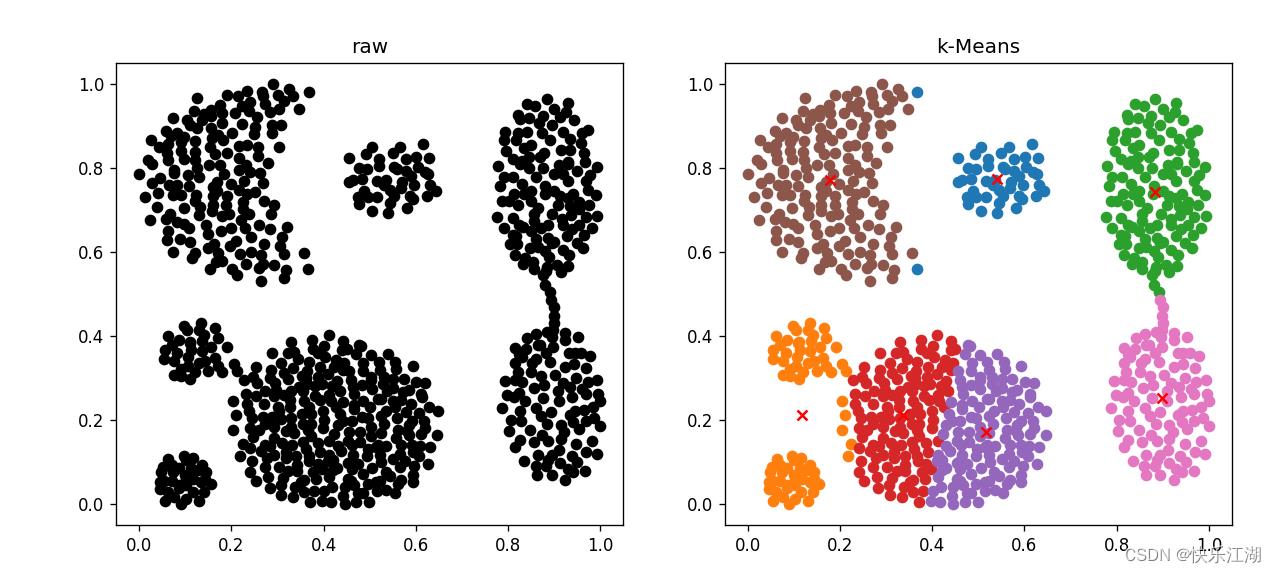
(8)lineblobs数据集(差)

(9)788points数据集(差)
- 代码同(2)
(10)gassian数据集(好)
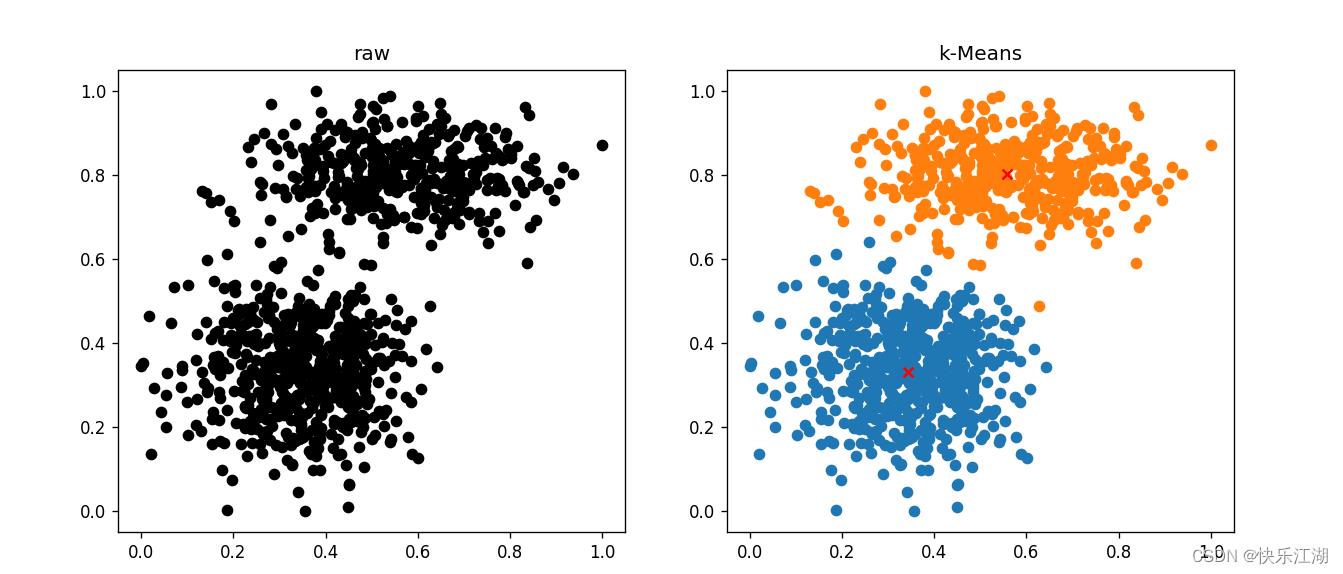
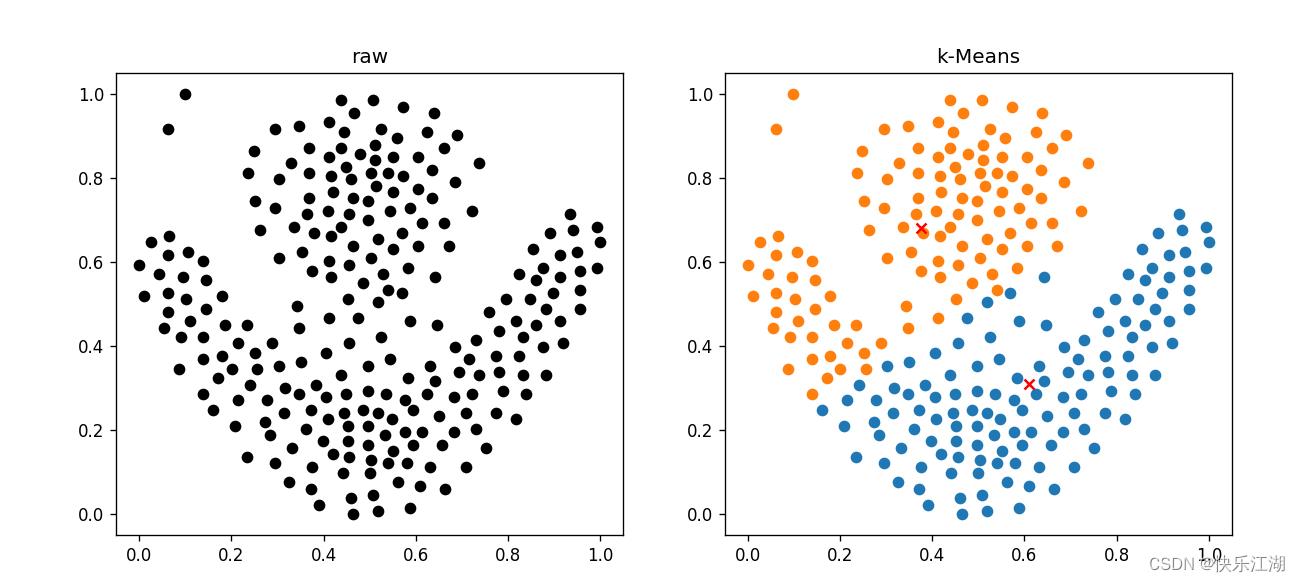
(11)arrevation数据集(较差)
以上是关于第二节2:K-Means算法及其Python实现(算法实现结果展示)的主要内容,如果未能解决你的问题,请参考以下文章