无约束优化算法-第二节:梯度类算法
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了无约束优化算法-第二节:梯度类算法相关的知识,希望对你有一定的参考价值。
文章目录
梯度类算法:梯度类算法本质是使用函数的一阶导数信息选取下降方向 d k d^k dk,这其中最基本的算法是梯度下降法,也即直接选择负梯度作为下降方向 d k d^k dk,此外还有BB方法,是一种梯度法的变形,虽然理论性质目前仍不完整,但由于它有优秀的数值表现,也是在实际应用中使用较多的一种算法
一:梯度下降法
(1)梯度下降法概述
梯度下降法(Gradient descent,GD):使用梯度下降法寻找函数极小值时,会沿着当前点对应梯度(或近似梯度)的反方向 d d d所规定的步长 α \\alpha α内进行迭代搜索。当然如果沿着梯度正方向搜索,就会接近函数的局部最大值,此时对应梯度上升法
我们经常会用下山这个例子来理解梯度下降法:现在你可以想象自己站在一座高山上的某一位置,需要下山,那么此时最快的下山策略就是环顾四周、哪里最陡峭就沿着哪个方向下山,每到一个新的地方后再次执行这个策略
- 在机器学习中,上面的初始位置就相当于损失函数的初始值,山体的陡峭程度则是梯度,对应于损失函数的导数后偏导数
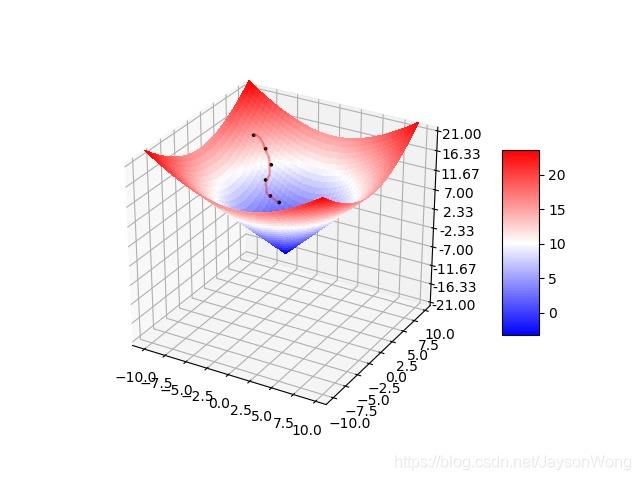
可以看出梯度下降有时得到的是局部最优解,如果损失函数是凸函数,梯度下降法得到的解就是全局最优解
因此,梯度下降法公式为
θ i = θ i − α ∂ J ( θ 0 , θ 1 , . . . , θ n ) ∂ θ i \\theta_i=\\theta_i-\\alpha \\frac\\partial J(\\theta_0,\\theta_1,...,\\theta_n)\\partial \\theta_i θi=θi−α∂θi∂J(θ0,θ1,...,θn)

(2)梯度下降法求解步骤
梯度下降法求解步骤:如下
- 确定当前位置的损失函数梯度,对于 θ i \\theta_i θi,其梯度表达式为 ∂ J ( θ 0 , θ 1 , . . . , θ n ) ∂ θ i \\frac\\partial J(\\theta_0,\\theta_1,...,\\theta_n)\\partial \\theta_i ∂θi∂J(θ0,θ1,...,θn)
- 用步长乘以损失函数梯度,得到当前位置下降的距离,也即 α ∂ J ( θ 0 , θ 1 , . . . , θ n ) ∂ θ i \\alpha \\frac\\partial J(\\theta_0,\\theta_1,...,\\theta_n)\\partial \\theta_i α∂θi∂J(θ0,θ1,...,θn)
- 确定是否所有的 θ i \\theta_i θi梯度下降的距离都小于 ξ \\xi ξ,如果小于则算法终止,当前所有的 θ i \\theta_i θi即为最终结果。否则转入下一步
- 更新所有的 θ i \\theta_i θi,即 θ i = θ i − α ∂ J ( θ 0 , θ 1 , . . . , θ n ) ∂ θ i \\theta_i=\\theta_i-\\alpha \\frac\\partial J(\\theta_0,\\theta_1,...,\\theta_n)\\partial \\theta_i θi=θi−α∂θi∂J(θ0,θ1,...,θn),更新完毕后转入第一步
(3)Python实现
- 注意: a l p h a alpha alpha的选择可以参照前文,这里固定 a l p h a alpha alpha为0.01
import numpy as np
import torch
from sympy import *
# 计算梯度函数
def cal_grad_funciton(function):
res = []
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
for i in range(len(x)):
res.append(diff(function, x[i]))
return res
# 定义目标函数
def function_define():
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
# y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
# Rosenbrock函数
y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
return y
# 计算函数返回值
def cal_function_ret(function, x):
res = function.subs([('x1', x[0]), ('x2', x[1])])
return res
# 计算梯度
def cal_grad_ret(grad_function, x):
res = []
for i in range(len(x)):
res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
return res
def norm(x):
return sqrt(np.dot(x, x))
def gradient_descent(function, grad_function, x):
k = 1
d = cal_grad_ret(grad_function, x)
d = np.dot(-1, d).tolist()
alpha = 0.01
while norm(d) > 0.00001 and k < 1000:
d = cal_grad_ret(grad_function, x)
d = np.dot(-1, d).tolist()
# armijo_goladstein准则选择步长
# alpha = armijo_goldstein(function, grad_function, x, d)
# armijo_wlofe准则选择步长
# alpha = armijo_wlofe(function, grad_function, x, d)
x = np.add(x, np.dot(alpha, d))
k = k + 1
# 返回最小值点,函数最小值和迭代次数
return x, cal_function_ret(function, x), k
if __name__ == '__main__':
function = function_define()
grad_function = cal_grad_funciton(function)
print("函数为:", function)
print("梯度函数为:", grad_function)
x0 = [-10, 10]
Min, MinValue, Iterator = gradient_descent(function, grad_function, x0)
print("最小值点为:", Min)
print("最小值为:", MinValue)
print("迭代次数为:", Iterator)

(4)常见梯度下降算法
A:全梯度下降算法(FGD)
全梯度下降算法(FGD):计算训练集所有样本误差,对其求和再取平均值作为目标函数。权重向量沿其梯度相反的方向移动,从而使当前目标函数减少得最多。因为在执行每次更新时,需要在整个数据集上计算所有的梯度,所以速度会很慢,同时,其在整个训练数据集上计算损失函数关于参数θ的梯度
θ = θ − η ⋅ ∇ θ J ( θ ) \\theta = \\theta -\\eta \\cdot \\nabla_\\thetaJ(\\theta) θ=θ−η⋅∇θJ(θ)
B:随机梯度下降算法(SGD)
随机梯度下降算法(SGD):由于FGD每迭代更新一次权重都需要计算所有样本误差,而实际问题中经常有上亿的训练样本,故效率偏低,且容易陷入局部最优解,因此提出了随机梯度下降算法。其每轮计算的目标函数不再是全体样本误差,而仅是单个样本误差,即每次只代入计算一个样本目标函数的梯度来更新权重,再取下一个样本重复此过程,直到损失函数值停止下降或损失函数值小于某个设定的阈值。此过程简单,高效,通常可以较好地避免更新迭代收敛到局部最优解。其迭代形式为
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i ) ; y ( i ) ) \\theta = \\theta -\\eta \\cdot \\nabla_\\thetaJ(\\theta;x^(i);y^(i)) θ=θ−η⋅∇θJ(θ;x(i);y(i))
- x ( i ) x^(i) x(i):表示一条训练样本的特征值
- x ( i ) x^(i) x(i):表示一条训练样本的标签值
C:小批量梯度下降算法
小批量梯度下降算法:小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。每次从训练样本集上随机抽取一个小样本集,在抽出来的小样本集上采用FGD迭代更新权重。被抽出的小样本集所含样本点的个数称为batch_size,通常设置为2的幂次方,更有利于GPU加速处理
batch_size=1,则变成了SGDbatch_size=n,则变成了FGD
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i : i + n ) ; y ( i : i + n ) ) \\theta = \\theta -\\eta \\cdot \\nabla_\\thetaJ(\\theta;x^(i:i+n);y^(i:i+n)) θ=θ−η⋅无约束优化算法-第三节:次梯度类算法