无约束优化问题
Posted oliveQ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了无约束优化问题相关的知识,希望对你有一定的参考价值。
无约束优化问题
无约束优化问题
无约束优化问题属于限制比较少,适合通过技巧来简化求解过程
基本形式
min f ( ( x ) , f ( x ) : R n → R \\minf((x),f(x):R^n\\rightarrow R minf((x),f(x):Rn→R
假设: 1. f ( x ) 是 凸 函 数 2. f ( x ) 二 阶 可 导 3. 存 在 唯 一 的 优 化 点 x ∗ , 有 p ∗ = inf x f ( x ) 1.f(x)是凸函数\\quad 2.f(x)二阶可导\\quad 3.存在唯一的优化点x^*,有p^*=\\inf_xf(x) 1.f(x)是凸函数2.f(x)二阶可导3.存在唯一的优化点x∗,有p∗=infxf(x)
注意: x ∗ o p t i m a l ⟺ ∇ f ( x ∗ ) = 0 x^* optimal\\iff \\nablaf(x^*)=0 x∗optimal⟺∇f(x∗)=0
例子
-
二次规划问题: min 1 2 x T P x + q T x + r , P ∈ S + n , q ∈ R n , r ∈ R \\min\\frac12x^TPx+q^Tx+r,P\\isin S_+^n,q\\isin R^n,r\\isin R min21xTPx+qTx+r,P∈S+n,q∈Rn,r∈R
对f(x)求导得到 p x + q = 0 px+q=0 px+q=0-
P ∈ S + + n P\\isin S_++^n P∈S++n: 有唯一解
-
P ∈ S + n P\\isin S_+^n P∈S+n: 无穷多组解
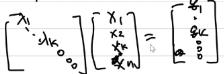
-
P ∈ S + n , q 含 有 非 零 元 素 使 得 等 式 不 成 立 P\\isin S_+^n,q含有非零元素使得等式不成立 P∈S+n,q含有非零元素使得等式不成立: 无解
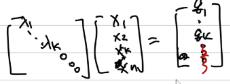
-
-
几何规划问题: d o m f = R n , f ( x ) = log ( ∑ i = 1 m exp ( a i T x + b i ) ) domf=R^n, f(x)=\\log(\\sum\\limits_i=1^m\\exp(a_i^Tx+b_i)) domf=Rn,f(x)=log(i=1∑mexp(aiTx+bi))
求导得到: ∇ f = ∑ exp ( a i T x + b i ) a i ( ∑ exp ( a i T x + b i ) ) \\nabla f=\\frac\\sum\\exp(a_i^Tx+b_i)a_i(\\sum\\exp(a_i^Tx+b_i)) ∇f=(∑exp(aiTx+bi))∑exp(aiTx+bi)ai, 这是一个超越方程,难以求解
-
类似的问题: d o m f = x ∣ a i T x < b i , ∀ i , f ( x ) = − ∑ i = 1 m log ( b i − a i T x ) domf=\\x|a_i^Tx<b_i,\\foralli\\,f(x)=-\\sum\\limits_i=1^m\\log(b_i-a_i^Tx) domf=x∣aiTx<bi,∀i,f(x)=−i=1∑mlog(bi−aiTx)
求导得到: ∇ f = ∑ a i b i − a i T x \\nablaf=\\sum\\fraca_ib_i-a_i^Tx ∇f=∑bi−aiTxai, 依然非常难解
强凸性质
-
定义[最小的特征值也大于m],以下的推导假设具有强凸性质
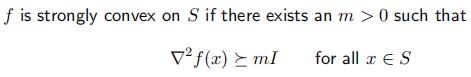
-
对f(y)做泰勒展开,设存在 z ∈ [ x , y ] z\\isin[x,y] z∈[x,y]使得泰勒展开成立
f ( y ) = f ( x ) + ∇ T f ( x ) ( y − x ) + 1 2 ( y − x ) T ∇ 2 f ( z ) ( y − x ) f(y)=f(x)+\\nabla^Tf(x)(y-x)+\\frac12(y-x)^T\\nabla^2f(z)(y-x) f(y)=f(x)+∇Tf(x)(y−x)+21(y−x)T∇2f(z)(y−x)
因为 ∇ 2 f ( x ) ≥ m I \\nabla^2f(x)\\geq mI ∇2f(x)≥mI
-
所以 f ( y ) ≥ f ( y ~ ) = f ( x ) + ∇ f ( x ) T ( y ~ − x ) + m 2 ∣ ∣ y ~ − x ∣ ∣
以上是关于无约束优化问题的主要内容,如果未能解决你的问题,请参考以下文章