聚类算法K-Means算法及其Python实现

Posted 2022-05-18 快乐江湖

文章目录

• 一：无监督学习
• • （1）什么是无监督学习
  • （2）聚类和分类
• 二：K-Means算法
• • （1）算法简介
  • （2）算法流程
  • （3）Python实现
  • （4）聚类效果展示
  • • A：鸢尾花数据集（效果好）
    • B：三个圆圈数据集（效果差）
• 三：K-Means算法探讨
• • （1）距离度量
  • （2）聚类算法评价指标
  • • A：inertia（簇内平方和）
    • B：轮廓系数
    • C： Calinski-Harabasz指数

一：无监督学习

K-Means算法是一种无监督的聚类算法

（1）什么是无监督学习

无监督学习：对于数据集，在训练的过程中，并没有告诉训练算法某一个数据应该属于哪一个类别；它是通过某种操作，将一堆“相似”的数据聚集在一起然后当做一个类别

• 例如图像分割，计算机面对图像数据时，并不认为这些数据有什么区别。但是通过聚类算法就可以实现简单的分类实现分割

（2）聚类和分类

分类和聚类是两类不同的机器学习算法， 简单来说

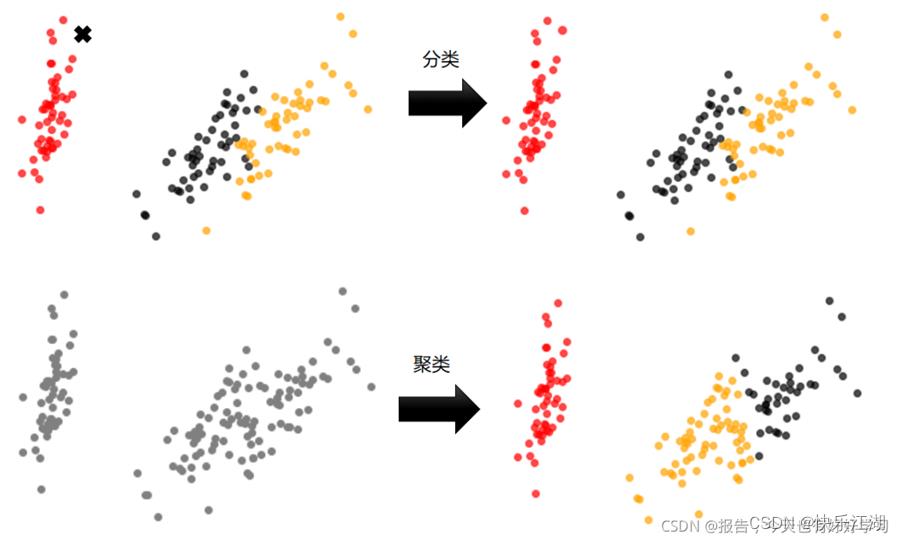
• 分类：根据文本的特征或属性，划分到已有的类别中；因此这些类别是已知的
• 聚类：分析时并不知道数据会分为几类，而是通过聚类算法进行归类

二：K-Means算法

（1）算法简介

专业解释：对于给定的样本集合$D=x_1,x_2,...,x_N$，K-Means算法针对聚类所得到的簇为$C=C_1,C_2,...,C_k$，则划分的最小化平方误差为：

$$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$

其中${\mu }_i=\frac{1}{|C_i|}$$\sum _{x\in C_i}x$,如果$E$越小则表示数据集样本相似度越高

---

通俗解释：K-Means算法将一组$N$个样本划分为$K$个无交集的 簇，簇中所有数据的均值称为这个簇的 质心

• 簇：是聚类的结果表现，一个簇中的数据就认为是同一类
• 质心：簇中所有数据的均值

在该算法中，簇个数$K$是一个超参数，在算法开始前需要人为确定

• 以图像分割为例，意思就是你认为这个图像大概可以分为多少块，$K$就设置为多少

因此，K-Means 的核心任务就是根据我们设定好的 K，找出 K 个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去

聚类算法认为，被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，因此K-Means以及其他的聚类算法所追求的目标就是 簇内差异小、簇外差异大，而这个差异由 样本点到其所在簇的质心的距离来衡量，对一个簇来说，所有样本点到质心的距离之和越小，就认为这个簇中的样本越相似，差异性也越小

K-Means算法在衡量距离时，大多会采用欧氏距离

$$d(x,\mu )=\sqrt{\sum _{i=1}^n(x_i-{\mu }_i{)}^2}$$

其中

• $x$表示簇中的每个样本点
• $\mu$表示该簇的质心
• $n$表示每个样本点中的特征数目
• $i$表示组成点$x$的每个特征编号

（2）算法流程

K-Means算法流程：

1. 选择初始化的$k$个样本作为初始聚类中心，即$\mu ={\mu }_1,{\mu }_2,...,{\mu }_k$
2. 针对数据集中每个样本$x_i$，计算它到$k$个聚类中心的距离并将其分配到距离最小的聚类中心所对应的类中
3. 针对每个类别${\mu }_j$，重新计算属于该类的所有样本的质心：${\mu }_j=\frac{1}{|C_i|}$$\sum _{x\in C_i}x$
4. 重复步骤2、3，知道到达某个中止条件（比如达到某个设定的迭代次数或者小于某个误差值等等）

---

K-Means算法流程演示：

1：假设有如下数据集，随机选取$k$个点（$k$=3，红绿蓝）

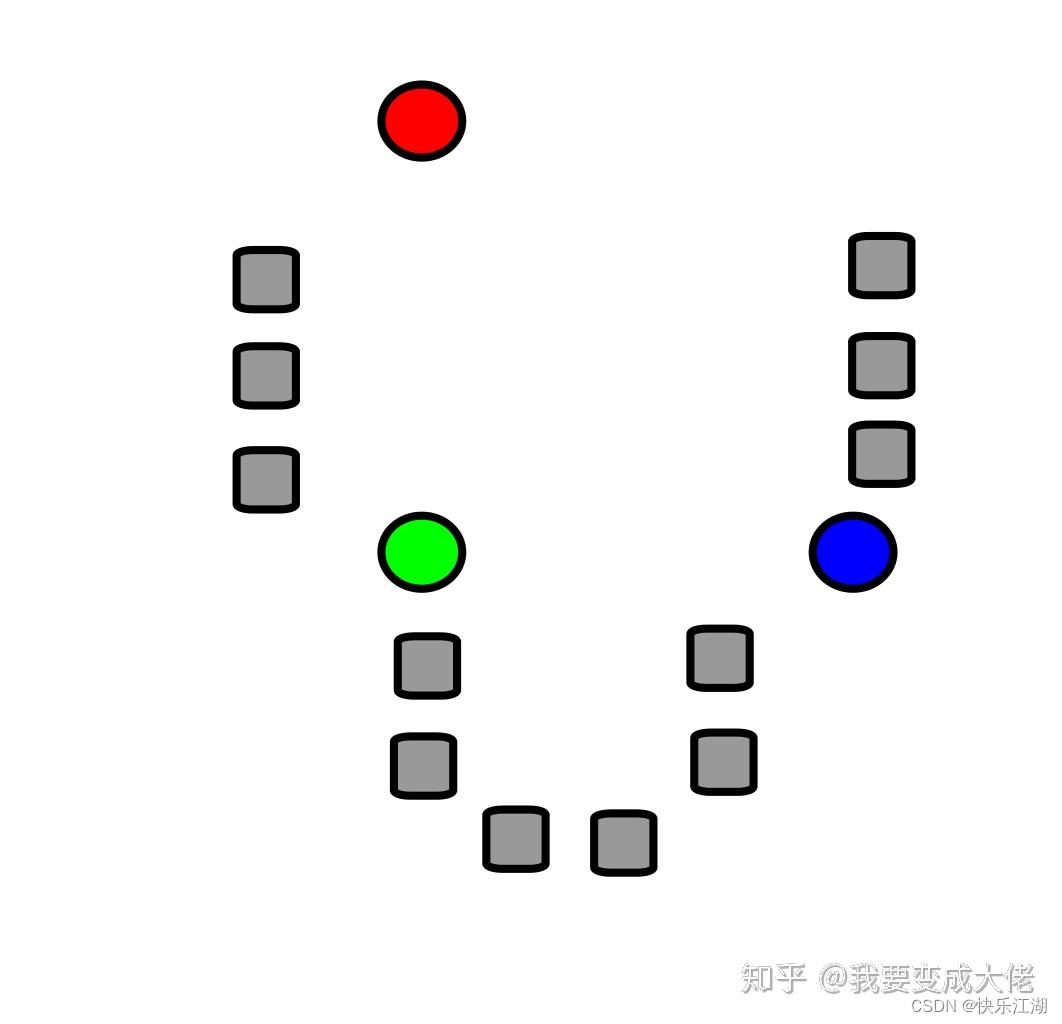
2：接着计算数据集样本中其它的点到质心的距离，然后选取最近质心的类别作为自己的类别

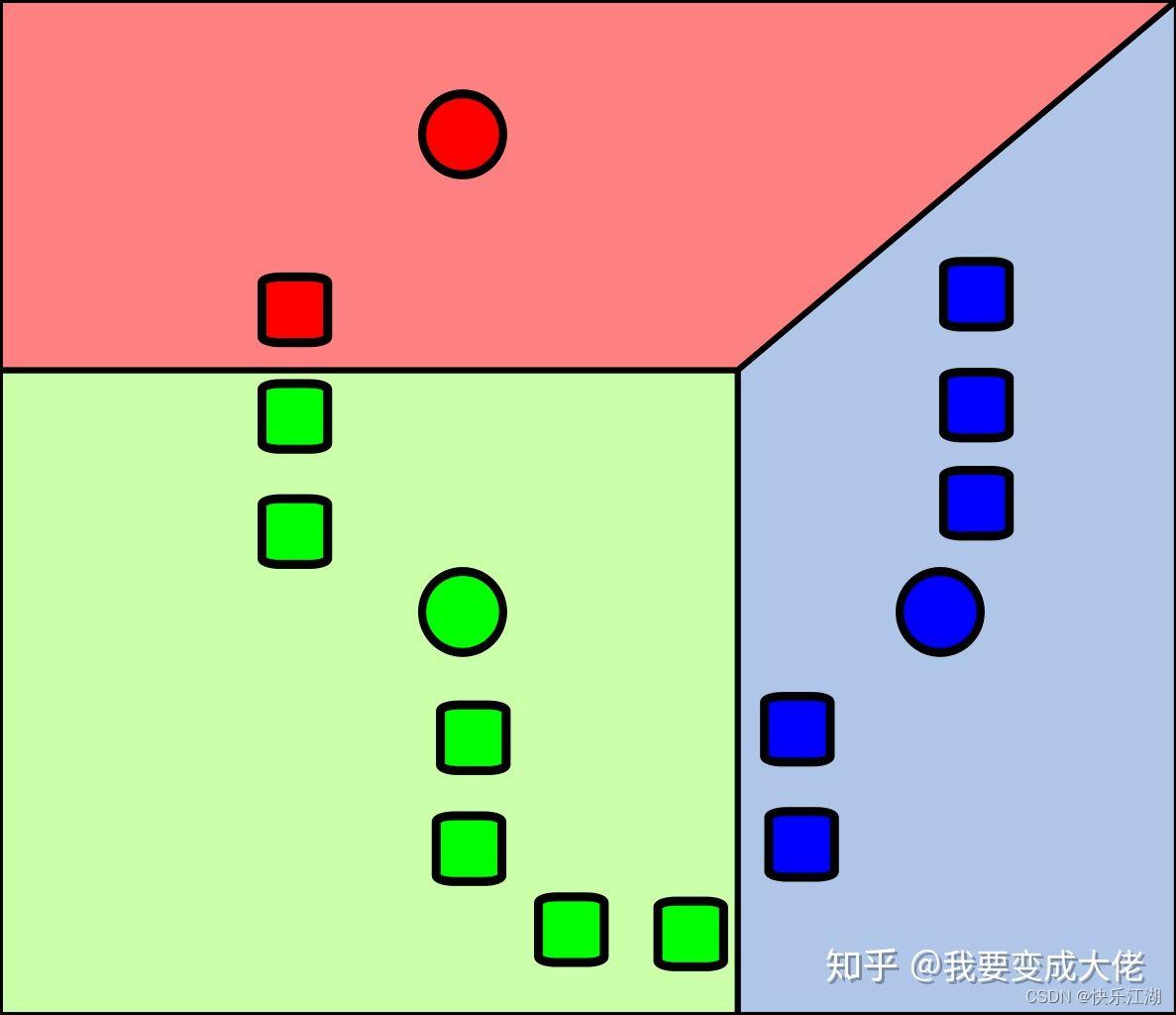
3：经过上面的步骤，分为了三个簇，然后在每个簇中重新选取质心

4：然后再进行划分

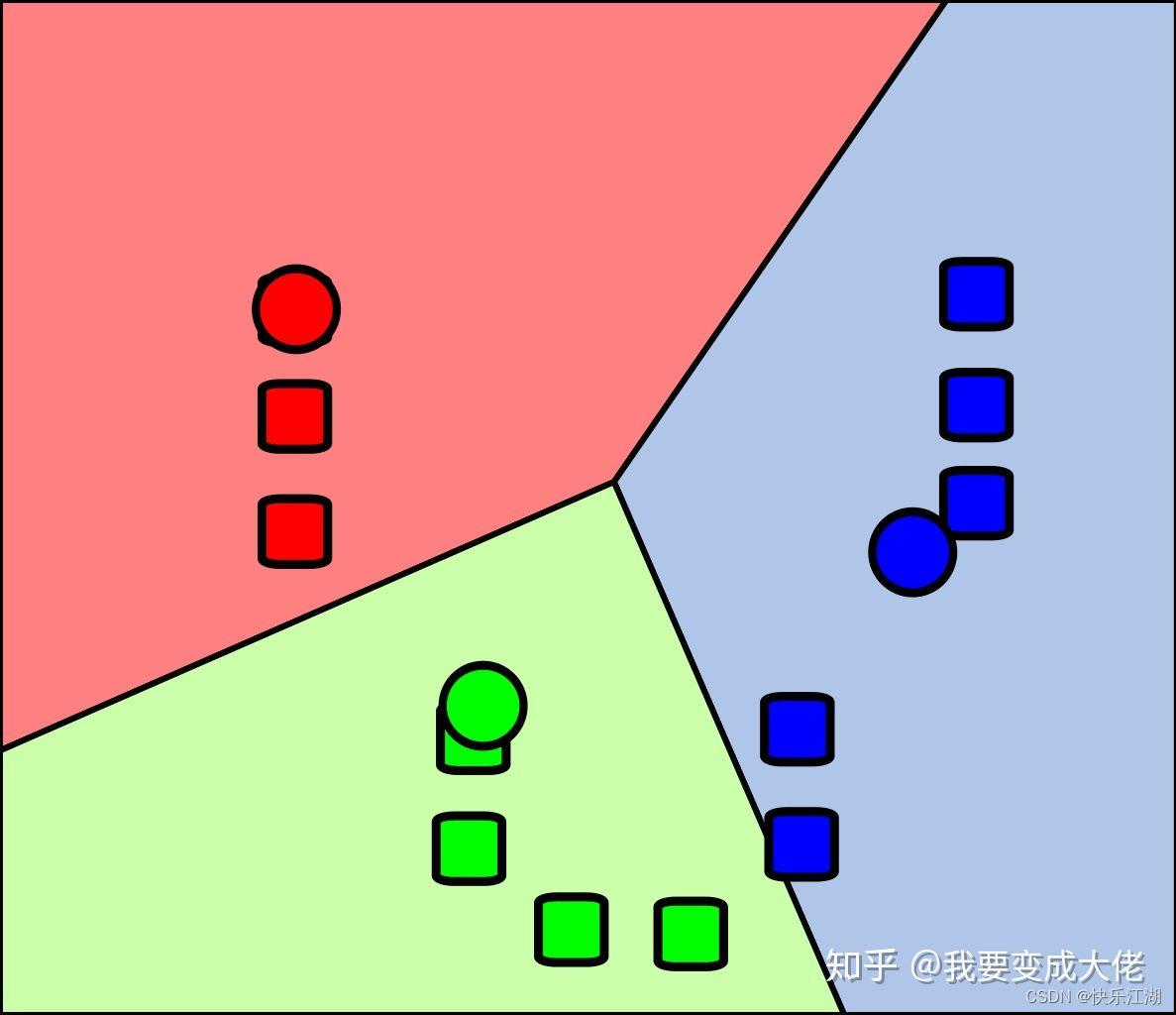
5：重复

（3）Python实现

KMeans.py：K-Means的代码实现

import numpy as np

class KMeans:
    def __init__(self, data_set, k):  # data_set：数据集  k：簇个数
        self.data_set = data_set
        self.k = k

    def kmeans(self, max_iterations):  # max_iterations：最大迭代次数
        examples_num = self.data_set.shape[0]  # 样本数据个数
        centroids = KMeans.centroids_init(self.data_set, self.k)  # 随机初始化k个质心
        closest_centroids_ids = np.empty((examples_num, 1))  # 用于保存各样本点距离哪个质心最近，例如closest_centroids_ids[0]=2表示0这个样本点和2这个执行离得最近

        #  不断迭代
        for _ in range(max_iterations):

            # 先计算各样本点到质心最短距离
            closest_centroids_ids = KMeans.centroids_find_closet(self.data_set, centroids)
            # 再更新质心
            centroids = KMeans.centroids_compute(self.data_set, closest_centroids_ids, self.k)
        return centroids, closest_centroids_ids

    @staticmethod
    def centroids_init(data_set, k):  # 初始化随机质心
        examples_num = data_set.shape[0]  # 样本数据个数
        random_ids = np.random.permutation(examples_num)  # 随机产生examples_num个数据
        centroids = data_set[random_ids[:k], :]  # 取前k个
        return centroids

    @staticmethod
    def centroids_find_closet(data_set, centroids):  # 每个样本点到质心距离
        examples_num = data_set.shape[0]  # 样本数据个数
        centroids_num = centroids.shape[0]  # 质心个数
        closet_centroids_ids = np.zeros((examples_num, 1))
        for examples_index in range(examples_num):
            distance = np.zeros((centroids_num, 1))  # 保存examples_index这个样本点到各质心的距离
            for centrodis_index in range(centroids_num):
                #  欧氏距离
                distance_diff = data_set[examples_index, :] - centroids[centrodis_index, :]  # 某点到质心差异值
                distance[centrodis_index] = np.sqrt(np.sum(np.power(distance_diff, 2)))
            closet_centroids_ids[examples_index] = np.argmin(distance)  # examples_index距离最近的那个质心（下标）
        return closet_centroids_ids

    @staticmethod
    def centroids_compute(data_set, closest_centroids_ids, k):
        features_num = data_set.shape[1]  # 特征格式，即属性
        centroids = np.zeros((k, features_num))  # k个簇每个都要计算，且每个簇的点都有features_num个属性，所以要对应计算
        for centroid_id in range(k):
            closest_ids = closest_centroids_ids == centroid_id  # 不懂的话可以查阅“Numpy布尔数组相关内容”
            centroids[centroid_id] = np.mean(data_set[closest_ids.flatten(), :], axis=0)
        return centroids

（4）聚类效果展示

A：鸢尾花数据集（效果好）

Iris.csv 文件：鸢尾花数据集

Id,SepalLengthCm,SepalWidthCm,PetalLengthCm,PetalWidthCm,Species
1,5.1,3.5,1.4,0.2,Iris-setosa
2,4.9,3.0,1.4,0.2,Iris-setosa
3,4.7,3.2,1.3,0.2,Iris-setosa
4,4.6,3.1,1.5,0.2,Iris-setosa
5,5.0,3.6,1.4,0.2,Iris-setosa
6,5.4,3.9,1.7,0.4,Iris-setosa
7,4.6,3.4,1.4,0.3,Iris-setosa
8,5.0,3.4,1.5,0.2,Iris-setosa
9,4.4,2.9,1.4,0.2,Iris-setosa
10,4.9,3.1,1.5,0.1,Iris-setosa
11,5.4,3.7,1.5,0.2,Iris-setosa
12,4.8,3.4,1.6,0.2,Iris-setosa
13,4.8,3.0,1.4,0.1,Iris-setosa
14,4.3,3.0,1.1,0.1,Iris-setosa
人工智能算法——K均值聚类算法Python实现

 基于K-Means聚类算法的主颜色提取
 Kmeans聚类算法及其 Python实现
 Kmeans 聚类 及其python实现
 k-means聚类算法
 机器学习 - 算法 - 聚类 K-MEANS 算法