:函数极限连续:第一节:函数
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了:函数极限连续:第一节:函数相关的知识,希望对你有一定的参考价值。
文章目录
高等数学主要内容有
- 函数、极限、连续
- 导数与微分
- 微分中值定理
- 不定积分
- 定积分与反常积分
- 定积分应用
- 微分方程
- 多元微分及其应用
- 二重积分
- 无穷级数
- 空间解析几何及其应用
- 三重积分和线面积分
高等数学和微积分的关系
总的来说,高等数学包括微积分,其核心内容是微积分
- 文史科各类专业的学生,学的数学稍微浅一些,课本常称“微积分”
- 理工科各类专业的学生,学的数学较难,课本常称“高等数学"
而微积分主要研究微分学和积分学
- 微分学:研究函数的导数与微分及其在函数研究中的应用
- 积分学:研究对象也是函数,其研究方法是另一类极限值的计算,牵涉到曲边形面积和体积的计算,其研究任务是积分的性质、法则和应用
对于微积分,它研究的核心内容就是 变化,因为这时间万事万物都处在变化之中,唯一不变的就是变化,具体来说就是事物运动中的数量变化规律
一:函数概念及常见函数
(1)函数的基本概念
定义:设
x
x
x和
y
y
y是两个变量,
D
D
D是一个给定的数集。如果对于每个数
x
∈
D
x\\in D
x∈D,变量
x
x
x按照一定的法则总有一个确定的数值
y
y
y与之对应,则称
y
y
y是
x
x
x的函数,并记为
y
=
f
(
x
)
,
x
∈
D
y=f(x),x \\in D
y=f(x),x∈D
其中
- x x x称为自变量, y y y称为因变量
- D D D称为该函数的定义域,记作 D f D_f Df,也即 D f = D D_f=D Df=D
- 函数值 f ( x ) f(x) f(x)的全体所构成的集合称为函数的值域,记作 R f R_f Rf或 f ( D ) f(D) f(D),即 R f = f ( D ) = y ∣ y = f ( x ) , x ∈ D R_f=f(D)=\\y | y=f(x),x\\in D\\ Rf=f(D)=y∣y=f(x),x∈D
因此,一个函数有两个基本要素,分别为
- 定义域
- 对应法则
(2)复合函数
定义:设函数 y = f ( u ) y=f(u) y=f(u)的定义域为 D f D_f Df,函数 u = g ( x ) u=g(x) u=g(x)的定义域为 D g D_g Dg,值域为 R g R_g Rg,若 D f ∩ R g ≠ ∅ D_f \\cap R_g \\neq \\emptyset Df∩Rg=∅,则称函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]为函数 y = f ( u ) y=f(u) y=f(u)与 u = g ( x ) u=g(x) u=g(x)的复合函数,其定义域为 x ∣ x ∈ D g , g ( x ) ∈ D f \\x|x\\in D_g,g(x)\\in D_f\\ x∣x∈Dg,g(x)∈Df
- 判断两个函数是否可以复合:看内层函数的值域与外层函数的定义域是否有交集,有则可以
(3)反函数
定义:设函数 y = f ( x ) y=f(x) y=f(x)的定义域为 D D D,值域为 R y R_y Ry,若对任意 y ∈ R y y\\in R_y y∈Ry,有唯一确定的 x ∈ D x\\in D x∈D使得 y = f ( x ) y=f(x) y=f(x),则即为 x = f − 1 ( y ) x=f^-1(y) x=f−1(y),称其为函数 y = f ( x ) y=f(x) y=f(x)的反函数
- 不是每个函数都有反函数:例如 y = x 2 y=x^2 y=x2没有反函数
- 单调函数一定有反函数,但是有反函数却不一定是单调的
- 重点: f − 1 [ f ( x ) ] = x f^-1[f(x)]=x f−1[f(x)]=x、 f [ f − 1 ( x ) ] = x f[f^-1(x)]=x f[f−1(x)]=x
(4)初等函数
A:基本初等函数
将幂、指数、对数、三角和反三角函数统称为基本初等函数
- 幂函数: y = x u y=x^u y=xu( u u u为实数)
- 指数函数: y = a x y=a^x y=ax( a a a>0且 a ≠ 1 a\\neq 1 a=1)
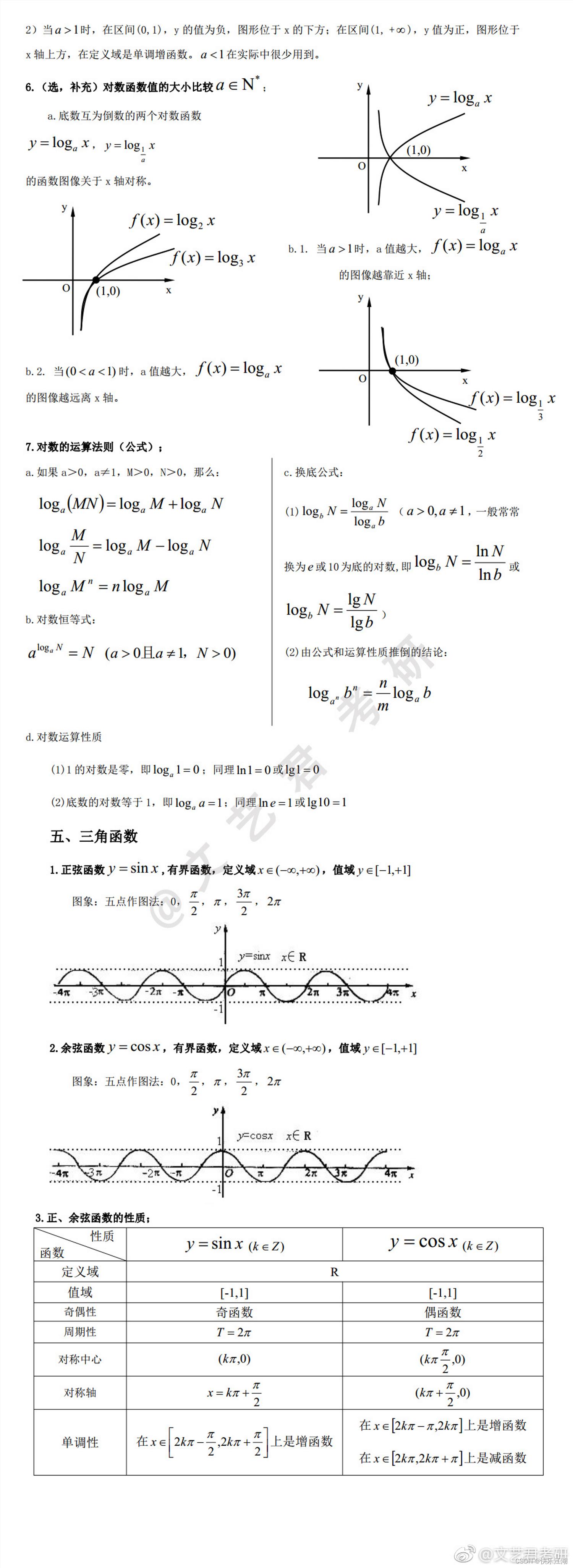
- 对数函数: y = l o g a x y=log_ax y=logax(( a a a>0且 a ≠ 1 a\\neq 1 a=1)
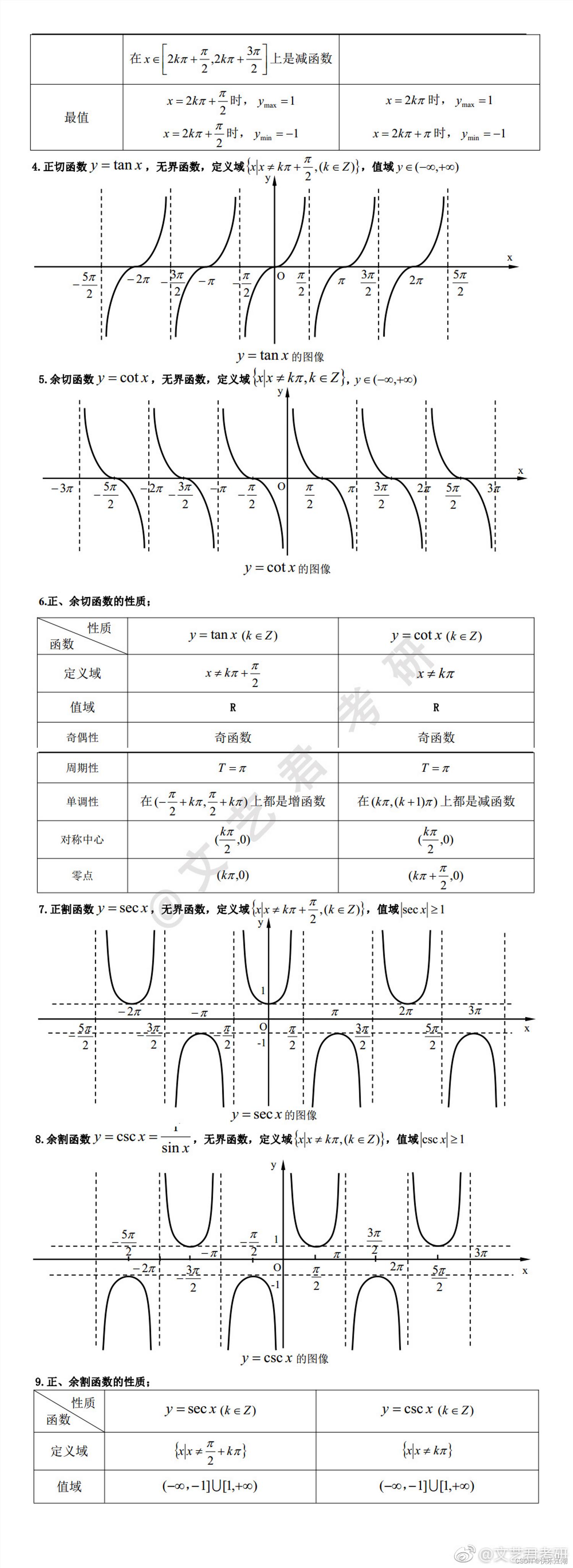
- 三角函数: y = s i n x y=sinx y=sinx 、 y = c o s x y=cosx y=cosx、 y = t a n x y=tanx y=tanx、 y = c o t x y=cotx y=cotx
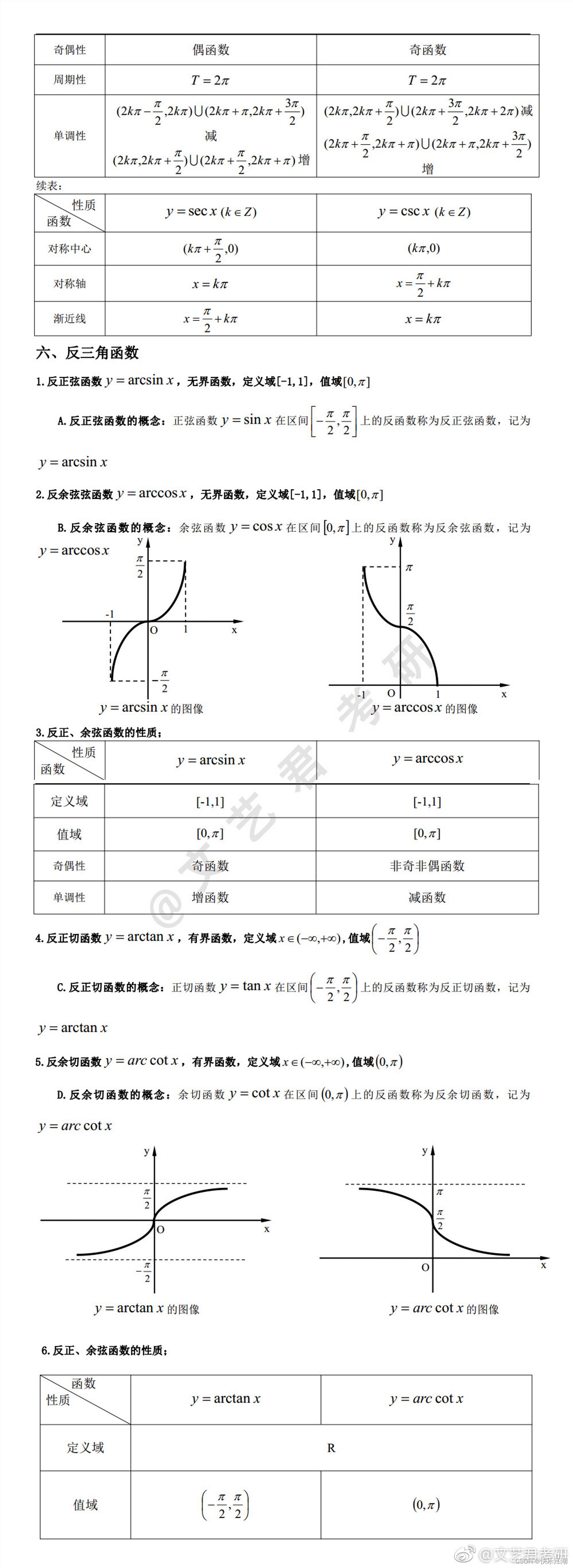
- 反三角函数: y = a r c s i n x y=arcsinx y=arcsinx 、 y = a r c c o s x y=arccosx y=arccosx、 y = a r c t a n x y=arctanx y=arctanx


B:初等函数
初等函数:定义由常数和基本初等函数经过有限次四则运算和有限次的函数复合所构成并可用一个式子表示的函数,称为初等函数
二:函数的性质
(1)单调性
定义:设函数
y
=
f
(
x
)
y=f(x)
y=f(x)在某区间
I
I
html 以上是关于:函数极限连续:第一节:函数的主要内容,如果未能解决你的问题,请参考以下文章