算法: 使用交易费买卖股票的最佳时机714. Best Time to Buy and Sell Stock with Transaction Fee

Posted 2022-03-15 AI架构师易筋

714. Best Time to Buy and Sell Stock with Transaction Fee

You are given an array prices where prices[i] is the price of a given stock on the ith day, and an integer fee representing a transaction fee.

Find the maximum profit you can achieve. You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,3,2,8,4,9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
- Buying at prices[0] = 1
- Selling at prices[3] = 8
- Buying at prices[4] = 4
- Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

Example 2:

Input: prices = [1,3,7,5,10,3], fee = 3
Output: 6

Constraints:

• 1 <= prices.length <= 5 * 10^4
• 1 <= prices[i] < 5 * 10^4
• 0 <= fee < 5 * 10^4

贪婪算法

难点在于公式minPrice = prices[i] - fee，有两种工作方式

1. 当您已经支付了开通交易的费用时，只要价格继续上涨，您将获得额外的利润，无需再次支付费用。因此，在 之后，minPrice = prices[i] - fee该行elif prices[i] > minPrice + fee变为j 是您最后一次设置最小值的位置。prices[i] > (prices[j] - fee) + fee， prices[i] > prices[j]
2. 当价格下跌时，您想关闭交易以实现到目前为止的利润，但只有在新价格低于上次价格减去费用时才这样做，或者prices[new] < prices[old] - fee，因为如果您现在关闭并转换价格，您将获得下次打开交易时支付费用。如果费用比您通过转换获得的利润要多，为什么要这样做？只需保留旧价格并等待更便宜的价格转换。

例子：
prices = [1, 3, 4, 5, 4, 8], fee = 2

1. 你是否从第 0 天到第 3 天（prices[3] - prices[0] = 4）和第 4 天获利第 5 天（prices[5] - prices[4] = 4）？
2. 还是您从第 0 天到第 5 天获利（prices[5] - prices[0] = 7）？
   因为交易fee = 2 , (4-2 + 4-2) < (7-2)，所以第二个选项更好。
   所以我们需要避免贪婪地设置 minPrice = day4 ，因为以 5 美元卖出并以 4 美元再次买入只会给我们多 1 美元的利润，但要多花 2 美元的交易费。
   仅当价格[今天] < 价格[昨天] - fee时才开始新交易。这就是我们设置minPrice = prices[i] - fee的原因

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        n = len(prices)
        if n < 2:
            return 0
        res = 0
        minPrice = prices[0]
        for i in range(1, n):
            if prices[i] < minPrice:
                minPrice = prices[i]
            elif prices[i] - minPrice > fee:
                res += prices[i] - minPrice - fee
                minPrice = prices[i] - fee
        return res

状态机解法

这个问题是对状态机逻辑的介绍。为了解决这个问题，我们可以考虑两种可能的不同存在状态：没有库存并准备购买（购买）和拥有库存并准备出售（出售）。

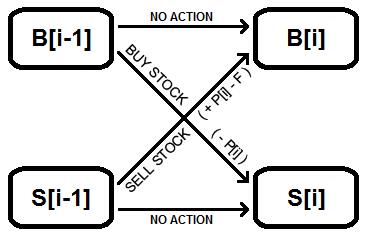
我们只需要遍历价格 ( P ) 并跟踪每天这两种状态的最佳可能值。难点在于两国的轨道经常交叉。

例如，如果我们考虑在本次迭代后准备购买股票的状态（购买），可以从今天准备购买并且什么都不做，或者可以通过今天准备出售并出售（与附加费[ F ]）。我们只需要选择能产生最佳价值的那个。

卖出状态也是如此。新的卖出状态是之前没有行动的卖出状态和之前今天买入股票的买入状态之间的更好结果。

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        buy, sell = 0, -prices[0]
        for i in range(1, len(prices)):
            buy = max(buy, sell + prices[i] - fee)
            sell = max(sell, buy - prices[i])
        return max(buy, sell)

我们应该手动设置我们购买和销售的初始值以考虑第一天并从那里迭代。

由于每个买入/​​卖出对只收取一次费用，我们可以在技术上对任何一方进行解释，因为我们总是想要返回买入状态，没有剩余的股票可供出售。

问题：在第二个等式中使用它之前，我们是否应该担心更新购买？从数学上讲，这只是买卖
的好日子；它不能两者兼而有之。

考虑可能的情况：在第一个等式中，如果旧的买入大于卖出 + P[i] - F，那么新的买入将与旧的买入相同，因此第二个等式不会发生变化。

但是，如果购买发生变化怎么办？举个例子：

  if:  buying = 10, P[i] = 4, F = 0
then:  newBuying = max(10, selling + 4 - 0)
       newSelling = max(selling, newBuying - 4)

  if:  selling <= 6                               // For values of selling less than 7
then:  newBuying = max(10, <=10)                  // the old buying will still be largest
       newBuying = buying                         // so there's no problem

  if:  selling > 6                                // If selling is greater than 6
then:  newBuying = max(10, >6 + 4)                // then buying will change
       newBuying = selling + 4                    // so we might have a problem

  if:  newBuying = selling + 4                    // But here we see that selling cannot
then:  newSelling = max(selling, selling + 4 - 4) // possibly change when buying does

F的任何正值只会降低newBuying的值，这只会使newBuying - P[i]甚至无法与卖出挂钩，但总是会更低。

参考

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/discuss/201603/Python.-Greedy-is-good.

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/discuss/1112088/JS-Python-Java-C%2B%2B-or-Very-Simple-State-Machine-Solution-w-Explanation