P1404 平均数（二分/斜率优化）

Posted 2021-03-26 oneman233

先说说二分的思路：

对数列中每个数字都减去当前二分的答案，然后求出前缀和，如果前缀和在某个位置加上前M个的最小值大于0，那么就可以更新答案

事实上，减去了当前二分的答案之后，就相当于在与这一段区间都为二分答案的序列互相比较了，剩下只需要维护前M个最小值即可

注意输出答案不要四舍五入，并且要乘以1000，那么就给所有数字乘上10000，最后除以10即可

代码：

#include <bits/stdc++.h>
#define int long long
#define sc(a) scanf("%lld",&a)
#define scc(a,b) scanf("%lld %lld",&a,&b)
#define sccc(a,b,c) scanf("%lld %lld %lld",&a,&b,&c)
#define scs(a) scanf("%s",a) 
#define schar(a) scanf("%c",&a)
#define pr(a) printf("%lld",a)
#define fo(i,a,b) for(int i=a;i<b;++i)
#define re(i,a,b) for(int i=a;i<=b;++i)
#define rfo(i,a,b) for(int i=a;i>b;--i)
#define rre(i,a,b) for(int i=a;i>=b;--i)
#define prn() printf("
")
#define prs() printf(" ")
#define mkp make_pair
#define pii pair<int,int>
#define pub(a) push_back(a)
#define pob() pop_back()
#define puf(a) push_front(a)
#define pof() pop_front()
#define fst first
#define snd second
#define frt front()
#define bak back()
#define mem0(a) memset(a,0,sizeof(a))
#define memmx(a) memset(a,0x3f3f,sizeof(a))
#define memmn(a) memset(a,-0x3f3f,sizeof(a))
#define debug
#define db double
#define yyes cout<<"YES"<<endl;
#define nno cout<<"NO"<<endl;
#define all(i,a) for(auto i=a.begin();i!=a.end();++i)
using namespace std;
typedef vector<int> vei;
typedef vector<pii> vep;
typedef map<int,int> mpii;
typedef map<char,int> mpci;
typedef map<string,int> mpsi;
typedef deque<int> deqi;
typedef deque<char> deqc;
typedef priority_queue<int> mxpq;
typedef priority_queue<int,vector<int>,greater<int> > mnpq;
typedef priority_queue<pii> mxpqii;
typedef priority_queue<pii,vector<pii>,greater<pii> > mnpqii;
const int maxn=500005;
const int inf=0x3f3f3f3f3f3f3f3f;
const int MOD=100000007;
const db eps=1e-10;
const db pi=3.1415926535;
int qpow(int a,int b){int tmp=a%MOD,ans=1;while(b){if(b&1){ans*=tmp,ans%=MOD;}tmp*=tmp,tmp%=MOD,b>>=1;}return ans;}
int lowbit(int x){return x&-x;}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int mmax(int a,int b,int c){return max(a,max(b,c));}
int mmin(int a,int b,int c){return min(a,min(b,c));}
void mod(int &a){a+=MOD;a%=MOD;}
bool chk(int now);
int half(int l,int r){while(l<=r){int m=(l+r)/2;if(chk(m))l=m+1;else r=m-1;}return l;}
int ll(int p){return p<<1;}
int rr(int p){return p<<1|1;}
int mm(int l,int r){return (l+r)/2;}
int lg(int x){if(x==0) return 1;return (int)log2(x)+1;}
bool smleql(db a,db b){if(a<b||fabs(a-b)<=eps)return true;return false;}
bool bigeql(db a,db b){if(a>b||fabs(a-b)<=eps)return true;return false;}
bool eql(db a,db b){if(fabs(a-b)<eps) return 1;return 0;}
db len(db a,db b,db c,db d){return sqrt((a-c)*(a-c)+(b-d)*(b-d));}
bool isp(int x){if(x==1)return false;if(x==2)return true;for(int i=2;i*i<=x;++i)if(x%i==0)return false;return true;}
inline int read(){
    char ch=getchar();int s=0,w=1;
    while(ch<48||ch>57){if(ch==‘-‘)w=-1;ch=getchar();}
    while(ch>=48&&ch<=57){s=(s<<1)+(s<<3)+ch-48;ch=getchar();}
    return s*w;
}
inline void write(int x){
    if(x<0)putchar(‘-‘),x=-x;
    if(x>9)write(x/10);
    putchar(x%10+48);
}
int gcd(int a, int b){
    if(a==0) return b;
    if(b==0) return a;
    if(!(a&1)&&!(b&1)) return gcd(a>>1,b>>1)<<1;
    else if(!(b&1)) return gcd(a,b>>1);
    else if(!(a&1)) return gcd(a>>1,b);
    else return gcd(abs(a-b),min(a,b));
}
int lcm(int x,int y){return x*y/gcd(x,y);}

int n,m,a[maxn],s[maxn];

bool chk(int now){
    int mn=inf;
    re(i,1,n){
        s[i]=s[i-1]+a[i]-now;
        if(i>=m){
            mn=min(mn,s[i-m]);
            if(s[i]>mn) return 1;
        }
    }
    return 0;
}

signed main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;
    re(i,1,n) cin>>a[i],a[i]*=10000;
    cout<<half(1,1e9)/10;
    return 0;
}

事实上本题还可以利用斜率，考虑到平均数可以写成：(s[j]-s[i-1])/(j-(i-1))的形式，其中s是前缀和

不难发现这就是两个坐标点的二维坐标，意味着我们现在要求出j-i+1>=m的最大斜率

考虑到这题不存在斜率无穷大的情况，实际处理起来还要方便许多

注意到两个步骤：删除上凸线、维护最大斜率，分别对应了出队尾和出队首

 

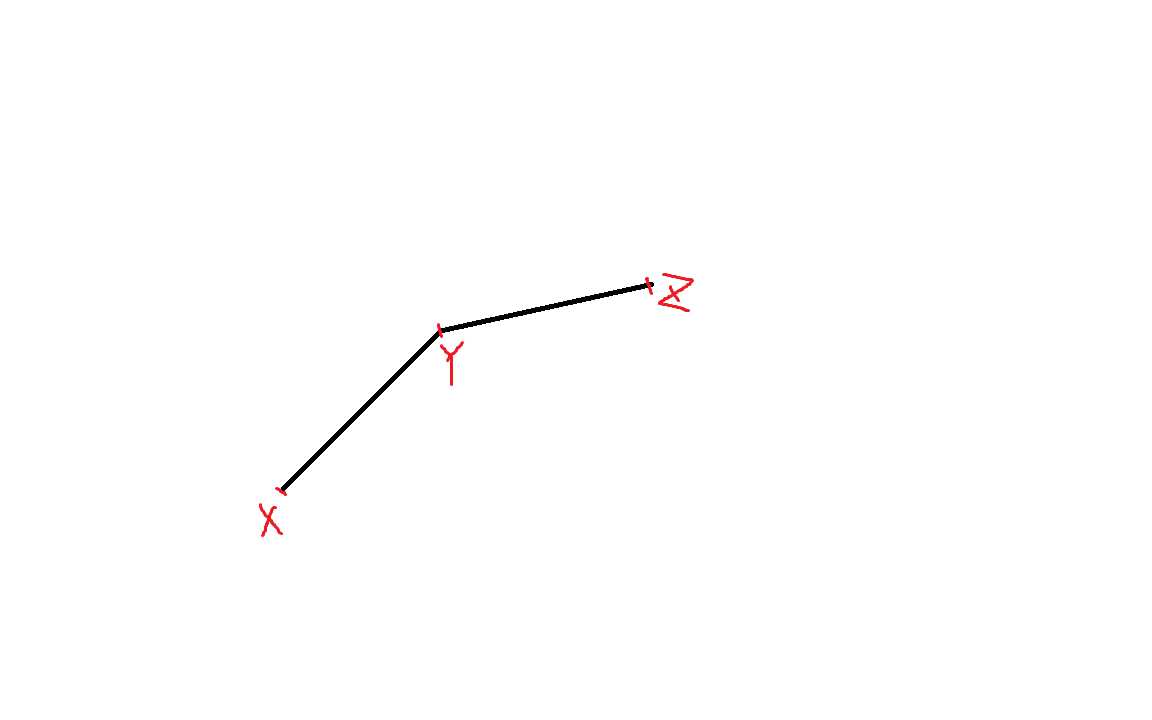
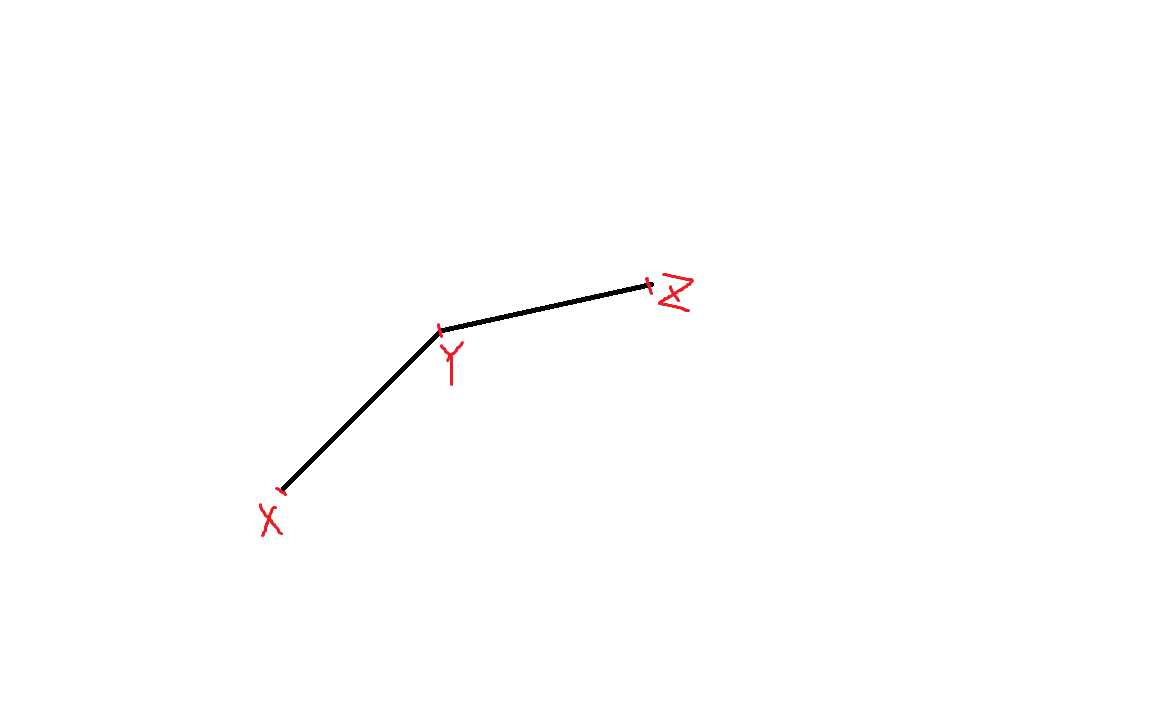
 显然发现相对于XY段，YZ一定不能起到更新答案的作用，那么就弹出YZ段。

此外每次还要不断弹出队首，直到找到最大斜率点为止。

代码：

#include <bits/stdc++.h>
#define int long long
#define sc(a) scanf("%lld",&a)
#define scc(a,b) scanf("%lld %lld",&a,&b)
#define sccc(a,b,c) scanf("%lld %lld %lld",&a,&b,&c)
#define scs(a) scanf("%s",a) 
#define schar(a) scanf("%c",&a)
#define pr(a) printf("%lld",a)
#define fo(i,a,b) for(int i=a;i<b;++i)
#define re(i,a,b) for(int i=a;i<=b;++i)
#define rfo(i,a,b) for(int i=a;i>b;--i)
#define rre(i,a,b) for(int i=a;i>=b;--i)
#define prn() printf("
")
#define prs() printf(" ")
#define mkp make_pair
#define pii pair<int,int>
#define pub(a) push_back(a)
#define pob() pop_back()
#define puf(a) push_front(a)
#define pof() pop_front()
#define fst first
#define snd second
#define frt front()
#define bak back()
#define mem0(a) memset(a,0,sizeof(a))
#define memmx(a) memset(a,0x3f3f,sizeof(a))
#define memmn(a) memset(a,-0x3f3f,sizeof(a))
#define debug
#define db double
#define yyes cout<<"YES"<<endl;
#define nno cout<<"NO"<<endl;
#define all(i,a) for(auto i=a.begin();i!=a.end();++i)
using namespace std;
typedef vector<int> vei;
typedef vector<pii> vep;
typedef map<int,int> mpii;
typedef map<char,int> mpci;
typedef map<string,int> mpsi;
typedef deque<int> deqi;
typedef deque<char> deqc;
typedef priority_queue<int> mxpq;
typedef priority_queue<int,vector<int>,greater<int> > mnpq;
typedef priority_queue<pii> mxpqii;
typedef priority_queue<pii,vector<pii>,greater<pii> > mnpqii;
const int maxn=500005;
const int inf=0x3f3f3f3f3f3f3f3f;
const int MOD=100000007;
const db eps=1e-10;
const db pi=3.1415926535;
int qpow(int a,int b){int tmp=a%MOD,ans=1;while(b){if(b&1){ans*=tmp,ans%=MOD;}tmp*=tmp,tmp%=MOD,b>>=1;}return ans;}
int lowbit(int x){return x&-x;}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int mmax(int a,int b,int c){return max(a,max(b,c));}
int mmin(int a,int b,int c){return min(a,min(b,c));}
void mod(int &a){a+=MOD;a%=MOD;}
bool chk(int now){}
int half(int l,int r){while(l<=r){int m=(l+r)/2;if(chk(m))r=m-1;else l=m+1;}return l;}
int ll(int p){return p<<1;}
int rr(int p){return p<<1|1;}
int mm(int l,int r){return (l+r)/2;}
int lg(int x){if(x==0) return 1;return (int)log2(x)+1;}
bool smleql(db a,db b){if(a<b||fabs(a-b)<=eps)return true;return false;}
bool bigeql(db a,db b){if(a>b||fabs(a-b)<=eps)return true;return false;}
bool eql(db a,db b){if(fabs(a-b)<eps) return 1;return 0;}
db len(db a,db b,db c,db d){return sqrt((a-c)*(a-c)+(b-d)*(b-d));}
bool isp(int x){if(x==1)return false;if(x==2)return true;for(int i=2;i*i<=x;++i)if(x%i==0)return false;return true;}
inline int read(){
    char ch=getchar();int s=0,w=1;
    while(ch<48||ch>57){if(ch==‘-‘)w=-1;ch=getchar();}
    while(ch>=48&&ch<=57){s=(s<<1)+(s<<3)+ch-48;ch=getchar();}
    return s*w;
}
inline void write(int x){
    if(x<0)putchar(‘-‘),x=-x;
    if(x>9)write(x/10);
    putchar(x%10+48);
}
int gcd(int a, int b){
    if(a==0) return b;
    if(b==0) return a;
    if(!(a&1)&&!(b&1)) return gcd(a>>1,b>>1)<<1;
    else if(!(b&1)) return gcd(a,b>>1);
    else if(!(a&1)) return gcd(a>>1,b);
    else return gcd(abs(a-b),min(a,b));
}
int lcm(int x,int y){return x*y/gcd(x,y);}

int n,m,a,s[maxn];
deque<int> q;

db k(int x,int y){
    return (s[y]-s[x]+0.0)/(y-x);
}

signed main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;
    re(i,1,n){
        cin>>a;
        s[i]=s[i-1]+a;
    }
    db ans=-inf;
    re(i,m,n){
        #define l q.size()
        while(l>=2&&k(i-m,q[l-1])<k(i-m,q[l-2])) q.pob();
        q.pub(i-m);
        while(l>=2&&k(i,q[0])<k(i,q[1])) q.pof();
        ans=max(ans,k(i,q.frt));
        #undef l
    }
    cout<<(int)floor(ans*1000);
    return 0;
}