B-概率论-极大似然估计

Posted 2021-03-25 nickchen121

目录

• 极大似然估计
• 一、最大似然原理
• 二、极大似然估计
• 三、似然函数
• 四、极大似然函数估计值
• 五、求解极大似然函数
  • 5.1 未知参数只有一个
  • 5.2 位置参数有多个
  • 5.3 总结

更新、更全的《机器学习》的更新网站，更有python、go、数据结构与算法、爬虫、人工智能教学等着你：https://www.cnblogs.com/nickchen121/

极大似然估计

一、最大似然原理

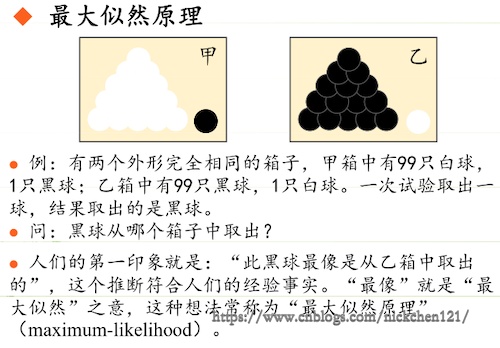
二、极大似然估计

极大似然估计是建立在最大似然原理的基础上的一个统计方法。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即“模型已定，参数未知”。通过观察若干次实验的结果，利用实验结果得到某个参数值能够使样本出现的概率最大，则称为极大似然估计。

简而言之，极大似然估计的目的是利用已知的样本结果，反推最有可能导致这样结果的参数值。

三、似然函数

假设一个样本集(D)的(n)个样本都是独立同分布的，并且该样本集为
[ D={x_1,x_2,ldots,x_n} ]
似然函数（likelihood function）：联合概率密度函数(p(D| heta))称为相对于({x_1,x_2,ldots,x_n})的( heta)的似然函数。
[ l( heta) = p(D| heta) = p(x_1,x_2,ldots,x_n| heta) = prod_{i=1}^n p(x_i| heta) ]

四、极大似然函数估计值

如果(hat{ heta})是( heta)参数空间中能使似然函数(l( heta))最大的( heta)值，则(hat{ heta})是最可能的参数值，那么(hat{ heta})是( heta)的最大似然估计量，记作
[ hat{ heta} = d(x_1,x_2,ldots,x_n) = d(D) ]
并且(hat{ heta}(x_1,x_2,ldots,x_n))称作极大似然函数估计值。

五、求解极大似然函数

给出求解最大( heta)值的公式
[ hat{ heta} = arg underbrace{max}_ heta l( heta) = arg underbrace{max}_ heta prod_{i=1}^n p(x_i| heta) ]
为了方便计算，定义对数似然函数(H( heta))，即对似然函数求对数
[ H( heta) = ln{l( heta)} ]
因此求最大( heta)值的公式变成了
[ hat{ heta} = arg underbrace{max}_ heta H( heta) = arg underbrace{max}_ heta ln{l( heta)} = arg underbrace{max}_ heta prod_{i=1}^n ln{p(x_i| heta)} ]
并且可以发现公式中只有一个变量( heta)

5.1 未知参数只有一个

如果( heta)为标量，在似然函数满足连续、可微的情况下，则极大似然估计量是下面微分方程的解
[ {frac{dH( heta)}{d heta}} = {frac{dln{l( heta)}}{d heta}} = 0 ]

5.2 位置参数有多个

如果( heta)为(k)维向量，可以把( heta)记作( heta = [ heta_1, heta_2,ldots, heta_k]^T)，对( heta_1, heta_2,ldots, heta_k)求梯度，可得
[ Delta_ heta=[{frac{partial}{partial_{ heta_1}}},{frac{partial}{partial_{ heta_2}}},cdots,{frac{partial}{partial_{ heta_s}}}]^T ]
如果似然函数满足连续、可导的情况下，则最大似然估计量就是如下方程的解：
[ Delta_ heta{H( heta)} = Delta_ hetaln{l( heta)} = sum_{i=1}^n Delta_ heta ln(p(x_i| heta)) = 0 ]

5.3 总结

方程的解只是一个估计值，只有在样本趋于无限多的时候，才会逐渐接近真实值。