树链剖分

Posted 2020-11-15 hzoi-lyl

　　

　　 树链剖分的概念：　　

　　 　　树链剖分（重链剖分），是处理树上极值、权值和问题，支持修改和查询的一种数据结构。

　　　　主体思路：1、通过轻重边剖分将树分割成多条链；

　　　　　　　　　2、再利用线段树、主席树等数据结构来维护这些链上的信息。

　　　　所以我们可以说树链剖分本质上是一种优化暴力。

 　　

　　树链剖分的要素：　

　　 　   重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；

　　　　轻儿子：父亲节点中除了重儿子以外的儿子；

 　　　   重边：父亲结点和重儿子连成的边；

　　　　轻边：父亲节点和轻儿子连成的边；

 　　　   重链：由多条重边连接而成的路径；

　　 　   轻链：由多条轻边连接而成的路径；

 　　　　

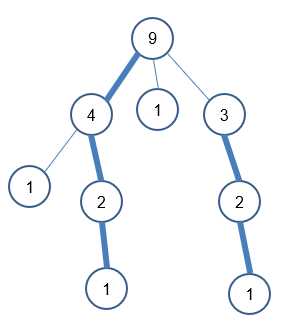
　　        如图所示：图中数字为每个节点的子树规模，粗边为重链，我们称某条路径为重链，当且仅当它全部由重边组成

　　

　　树链剖分的性质：　

　　　　1、所有重链互不相交，即每个点只属于一条重链

　　　　2、所有重链长度和等于节点数

　　　　3、一个点到根节点的路径上经过的边中轻边最多只有log条

　　　  一、二两性质由上图易得。

　　　　关于第三个性质，考虑最坏情况，令这个点到根路径上经过的边都是轻边。

　　　　那么每经过一条轻边到达这个点的父亲节点时，就代表着这个父亲节点至少还有一个与当前子树同样规模的子树，

　　　　也就是说每经过一条轻边走到的点的子树大小就要乘2，因此最多只能走log次。

　　　　第三个性质解释了为什么为什么我们选择重儿子维护树链信息的原因，也是树链剖分算法时空复杂度的保证。

　　

　　树链剖分的实现：　

　　　　　

数组名称	解释
fa[u]	保存结点u的父亲节点
dep[u]	保存结点u的深度值
size[u]	保存以u为根的子树节点个数
son[u]	保存重儿子
rk[u]	保存当前dfs标号在树中所对应的节点
top[u]	保存当前节点所在链的顶端节点
id[u]	保存树中每个节点剖分以后的新编号

　　　　   树链剖分是由两次dfs来实现的，第一次dfs处理出每个点的重儿子，子树大小，深度及父节点，第二遍dfs处理出每个点所在重链的链头。

　　　　 下面给出树链剖分实现求lca的程序。

 1 void dfs1(re int x,re int ff){
 2     fa[x]=ff,dep[x]=dep[ff]+1,siz[x]++;
 3     for(re int i=first[x];i;i=edge[i].next){
 4         re int y=edge[i].v;
 5         if(dep[y]||y==ff) continue;
 6         dfs1(y,x);siz[x]+=siz[y];
 7         if(siz[y]>siz[son[x]]) son[x]=y;
 8     }
 9 }
10 void dfs2(re int x,re int pt){
11     top[x]=pt;
12     if(son[x]) dfs2(son[x],pt);
13     for(re int i=first[x];i;i=edge[i].next){
14         re int y=edge[i].v;
15         if(y==son[x]||y==fa[x]) continue;
16         dfs2(y,y);
17     }
18 }
19 inline int lca(re int x,re int y){
20     while(top[x]!=top[y]){
21         if(dep[top[x]]<dep[top[y]]) x^=y^=x^=y;
22         x=fa[top[x]];
23     }
24     return dep[x]<dep[y]?x:y;
25 }

树链剖分求lca