拓扑排序的简单证明以及由来

Posted 2021-03-18 rotepad

介绍

拓扑排序，很多人都可能听说但是不了解的一种算法。或许很多人只知道它是图论的一种排序，至于干什么的不清楚。又或许很多人可能还会认为它是一种啥排序。而实质上它是对有向图的顶点排成一个线性序列。

至于定义，百科上是这么说的：

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

为什么会有拓扑排序？拓扑排序有何作用？

举个例子，学习java系列的教程
代号 | 科目| 学前需掌握|
-------- | ----- | --|
A1 | javaSE|
A2 | html|
A3 | Jsp|A1，A2
A4 | servlet|A1
A5 | ssm|A3,A4
A6 | springboot|A5
就比如学习java系类(部分)从java基础，到jsp/servlet，到ssm，到springboot，springcloud等是个循序渐进且有依赖的过程。在jsp学习要首先掌握java基础和html基础。学习框架要掌握jsp/servlet和jdbc之类才行。那么，这个学习过程即构成一个拓扑序列。当然这个序列也不唯一，你可以对不关联的学科随意选择顺序(比如html和java可以随便先开始哪一个。)

那上述序列可以简单表示为：

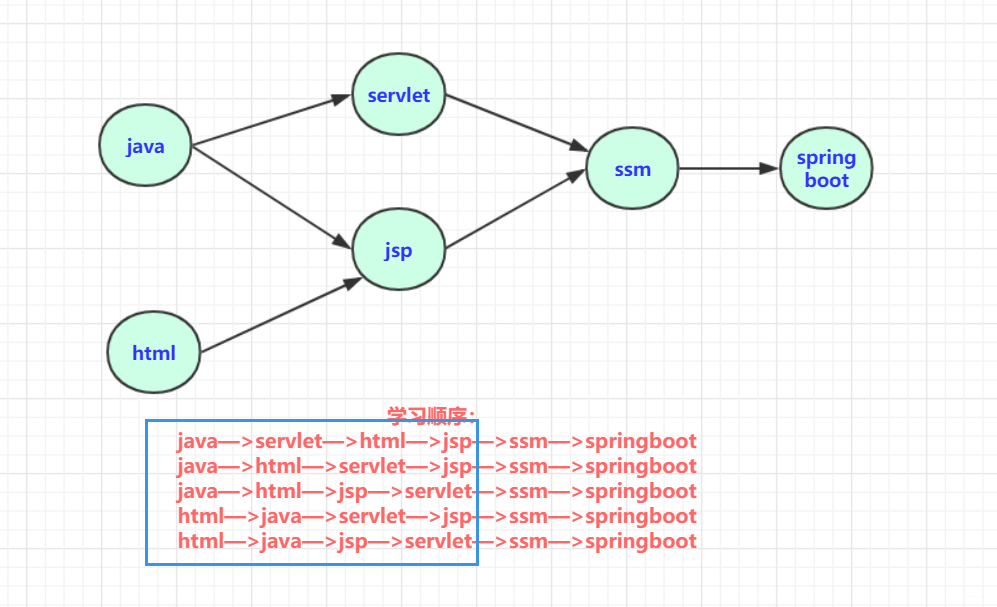
其中五种均为可以选择的学习方案，对课程安排可以有参考作用，当然，五个都是拓扑序列。只是选择的策略不同！

一些其他注意：

DGA：有向无环图
AOV网：数据在顶点 可以理解为面向对象
AOE网：数据在边上，可以理解为面向过程！

而我们通俗一点的说法，就是按照某种规则将这个图的顶点取出来，这些顶点能够表示什么或者有什么联系。

规则：

• 图中每个顶点只出现一次。
• A在B前面，则不存在B在A前面的路径。(不能成环！！！！)
• 顶点的顺序是保证所有指向它的下个节点在被指节点前面！(例如A—>B—>C那么A一定在B前面，B一定在C前面)。所以，这个核心规则下只要满足即可，所以拓扑排序序列不一定唯一！

拓扑排序算法分析

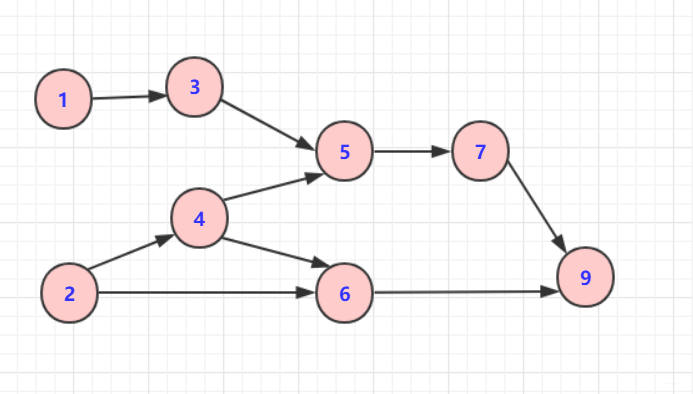
正常步骤为(方法不一定唯一)：

• 从DGA图中找到一个没有前驱的顶点输出。(可以遍历，也可以用优先队列维护)
• 删除以这个点为起点的边。(它的指向的边删除，为了找到下个没有前驱的顶点)
• 重复上述，直到最后一个顶点被输出。如果还有顶点未被输出，则说明有环！

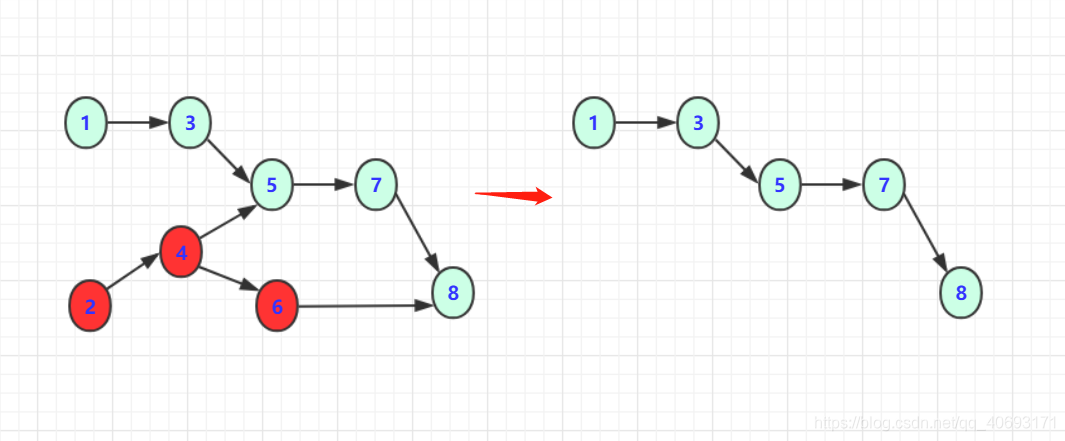
对于上图的简单序列，可以简单描述步骤为：

• 1：删除1或2输出
  
• 2：删除2或3以及对应边
  
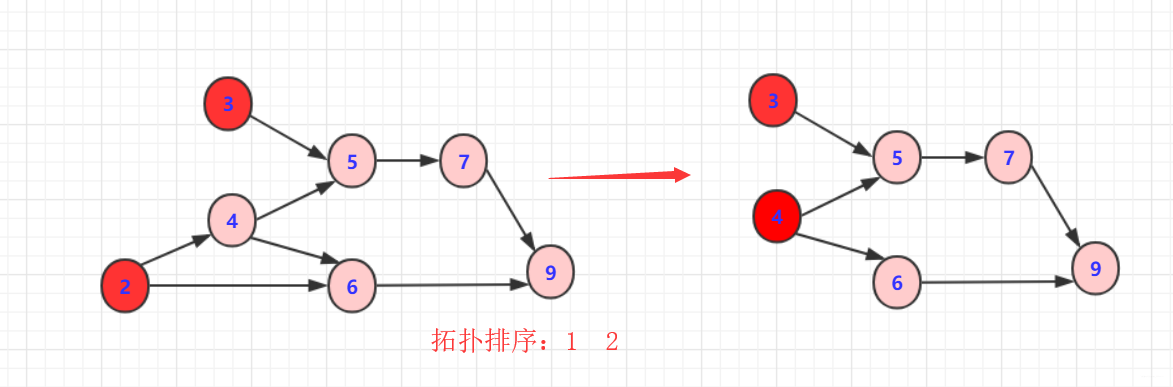
• 3：删除3或者4以及对应边
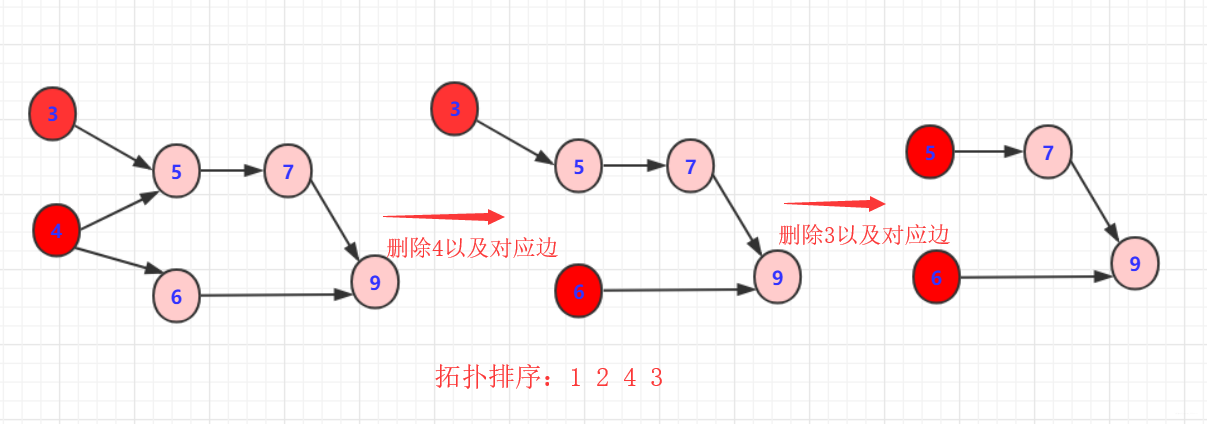
• 3：重复以上规则步骤
  

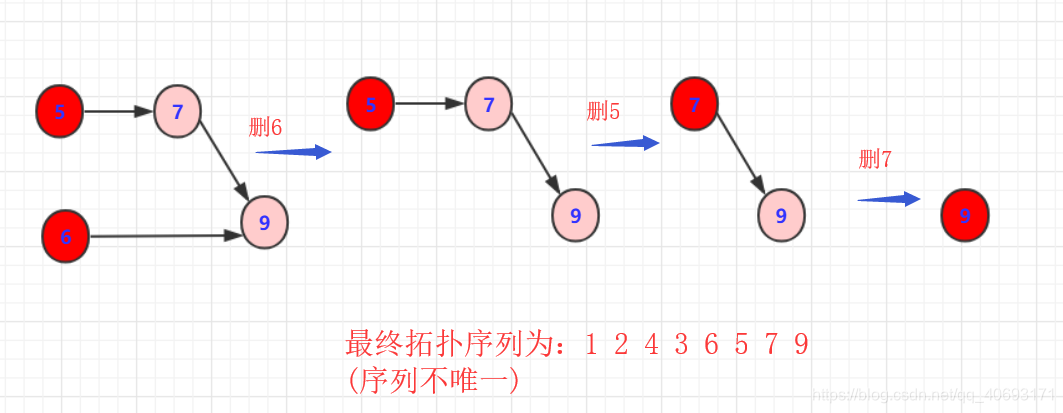
这样就完成一次拓扑排序，得到一个拓扑序列，但是这个序列并不唯一！从过程中也看到有很多选择方案，具体得到结果看你算法的设计了。但只要满足即是拓扑排序序列。

另外观察 1 2 4 3 6 5 7 9这个序列满足我们所说的有关系的节点指向的在前面，被指向的在后面。如果完全没关系那不一定前后(例如1,2)

拓扑排序代码实现

对于拓扑排序，如何用代码实现呢？对于拓扑排序，虽然在上面详细介绍了思路和流程，也很通俗易懂。但是实际上代码的实现还是很需要斟酌的，如何在空间和时间上能够得到较好的平衡且取得较好的效率？

首先要考虑存储。对于节点，首先他有联通点这么多属性。遇到稀疏矩阵还是用邻接表比较好。因为一个节点的指向节点较少，用邻接矩阵较浪费资源。

另外，如果是1，2，3，4，5，6这样的序列求拓扑排序，我们可以考虑用数组，但是如果遇到1，2，88，9999类似数据，可以考虑用map中转一下。那么，

我们具体的代码思想为：

• 新建node类，包含节点数值和它的指向(这里直接用list集合替代链表了)
• 一个数组包含node(这里默认编号较集中)。初始化，添加每个节点指向的时候同时被指的节点入度+1！(A—>C)那么C的入度+1；
• 扫描一遍所有node。将所有入度为0的点加入一个栈(队列)。
• 当栈(队列)不空的时候，抛出其中任意一个node(栈就是尾，队就是头，顺序无所谓，上面分析了只要同时入度为零可以随便选择顺序)。将node输出，并且node指向的所有元素入度减一。如果某个点的入度被减为0，那么就将它加入栈(队列)。
• 重复上述操作，直到栈为空。

这里主要是利用栈或者队列储存入度只为0的节点，只需要初次扫描表将入度为0的放入栈(队列)中。

Bb一1①：

A.notorious B.strand C.check in D.deposit E.surplus F.donation G.tenant H.guarantee I.verify J.deal K.procure L.heading M.tender N.proposal O.estimate P.subcontractor Q.infrastructure R.enterprise S.domestic T.expeditious

1~5.GPAHD
6~10.RIFBM
11~15.NLETJ
16~20.KCSQO

1~5.TTFTT
6~8.FFF

1~5.TFTTT
6~8.FFF

1.on a large scale
2.senior
3.Sort out
4.worksites
5.reception
6.profile
7.supervision
8.external
9.purposes

1.deliberate
2.significance
3.delivered
4.on the spot
5.monthly
6.entitled
7.accessible
8.Confirm
9.Schedule
10.simultaneously
翻译：
A1: The customer wants to open a letter of credit (L/C) for his company.

A2:There is not RMB ￥4,000,000 on their account.

A3:He can offer some mortgage.

A4: Because even one small mistake will bring him a great loss.

A5:No, he doesn’t.

 

• 这里你或许会问为什么。
• 因为节点之间是有相关性的，一个节点若想入度为零，那么它的父节点(指向节点)肯定在它为0前入度为0，拆除关联箭头。从父节点角度，它的这次拆除联系，可能导致被指向的入读为0，也可能不为0(还有其他节点指向儿子)
• 一个较大的工程往往被划分成许多子工程，我们把这些子工程称作活动(activity)。在整个工程中，有些子工程(活动)必须在其它有关子工程完成之后才能开始，也就是说，一个子工程的开始是以它的所有前序子工程的结束为先决条件的，但有些子工程没有先决条件，可以安排在任何时间开始。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系，可用一个有向图来表示，图中的顶点代表活动(子工程)，图中的有向边代表活动的先后关系，即有向边的起点的活动是终点活动的前序活动，只有当起点活动完成之后，其终点活动才能进行。通常，我们把这种顶点表示活动、边表示活动间先后关的有向图称做顶点活动网(Activity On Vertex network)，简称AOV网。

  • 对于二进制我相信大部分读者刚开始接触一定是一脸蒙蔽，当初我也是，但是通过长时间的刷题，二进制各种各样的操作都有了一些接触，我通过将每次刷题中有关于二进制的操作全都总结起来，今天在学树状数组时发现总结的还是有一点了，于是打算分享一下，毕竟这个神奇的二进制还是挺让人头疼的。

    以下附上我的总结（其实也是从各种博客，百度百科，360问答中弃其糟粕取其精华，总结的）：

    C/C++我知道的部分常用的位运算主要如下几个：

    a<<1左移运算，二进制的11(十进制为3)，操作后为110（十进制为6），相当于十进制乘2

    a<<2相当于十进制乘以4

 

Bb八⑧：

A. aisle B.layover C. plead D.overdraft E.banknote F. calamity G. tenant H. guarantee I. deal J. real estate agent K. exceed L. vendor M. supervise N. surefire O. formula P. quote Q. rectification R. helmet S. infrastructure T. domestic

1~5.NSFKD
6~10.TLMPB
11~15.QHOIJ
16~20.RCGEA

1~5.FFTFT
6~8.TFF

1~5.TFTTT
6~8.FFF

administers
citizens
confusion
stamp
baggage
facilitates
inspect
restricted
guidelines

available
invented
experience
convenient
amount
cash
earned
invest
investment
valuable

A1: Regional manager of overseas office of North China Electric Power Company.

A2: Every proposal will be kept by specially assigned person.

A3: He wanted to know something about submission of bid for No. 1 power plant.

A4: From 5th May to 15th May.

A5: Because his company will have an important meeting in Shanghai and all members except a junior clerk in overseas office will attend.

 

x=1<<k;    x等于2的k次方 （树状数组中可以运用到）

-i 表示将二进制反转，1变成0，0变成1，最后再在末尾加上1（若最后一位为1就满2进1）----可运用于树状数组lowbit运算

 

x<<1等于x*2（线段树可以运用到）

x<<1|1等于x*2+1（线段树中可以运用）

a>>1右移运算，二进制的111和110，操作后都为11，相当于除2

>> 右移运算相当于整数除法10>>2 = 10 / 4 = 

• 

  图3-5 这种先后关系的AOV网

  三3③：

  A.aisle B.portable C.layover D. overdraft E.current account F.banknote G.landlord H. celebrity I. budget J.debit K. specification L. exceed M. side effect N. addenda O. review P. assumption Q. indispensable R. foreman S. inspection T. stipulate
  1~5.CIJMD
  6~10.ANEPS
  11~15.BRHTG
  16~20.FLOQK

  
  1~5.TTFFT
  6~8.TFT

  1~5.FFTFT
  6~8.TFF

  administers
  citizens
  confusion
  stamp
  baggage
  facilitates
  inspect
  restricted
  guidelines

  available
  invented
  experience
  convenient
  amount
  cash
  earned
  invest
  investment
  valuable

  题目：
  A1: Assistant of Mr. Williams

  A2: Before next Friday.

  A3: Airfield runway and Terminal 1.

  A4: From 9th September to 19th September.

  A5: Because his company has another big program during the time set for the bidders to submit their bids.

  对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。
  拓扑排序对应施工的流程图具有特别重要的作用，它可以决定哪些子工程必须要先执行，哪些子工程要在某些工程执行后才可以执行。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系，可用一个有向图来表示，图中的顶点代表活动(子工程)，图中的有向边代表活动的先后关系，即有向边的起点的活动是终点活动的前序活动，只有当起点活动完成之后，其终点活动才能进行。通常，我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network)，简称AOV网。
  一个AOV网应该是一个有向无环图，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行（对于数据流来说就是死循环）。在AOV网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列(Topological order)，由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的，满足上述定义的任一线性序列都称作它的拓扑序列。

  2、拓扑排序的实现步骤
  在有向图中选一个没有前驱的顶点并且输出
  从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）
  重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。
  3、拓扑排序示例手动实现
  如果我们有如下的一个有向无环图，我们需要对这个图的顶点进行拓扑排序，过程如下：

  四4④：

  A.customs B.plead C.passport D.facilitate E.calamity F.durable G.tenancy H.torment I.housekeeping J.lease K.vendor L.submit M.supervise N.surefire O.devastate P.formula Q.kick off R.confidential S.facility T.countermeasure

  1~5.DIPAN
  6~10.JBCFL
  11~15.GREST
  16~20.HMQOK

  1~5.TTFTT
  6~8.FFF

  1~5.FFTFT
  6~8.TFF

  on a large scale
  senior
  Sort out
  worksites
  reception
  profile
  supervision
  external
  purposes
  
  available
  invented
  experience
  convenient
  amount
  cash
  earned
  invest
  investment
  valuable

  A1: Prequalification document.

  A2: The name of the bidder’s head office.

  A3: Head office’s address first and overseas office’s address in the column of Remarks.

  A4: He had to list all the legal cases your company may have been involved in past 3 years, if any.

  A5: A certificate from an honorable bank indicating the bidder’s credit record.

  
  首先，我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果：

  
  然后，我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果：

  
  然后，我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果：

  
  然后，我们输出没有前驱的顶点V3，得到如下结果：

  
  然后，我们分别输出V5和V2，最后全部顶点输出完成，该图的一个拓扑序列为：

  v6–>v1—->v4—>v3—>v5—>v2

  4、拓扑排序的代码实现
  下面，我们将用两种方法来实现我么的拓扑排序：

  六6⑥：

  A. carousel B. notorious C. terminal D. endorse E. balance F. interest rate G. flatmate H. verify I. budget J. haggle K. evaluate L. identify M. procure N. confidentiality O. proposal P. eliminate Q. infrastructure R. domestic S. panic T. knack

  1~5.NPTLB
  6~10.KEFQJ
  11~15.MHORD
  16~20.SCIGA

  1~5.TFTTT
  6~8.FFF

  1~5.TFTFF
  6~8.TTT

  
  administers
  citizens
  confusion
  stamp
  baggage
  facilitates
  inspect
  restricted
  guidelines

  recommended
  total
  accompanied
  sealed
  closing
  rejected
  warranty
  non-refundable
  returned
  awarded

  A1: To get his check-books.

  A2: The first part is the check number, the middle part is our bank code number, while the last part is the account number.

  A3: At the bottom of the check.

  A4: Draw a line from the end of the amount to the word dollars.

  A5: It means signing the name of the payer on the back of the check.

  Kahn算法
  基于DFS的拓扑排序算法
  首先我们先介绍第一个算法的思路：
  Kahn的算法的思路其实就是我们之前那个手动展示的拓扑排序的实现，我们先使用一个栈保存入度为0 的顶点，然后输出栈顶元素并且将和栈顶元素有关的边删除，减少和栈顶元素有关的顶点的入度数量并且把入度减少到0的顶点也入栈。具体的代码如下：

  七7⑦：

  A.strand B.check in C.sprint D.deposit E.donation F.custody G.tenancy H.real estate agent I.torment J.lease K.heading L.tender M.contractor N.estimate O.award P.clarification Q.indispensable R.inspection S.kick off T.facility
  Question

  1~5.MSTCN
  6~8.KDOFI
  11~15.LHRJQ
  16~20.PBEGA

  1~5.TTFTT
  6~8.FFF

  1~5.TTFFT
  6~8.TFT

  on a large scale
  senior
  Sort out
  worksites
  reception
  profile
  supervision
  external
  purposes
  
  deliberate
  significance
  delivered
  on the spot
  monthly
  entitled
  accessible
  Confirm
  Schedule
  simultaneously

  A1: A power engineering construction project in Freetown.

  A2: The advanced electric generator.

  A3: From 15th October to 30th October.

  A4: A cash deposit or a letter of guarantee from a commercial bank.

  A5: The cash deposit or the letter of guarantee shall be returned to the bidder within one week after the decision on award is declared.

  例如，假定一个计算机专业的学生必须完成图3-4所列出的全部课程。在这里，课程代表活动，学习一门课程就表示进行一项活动，学习每门课程的先决条件是学完它的全部先修课程。如学习《数据结构》课程就必须安排在学完它的两门先修课程《离散数学》和《算法语言》之后。学习《高等数学》课程则可以随时安排，因为它是基础课程，没有先修课。若用AOV网来表示这种课程安排的先后关系，则如图3-5所示。图中的每个顶点代表一门课程，每条有向边代表起点对应的课程是终点对应课程的先修课。从图中可以清楚地看出各课程之间的先修和后续的关系。如课程C5的先修课为C2，后续课程为C4和C6。 [2] 
  一个AOV网应该是一个有向无环图，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行。如图3-6是一个具有三个顶点的回路，由<A,B>边可得B活动必须在A活动之后，由<B,C>边可得C活动必须在B活动之后，所以推出C活动必然在A活动之后，但由<C,A>边可得C活动必须在A活动之前，从而出现矛盾，使每一项活动都无法进行。这种情况若在程序中出现，则称为死锁或死循环，是应该必须避免的。
  在AOV网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列(Topological order)，由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的，满足上述定义的任一线性序列都称作它的拓扑序列。
  由AOV网构造出拓扑序列的实际意义是：如果按照拓扑序列中的顶点次序，在开始每一项活动时，能够保证它的所有前驱活动都已完成，从而使整个工程顺序进行，不会出现冲突的情况。 [2] 

至于具体demo：

package 图论;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;

public class tuopu {
    static class node
    {
        int value;
        List<Integer> next;
        public node(int value) {
            this.value=value;
            next=new ArrayList<Integer>();
        }
        public void setnext(List<Integer>list) {
            this.next=list;
        }
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        node []nodes=new node[9];//储存节点
        int a[]=new int[9];//储存入度
        List<Integer>list[]=new ArrayList[10];//临时空间，为了存储指向的集合
        for(int i=1;i<9;i++)
        {
            nodes[i]=new node(i);
            list[i]=new ArrayList<Integer>();
        }
        initmap(nodes,list,a);
        
        //主要流程
        //Queue<node>q1=new ArrayDeque<node>();
        Stack<node>s1=new Stack<node>();
        for(int i=1;i<9;i++)
        {
            //System.out.print(nodes[i].next.size()+" 55 ");
            //System.out.println(a[i]);
            if(a[i]==0) {s1.add(nodes[i]);}
            
        }
        while(!s1.isEmpty())
        {
            node n1=s1.pop();//抛出输出
            
            System.out.print(n1.value+" ");
            
            List<Integer>next=n1.next;
            for(int i=0;i<next.size();i++)
            {
                a[next.get(i)]--;//入度减一
                if(a[next.get(i)]==0)//如果入度为0
                {
                    s1.add(nodes[next.get(i)]);
                }
            }
        }
    }

    private static void initmap(node[] nodes, List<Integer>[] list, int[] a) {
        list[1].add(3);
        nodes[1].setnext(list[1]);
        a[3]++;
        list[2].add(4);list[2].add(6);
        nodes[2].setnext(list[2]);
        a[4]++;a[6]++;
        list[3].add(5);
        nodes[3].setnext(list[3]);
        a[5]++;
        list[4].add(5);list[4].add(6);
        nodes[4].setnext(list[4]);
        a[5]++;a[6]++;
        list[5].add(7);
        nodes[5].setnext(list[5]);
        a[7]++;
        list[6].add(8);
        nodes[6].setnext(list[6]);
        a[8]++;
        list[7].add(8);
        nodes[7].setnext(list[7]);
        a[8]++;
        
    }
}

输出结果

2 4 6 1 3 5 7 8

当然，上面说过用栈和队列都可以！如果使用队列就会得到1 2 3 4 5 6 7 8的拓扑序列

至于图的构造，因为没有条件可能效率并不高，算法也可能不太完美，如有优化错误还请大佬指正！