数据结构课设——有向图的深度广度优先遍历及拓扑排序

Posted 2021-03-13 nqqqy

任务：给定一个有向图，实现图的深度优先, 广度优先遍历算法，拓扑有序序列，并输出相关结果。

功能要求：输入图的基本信息，并建立图存储结构（有相应提示），输出遍历序列，然后进行拓扑排序，并测试该图是否为有向无环图，并输出拓扑序列。

按照惯例，先上代码，注释超详细：

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#pragma warning(disable:4996)
#define Max 20//定义数组元素最大个数（顶点最大个数）
typedef struct node//边表结点
{
    int adjvex;//该边所指向结点对应的下标
    struct node* next;//该边所指向下一个结点的指针
}eNode;
typedef struct headnode//顶点表结点
{
    int in;//顶点入度
    char vertex;//顶点数据
    eNode* firstedge;//指向第一条边的指针，边表头指针
}hNode;
typedef struct//邻接表（图）
{
    hNode adjlist[Max];//以数组的形式存储
    int n, e;//顶点数，边数
}linkG;

//以邻接表的存储结构创建图
linkG* creat(linkG* g)
{
    int i, k;
    eNode* s;//边表结点
    int n1, e1;
    char ch;
    g = (linkG*)malloc(sizeof(linkG));//申请结点空间
    printf("请输入顶点数和边数：");
    scanf("%d%d", &n1, &e1);
    g->n = n1;
    g->e = e1;
    printf("顶点数：%d    边数：%d
", g->n, g->e);
    printf("请输入顶点信息（字母）：");
    getchar();//因为接下来要输入字符串，所以getchar用于承接上一条命令的结束符
    for (i = 0; i < n1; i++)
    {
        scanf("%c", &ch);
        g->adjlist[i].vertex = ch;//获得该顶点数据
        g->adjlist[i].firstedge = NULL;//第一条边设为空
    }
    printf("
打印顶点下标及顶点数据：
");
    for (i = 0; i < g->n; i++)//循环打印顶点下标及顶点数据
    {
        printf("顶点下标：%d  顶点数据：%c
", i, g->adjlist[i].vertex);
    }
    getchar();
    int i1, j1;//相连接的两个顶点序号
    for (k = 0; k < e1; k++)//建立边表
    {

        printf("请输入对<i,j>（空格分隔）：");
        scanf("%d%d", &i1, &j1);
        s = (eNode*)malloc(sizeof(eNode));//申请边结点空间
        s->adjvex = j1;//边所指向结点的位置，下标为j1
        s->next = g->adjlist[i1].firstedge;//将当前s的指针指向当前顶点上指向的结点
        g->adjlist[i1].firstedge = s;//将当前顶点的指针指向s
    }
    return g;//返回指针g
}
int visited[Max];//标记是否访问
void DFS(linkG* g, int i)//深度优先遍历
{
    eNode* p;
    printf("%c ", g->adjlist[i].vertex);
    visited[i] = 1;//将已访问过的顶点visited值改为1
    p = g->adjlist[i].firstedge;//p指向顶点i的第一条边
    while (p)//p不为NULL时（边存在）
    {
        if (visited[p->adjvex] != 1)//如果没有被访问
        {
            DFS(g, p->adjvex);//递归
        }
        p = p->next;//p指向下一个结点
    }
}
void DFSTravel(linkG* g)//遍历非连通图
{
    int i;
    printf("深度优先遍历;
");
    //printf("%d
",g->n);
    for (i = 0; i < g->n; i++)//初始化为0
    {
        visited[i] = 0;
    }
    for (i = 0; i < g->n; i++)//对每个顶点做循环
    {
        if (!visited[i])//如果没有被访问
        {
            DFS(g, i);//调用DFS函数
        }
    }
}
void BFS(linkG* g, int i)//广度优先遍历
{
    int j;
    eNode* p;
    int q[Max], front = 0, rear = 0;//建立顺序队列用来存储，并初始化
    printf("%c ", g->adjlist[i].vertex);
    visited[i] = 1;//将已经访问过的改成1
    rear = (rear + 1) % Max;//普通顺序队列的话，这里是rear++
    q[rear] = i;//当前顶点（下标）队尾进队
    while (front != rear)//队列非空
    {
        front = (front + 1) % Max;//循环队列，顶点出队
        j = q[front];
        p = g->adjlist[j].firstedge;//p指向出队顶点j的第一条边
        while (p != NULL)
        {
            if (visited[p->adjvex] == 0)//如果未被访问
            {
                printf("%c ", g->adjlist[p->adjvex].vertex);
                visited[p->adjvex] = 1;//将该顶点标记数组值改为1
                rear = (rear + 1) % Max;//循环队列
                q[rear] = p->adjvex;//该顶点进队
            }
            p = p->next;//指向下一个结点
        }
    }
}
void BFSTravel(linkG* g)//遍历非连通图
{
    int i;
    printf("广度优先遍历：
");
    for (i = 0; i < g->n; i++)//初始化为0
    {
        visited[i] = 0;
    }
    for (i = 0; i < g->n; i++)//对每个顶点做循环
    {
        if (!visited[i])//如果没有被访问过
        {
            BFS(g, i);//调用BFS函数
        }
    }
}
//因为拓扑排序要求入度为0，所以需要先求出每个顶点的入度
void inDegree(linkG* g)//求图顶点入度
{
    eNode* p;
    int i;
    for (i = 0; i < g->n; i++)//循环将顶点入度初始化为0
    {
        g->adjlist[i].in = 0;
    }
    for (i = 0; i < g->n; i++)//循环每个顶点
    {
        p = g->adjlist[i].firstedge;//获取第i个链表第1个边结点指针
        while (p != NULL)///当p不为空（边存在）
        {
            g->adjlist[p->adjvex].in++;//该边终点结点入度+1
            p = p->next;//p指向下一个边结点
        }
        printf("顶点%c的入度为：%d
", g->adjlist[i].vertex, g->adjlist[i].in);
    }

}
void topo_sort(linkG *g)//拓扑排序
{
    eNode* p;
    int i, k, gettop;
    int top = 0;//用于栈指针的下标索引
    int count = 0;//用于统计输出顶点的个数
    int* stack=(int *)malloc(g->n*sizeof(int));//用于存储入度为0的顶点
    for (i=0;i<g->n;i++)//第一次搜索入度为0的顶点
    {
        if (g->adjlist[i].in==0)
        {
            stack[++top] = i;//将入度为0的顶点进栈
        }
    }
    while (top!=0)//当栈不为空时
    {
        gettop = stack[top--];//出栈,并保存栈顶元素（下标）
        printf("%c ",g->adjlist[gettop].vertex);
        count++;//统计顶点
        //接下来是将邻接点的入度减一，并判断该点入度是否为0
        p = g->adjlist[gettop].firstedge;//p指向该顶点的第一条边的指针
        while (p)//当p不为空时
        {
            k = p->adjvex;//相连接的顶点（下标）
            g->adjlist[k].in--;//该顶点入度减一
            if (g->adjlist[k].in==0)
            {
                stack[++top] = k;//如果入度为0，则进栈
            }
            p = p->next;//指向下一条边
        }
    }
    if (count<g->n)//如果输出的顶点数少于总顶点数，则表示有环
    {
        printf("
有回路！
");
    }
    free(stack);//释放空间
}
void menu()//菜单
{
    system("cls");//清屏函数
    printf("************************************************
");
    printf("*             1.建立图                         *
");
    printf("*             2.深度优先遍历                   *
");
    printf("*             3.广度优先遍历                   *
");
    printf("*             4.求出顶点入度                   *
");
    printf("*             5.拓扑排序                       *
");
    printf("*             6.退出                           *
");
    printf("************************************************
");
}
int main()
{
    linkG* g = NULL;
    int c;
    while (1)
    {
        menu();
        printf("请选择：");
        scanf("%d", &c);
        switch (c)
        {
        case 1:g = creat(g); system("pause");
            break;
        case 2:DFSTravel(g); system("pause");
            break;
        case 3:BFSTravel(g); system("pause");
            break;
        case 4:inDegree(g); system("pause");
            break;
        case 5:topo_sort(g); system("pause");
            break;
        case 6:exit(0);
            break;
        }
    }
    return 0;
}

实验用图:

 

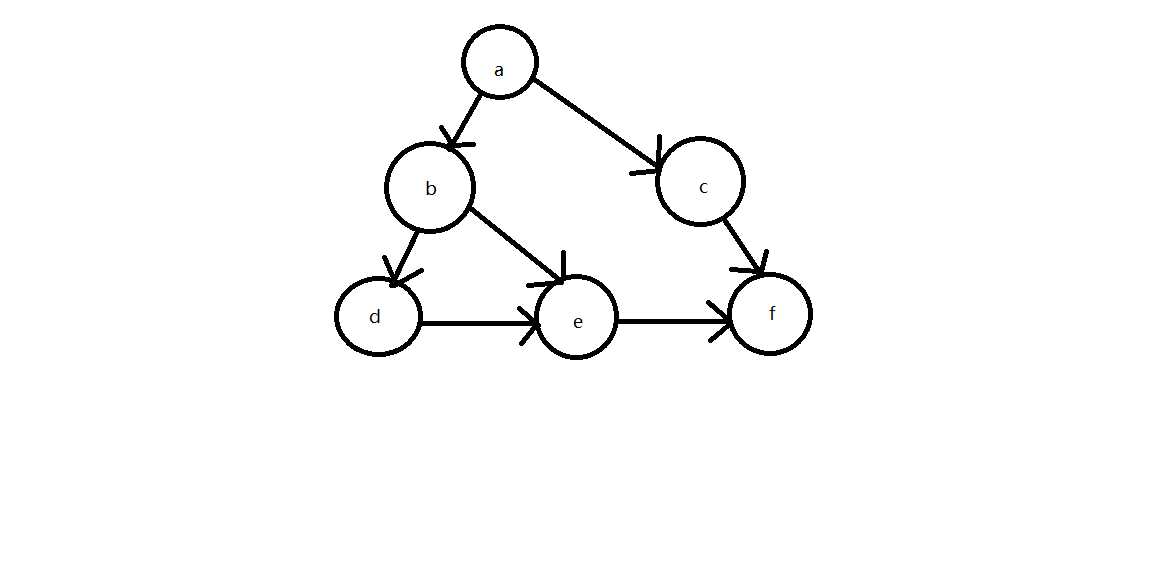
运行结果：

 

 

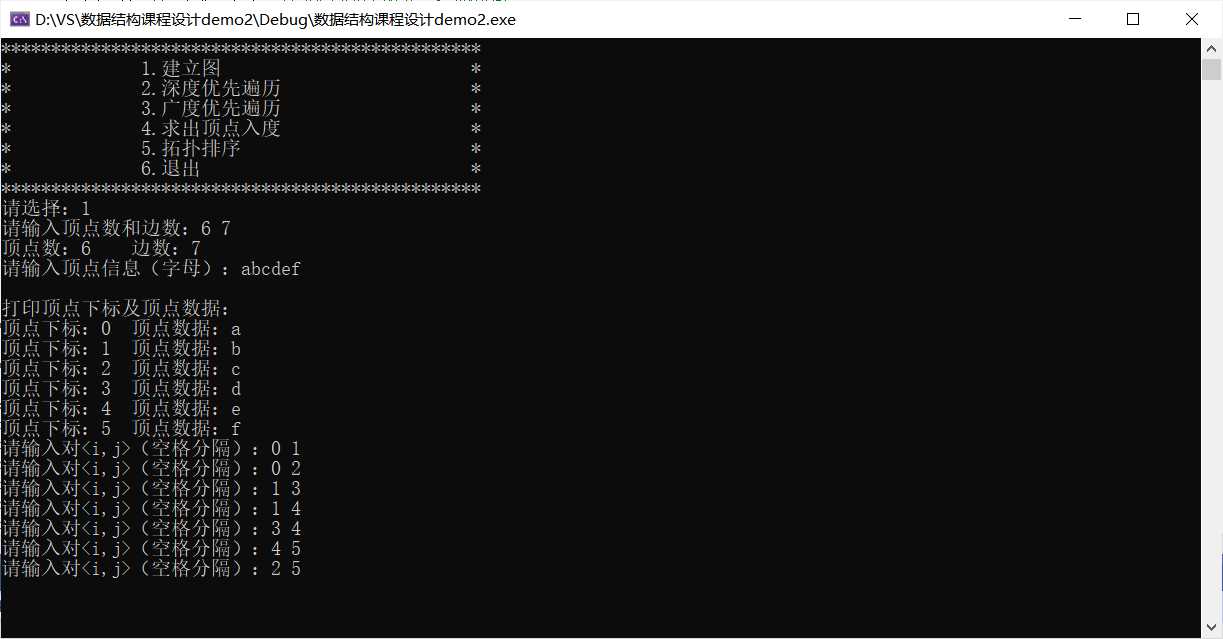
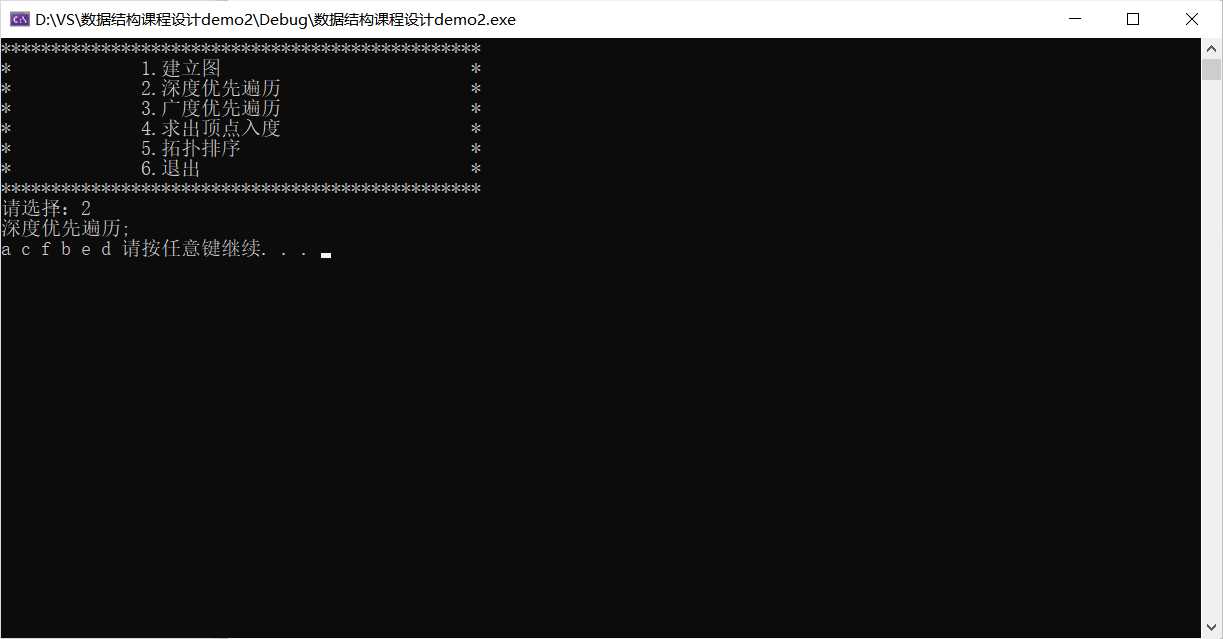
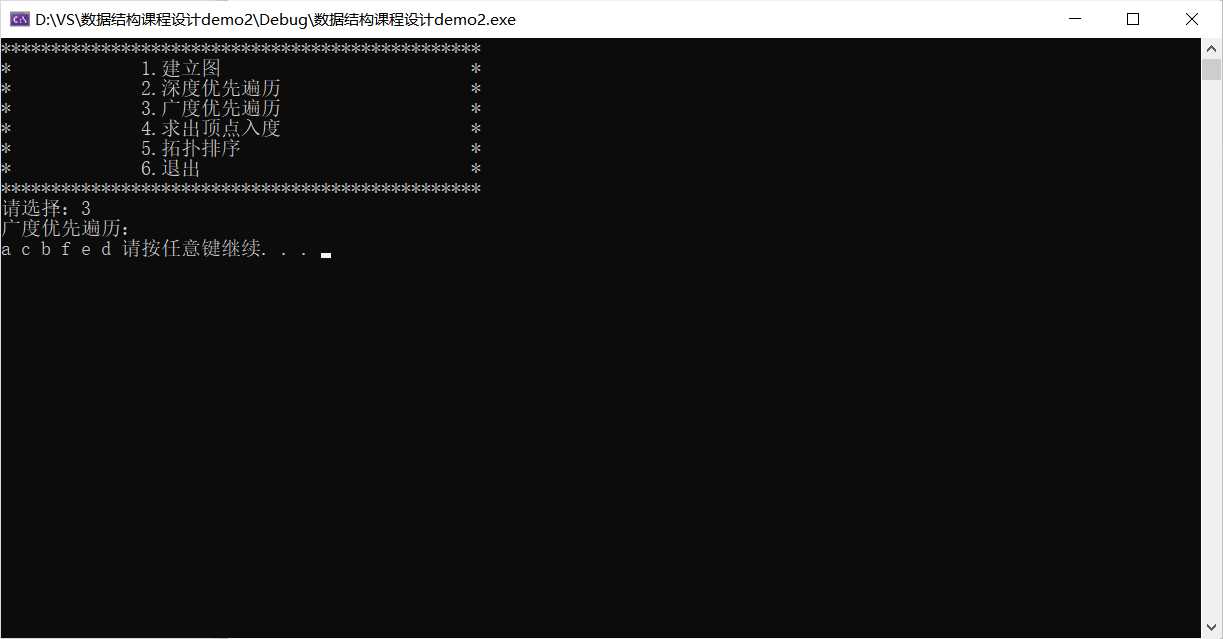
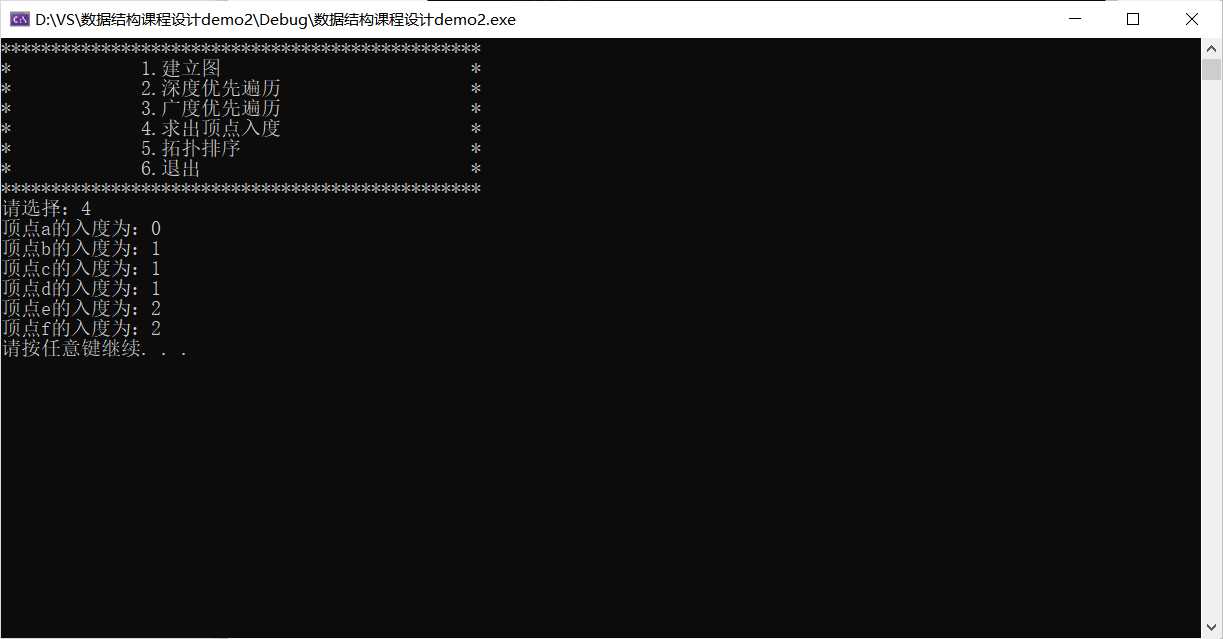
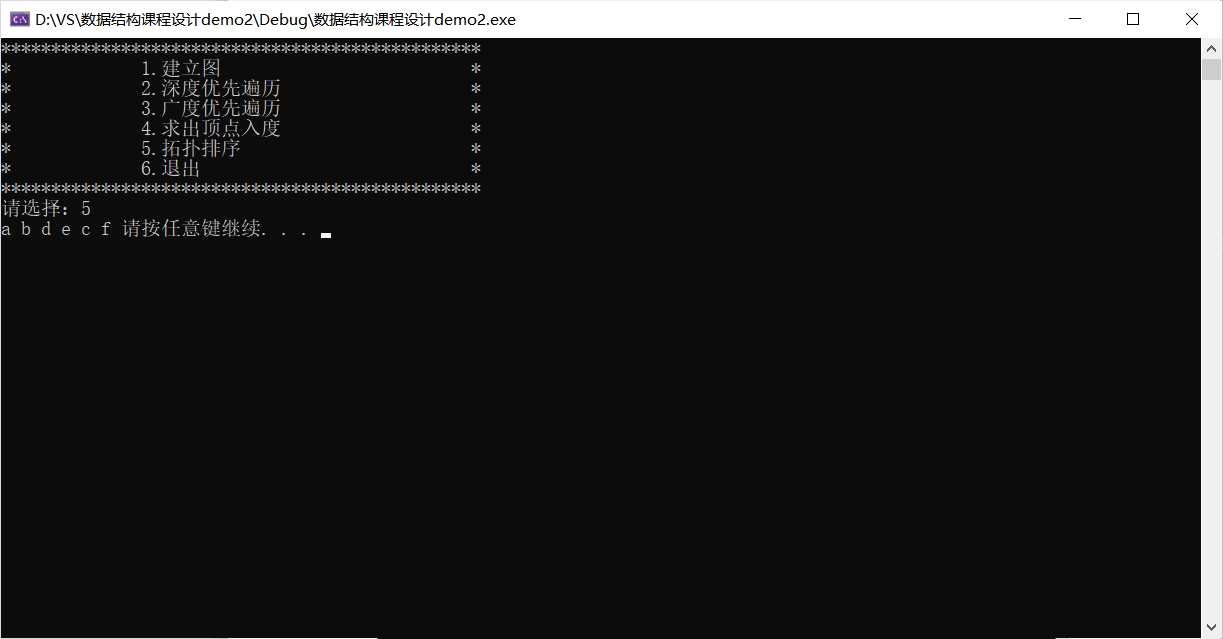
关于深度优先遍历

　　a.从图中某个顶点v出发，访问v。

　　b.找到刚访问过得顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问的顶点没有未被访问的邻接点为止。

　　c.返回前一个访问过得且扔有未被访问的邻接点的顶点，找到该顶点的下一个未被访问的邻接点，访问该顶点。

　　d.重复步骤2，3，直至图中所有顶点都被访问过。

时间复杂性:采用邻接表存储方法，它的e条边所对应的边结点的总个数为2e，调用DFS的时间为O(e)。此时算法的时间复杂度为O(n+e).当n<=e时，若不计置visited的时间，则整个深度优先搜索所需要的时间为O(e)。

 

关于广度优先遍历

首先访问指定出发顶点，然后依次访问该顶点的所有未被访问过的顶点，再接下来访问邻接点的未被访问过的邻接点，以此类推。由此可见，实现这个过程需要设置一个队列结构。

广度优先搜索是按层来处理顶点，距离开始点最近的那些顶点首先被访问，而最远的那些顶点则最后被访问，这个和树的层序变量很像，BFS的代码使用了一个队列。搜索步骤： 
  a .首先选择一个顶点作为起始顶点，并将其visited设为0 
  b. 将起始顶点放入队列中。 
  c. 从队列首部选出一个顶点，并找出所有与之邻接的顶点，将找到的邻接顶点放入队列尾部，将已访问过顶点visited设置为1，没访问过的顶点是0。
  d. 按照同样的方法处理队列中的下一个顶点。

时间复杂性：从算法中可知，每个顶点最多进队一次，n个顶点一共有n次进队操作，由于遍历的过程实际上是通过边或弧寻找邻接点的过程，因此广度优先搜索算法的时间复杂度与深度优先搜索算法地时间复杂度相同，两者空间复杂度均为O（n）。

 

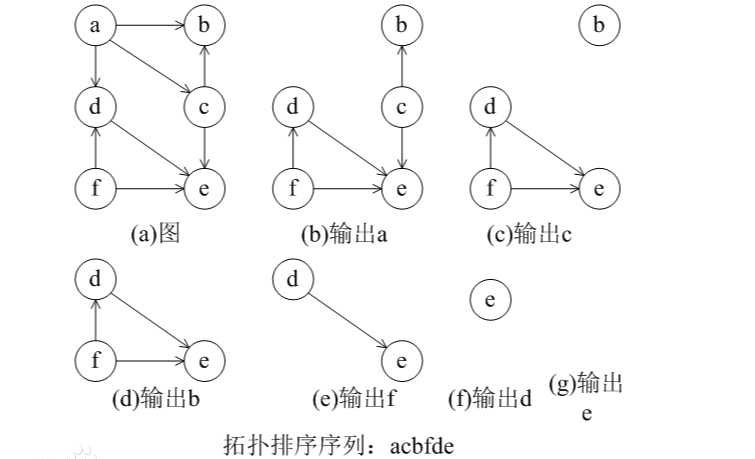
关于拓扑排序

在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。

先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。

一直做改操作，直到所有的节点都被分离出来。

如果最后不存在入度为0的节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。

时间复杂性：如果AOV网络有n个顶点，e条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是O(n)。在正常情况下，每个顶点进一次栈，出一次栈，所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。