一文通数据结构与算法之——图+常见题型与解题策略+Leetcode经典题

Posted 尚墨1111

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一文通数据结构与算法之——图+常见题型与解题策略+Leetcode经典题相关的知识，希望对你有一定的参考价值。

文章目录

数据结构——图

1 基本概念

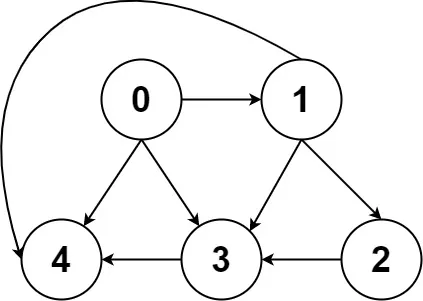
图：有向图、无向图、双向图

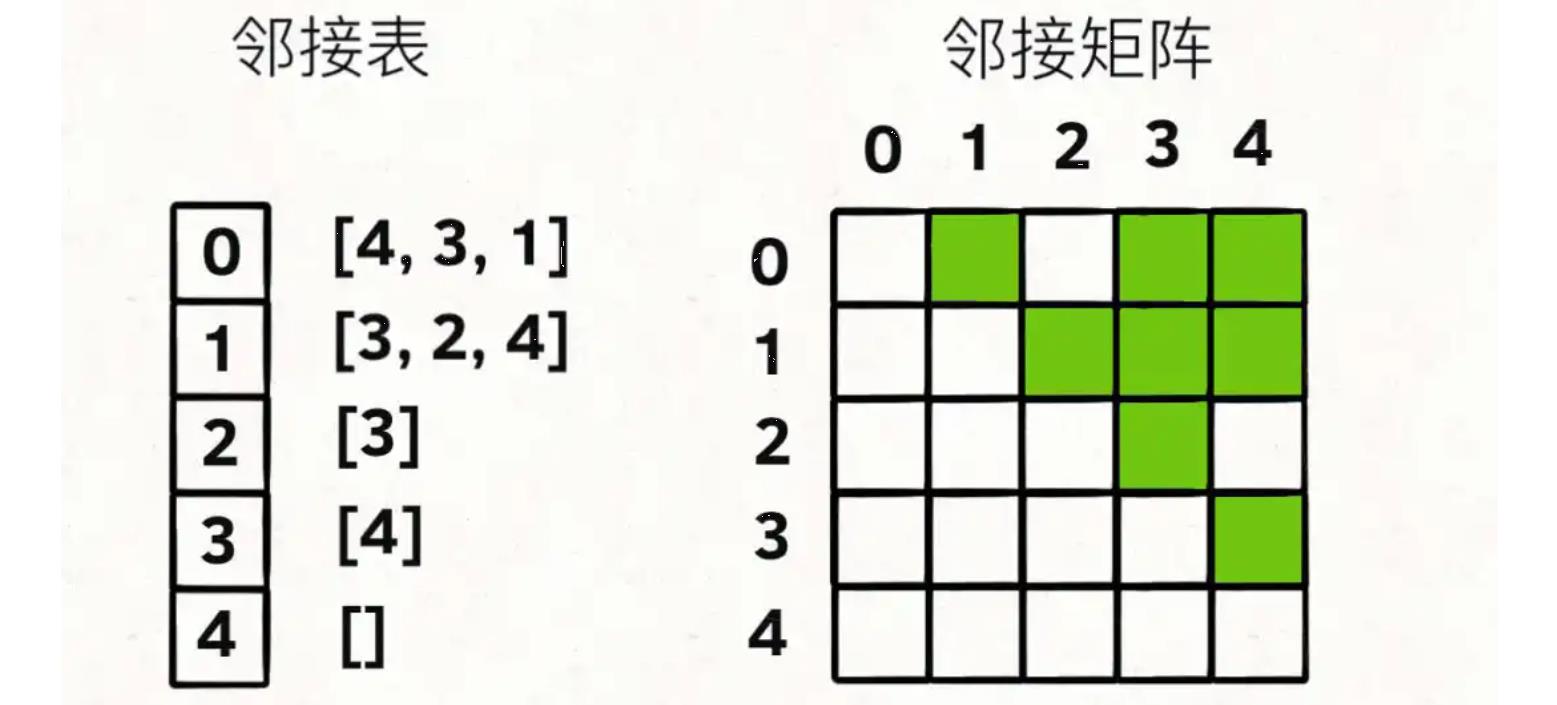
1.1 图的存储方式

  • 邻接表，我把每个节点x的邻居都存到一个列表里，然后把x和这个列表关联起来，可以通过一个节点x找到它的所有相邻节点。邻接表的主要优势是节约存储空间
List<Integer>[] graph;
// graph[s]是一个列表，存储着节点s所指向的节点。
  • 邻接矩阵，二维数组，我们权且成为matrix，如果节点x和y是相连的，那么就把matrix[x][y]设为true或者权重。如果想找节点x的邻居，去扫一圈matrix[x][..]就行了。邻接矩阵的主要优势是可以迅速判断两个节点是否相邻
int[][] matrix

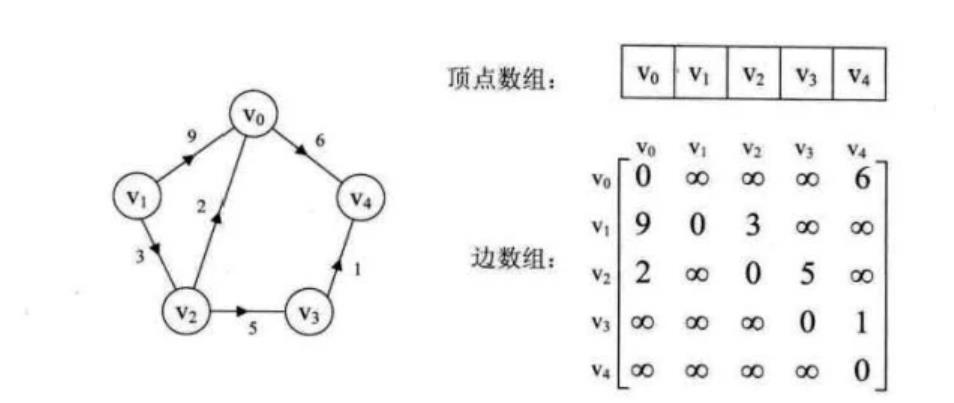
1.2 有向加权图

如果是邻接表，我们不仅仅存储某个节点x的所有邻居节点，还存储x到每个邻居的权重

如果是邻接矩阵，matrix[x][y]不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重

连接无向图中的节点x和y，把matrix[x][y]和matrix[y][x]都变成true不就行了；邻接表也是类似的操作

1.3 实现

图的节点类

/* 图节点的逻辑结构 */
class Vertex {
    int id;
    int[] neighbors;
}

和多叉树节点几乎完全一样：

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

1.4 图的遍历

图的遍历同二叉树的遍历，有两种方式：BFS、DFS，BFS递归回溯，DFS需要用到额外的对来来维持访问的顺序，类似按层遍历的思想

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;

    for (TreeNode child : root.children)
        traverse(child);
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。

所以，如果图包含环，遍历框架就要一个visited数组进行辅助：

Graph graph;
boolean[] visited;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s
    visited[s] = true;
    for (TreeNode neighbor : graph.neighbors(s))
        traverse(neighbor);
    // 离开节点 s
    visited[s] = false;   
}

1.4.1 深度优先遍历图 BFS

797. 所有可能的路径

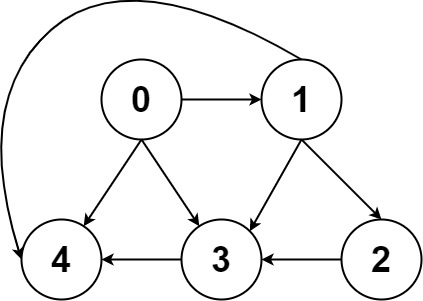
给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

// 记录所有路径
    List<List<Integer>> res = new LinkedList<>();

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph, 0, path);
        return res;
    }

    public void traverse(int[][] graph,int node,LinkedList<Integer> path){
//        1.选择节点
        path.add(node);
//        2.判断该节点是否是最后的节点
        int n = graph.length;
        if(node==n-1){
//            为什么创建新路径，直接用原来的不行吗？
            res.add(new LinkedList<>(path));
            path.removeLast();
            return;
        }
//        3.遍历当前节点所有与它相连的节点
        for (int vertex: graph[node]) {
            traverse(graph,vertex,path);
        }
//        4.遍历完毕，回退上一个选择
        path.removeLast();
    }

1.4.2 广度优先遍历图 BFS

分为有环和无环图的两种遍历

//模板
void bfs(){
    将起始点放入队列中
    标记起点访问//如果是有环图的话，需要另外维护一个访问数组，将访问过的节点进行标记
    while(如果队列不为空){
        访问队首元素
        删除队首元素
        for(x所有相邻的点){
            if(该点未被访问过且合法){
                将该点加入队列末尾
            }
        }
    }
     队列为空，广搜结束
}

   public List<List<Integer>> allPathsSourceTarget(int[][] graph) {        List<List<Integer>> ans  = new LinkedList<>();        int n = graph.length;        Queue<Node> queue = new LinkedList<>();        queue.add(new Node(0));        while(queue.size() > 0){            Node node = queue.poll();            if(node.index==n-1){                res.add(node.path);                continue;            }            for (int vertex : graph[node.index]) {                queue.offer(new Node(vertex,node.path));            }        }        return ans;    }class Node{    int index;    List<Integer> path;    public Node(int index) {        this.index  = index;        this.path = new LinkedList<>();        path.add(index);    }    public Node(int index, List<Integer> path) {        this.index = index;        this.path = new LinkedList<>(path);        path.add(index);    }}

1.5 拓扑排序

1.5.1 判断有向图是否存在环

207. 课程表

看到依赖问题，首先想到的就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循环依赖。

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

输入：numCourses = 2, prerequisites = [[1,0]]输出：true解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。输入：numCourses = 2, prerequisites = [[1,0],[0,1]]输出：false解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

public class BuildGraph {
    boolean[] visited;//用来标记节点是否访问过
    boolean[] onPath;//用来标记当前遍历的路径上是否已经有该节点了，有就代表这条路径上有环
    boolean flag=false;//是否有环的标志位
    
    public boolean canFinish(int numCourses, int[][] prerequisites){
        visited = new boolean[numCourses];
        onPath = new boolean[numCourses];
//        1.根据输入构造图的线性表结构
        List<Integer>[] graph = buildGraph(numCourses,prerequisites);
//        2.遍历图结构,因为可能存在课程是孤立的所有采用for循环去遍历所有节点
        for (int i = 0; i < numCourses; i++) {
            traverse(graph,i);
        }
        return !flag;
    }
    
    public List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = new LinkedList[numCourses];
//        1.初始化！非常重要，不然会报 NullPointException;
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new LinkedList<>();
        }
        for (int[] edge : prerequisites) {
            int from = edge[1];
            int to = edge[0];
            graph[from].add(to);
        }
        return graph;
    }
    
    public void traverse(List<Integer>[] graph,int node){//遍历当前节点，如果已经访问过就直接返回
//        1.先判断当前节点是否已经在路径上
        if (onPath[node]) {
            flag=true;
        }
//        2.判断当前节点是否已经遍历过
        if(visited[node]){
            return ;
        }
//        3.如果没有，就将当前节点的状态改为已遍历,并加入当前遍历路径上
        visited[node] = true;
        onPath[node] =true;
//        4.遍历当前节点的所有相关的节点
        for (Integer t : graph[node]) {
            traverse(graph,t);
        }
//        5.遍历完一样需要回退节点
        onPath[node] = false;
    }
}

1.5.2 输出拓扑顺序：深度遍历法

——将后序遍历的结果进行反转，就是拓扑排序的结果

直观地说就是，让你把一幅图「拉平」，而且这个「拉平」的图里面，所有箭头方向都是一致的

210. 课程表 II

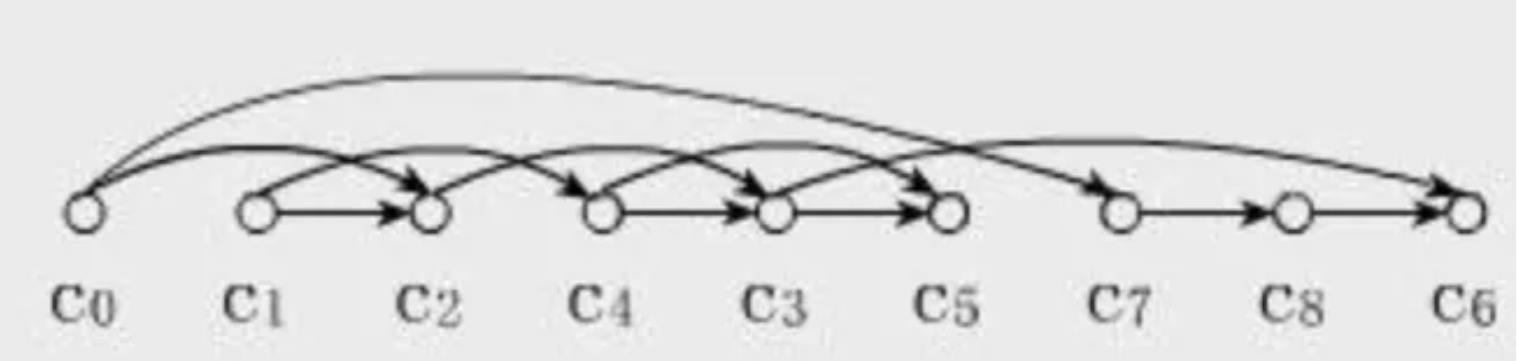
不仅要判断是否能修完所有课程，并且如果能的话还要输出上课的顺序结果

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

	ArrayList<Integer> list = new ArrayList<>();
    public int[] findOrder(int numCourses, int[][] prerequisites){
//        1.如果输入成环的话，直接就没有
        if(!canFinish(numCourses,prerequisites)){
            return new int[]{};
        }
//        2.建图
        List<Integer>[] graph = buildGraph(numCourses, prerequisites);
//        3.深度遍历图
        visited = new boolean[numCourses];
        for (int i = 0; i < numCourses; i++) {
            traverseOrder(graph,i);
        }
//        4.反转遍历结果
        Collections.reverse(list);
        int[] ans = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ans[i] = list.get(i);
        }
        return ans;

    }

//	后续遍历
    public void traverseOrder(List<Integer>[] graph,int node){
//        1.判断当前节点是否已经遍历过
        if(visited[node]){
            return ;
        }
//        2.如果没有，就将当前节点的状态改为已遍历
        visited[node] = true;
//        3.遍历当前节点的所有相关的节点
        for (Integer t : graph[node]) {
            traverseOrder(graph,t);
        }
        list.add(node);
    }

	public boolean canFinish(int numCourses, int[][] prerequisites){}

1.5.3 拓扑排序：广度优先遍历法

210. 课程表 II

不仅要判断是否能修完所有课程，并且如果能的话还要输出上课的顺序结果

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

拓扑排序的作用：

1、得到一个「拓扑序」,「拓扑序」不唯一；

2、检测「有向图」是否有环。

算法流程：

1、在开始排序前，扫描对应的存储空间（使用邻接表），将入度为 0 的结点放入队列。

2、只要队列非空，就从队首取出入度为 0 的结点，将这个结点输出到结果集中，并且将这个结点的所有邻接结点的入度减 1，在减 1 以后，如果这个被减 1 的结点的入度为 0 ，就继续入队。

3、当队列为空的时候，检查结果集中的顶点个数是否和课程数相等。

public int[] findOrder(int numCourses, int[][] prerequisites) {
//        1.创建节点的线性表，防止重复，用HashSet
        HashSet<Integer>[] graph = new HashSet[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new HashSet<>();
        }
//        2.将节点信息添加到set中
//        3.维护所有节点的入度
        int[] deep = new int[numCourses];
        for (int[] edge : prerequisites) {
            int from = edge[1];
            int to = edge[0];
            graph[from].add(to);
            deep[to]++;
        }
//        4.把所有度为0的节点入队列
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if(deep[i]==0){
                queue.offer(i);
            }
        }
//        5.创建结果集
        int[] res = new int[numCourses];
        int count=0;
//        6.不断删除度为0的节点,将节点入结果集并更新其后继的度
        while(!queue.isEmpty()){
            Integer node = queue.poll();
            res[count++] = node;
            for (Integer next : graph[node]) {
                deep[next]--;
                if(deep[next]==0){
                    queue.offer(next);
                }
            }
        }
        if(count!=numCourses){
            return new int[]{};
        }else{
            return res;
        }
    }

2 真题

2.1 路径问题（动态规划）

推荐好文章，代码非常合我心意：https://www.jianshu.com/p/524979bde668

2.1.1 64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→以上是关于一文通数据结构与算法之——图+常见题型与解题策略+Leetcode经典题的主要内容，如果未能解决你的问题，请参考以下文章
 

 一文通数据结构与算法之——数组+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——贪心算法+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——回溯算法+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——二叉树+常见题型与解题策略+Leetcode经典题


 一网打尽！二分查找解题模版与题型全面解析


 Python数据结构与算法篇-- 链表的应用与常见题型